やりなおしの数学・微分積分篇（58/X） - 「大人の教養・知識・気付き」を伸ばすブログ

　以下の書籍を参考に、改めて微分積分を復習していく。

理工系のための微分積分〈2〉

作者:武, 鈴木,良弘, 柴田,和永, 田中,義雄, 山田
内田老鶴圃

Amazon

前回

power-of-awareness.com

前回
今日のまとめ
10.　ベクトル解析
- 10.3　曲面の曲面積と関数の線積分・面積分
  - 10.3.3　ベクトル値関数の線積分・面積分
次回

今日のまとめ

ベクトル値関数の線積分・面積分を定義し、実際に計算してみる。

10.　ベクトル解析

　本節ではベクトル値写像を扱う。

10.3　曲面の曲面積と関数の線積分・面積分

10.3.3　ベクトル値関数の線積分・面積分

　ベクトル値関数 $\boldsymbol{V}(\boldsymbol{x})$ における線積分および面積分を扱う。

　 $n=2,3$ として $C\subset\mathbb{R}^n$ を曲線とし、 $C$ 上の点 $\boldsymbol{p}$ に対して単位接ベクトル $\boldsymbol{t}=\boldsymbol{t}(\boldsymbol{p})$ を $\boldsymbol{p}\mapsto\boldsymbol{t}(\boldsymbol{p})$ が連続となるように選ぶ。このとき $C$ の近傍で与えられたベクトル値関数 $\boldsymbol{V}(\boldsymbol{x})$ に対して積分 $\displaystyle{\int_C(\boldsymbol{V},\boldsymbol{t})}dl$ を計算する。
　写像 $\boldsymbol{\gamma}:[a,b]\rightarrow\mathbb{R}^n$ により $C=\{\boldsymbol{\gamma}(\tau)|\tau\in[a,b]\}$ とパラメータ表示できるものと仮定する。このとき $\boldsymbol{\gamma}^{\prime}$ は $\boldsymbol{0}$ でない接ベクトルであるから、

$\begin{aligned} \boldsymbol{t}=\pm\displaystyle{\frac{\boldsymbol{\gamma}^{\prime}}{|\boldsymbol{\gamma}^{\prime}|}} \end{aligned}$

が成り立つ。これを踏まえて計算すれば

$\begin{aligned} \displaystyle{\int_C(\boldsymbol{V},\boldsymbol{t})}dl&=\displaystyle{\int_a^b\left(\boldsymbol{V}(\boldsymbol{\gamma}(\tau),\pm\displaystyle{\frac{\boldsymbol{\gamma}^{\prime}}{|\boldsymbol{\gamma}^{\prime}|}}\right)\left|\boldsymbol{\gamma}^{\prime}\right|d\tau}\\ &=\pm\displaystyle{\int_a^b\left(\boldsymbol{V}(\boldsymbol{\gamma}(\tau),\boldsymbol{\gamma}^{\prime}\right)d\tau} \end{aligned}$

が得られる。したがって $C$ のパラメータ付け $\displaystyle{\gamma}^{\prime}$ の向きと $\boldsymbol{t}$ の方向が一致する場合、

$\begin{aligned} \displaystyle{\int_C(\boldsymbol{V},\boldsymbol{t})}dl=\displaystyle{\int_a^b\left(\boldsymbol{V}(\boldsymbol{\gamma}(\tau),\boldsymbol{\gamma}^{\prime}\right)d\tau}=\displaystyle{\int_a^b \sum_{i=1}^{n}V_i(\boldsymbol{\gamma}(\tau))\gamma_i^{\prime}} d\tau \end{aligned}$

が成り立つ。

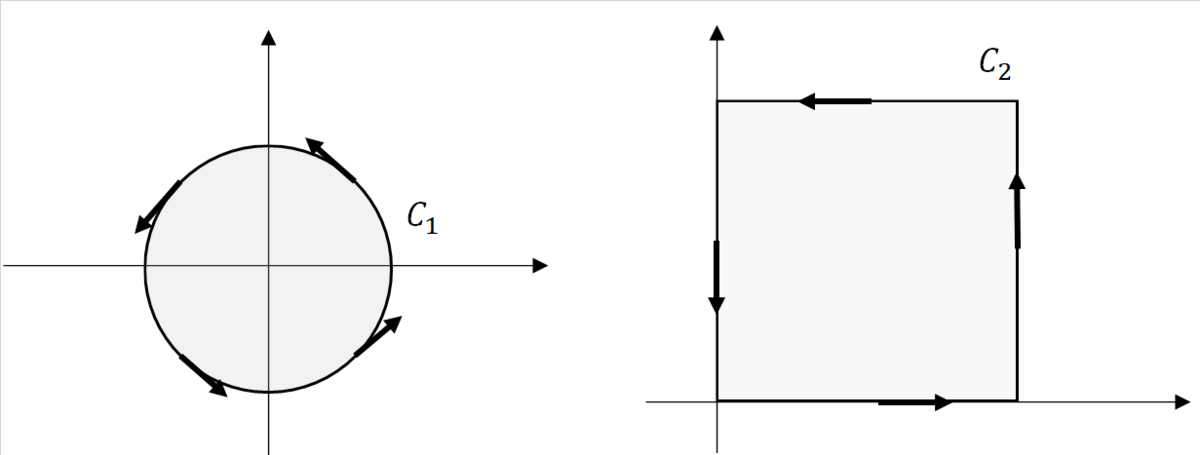
計算例
　 $C_1=\{(x,y)|x^2+y^2=1\}$ とし、 $C_2$ を $[0,1]\times[0,1]$ の外周とする。 $C_1,C_2$ 上の単位ベクトルを2次元座標平面上で以下の図のように取る。
このときに $\boldsymbol{V}(x,y)=\begin{bmatrix}-y\\x\end{bmatrix}$ に対して $\boldsymbol{\int_{C_i}(\boldsymbol{V},\boldsymbol{t})}dl,i=1,2$ を求める。
　まず $C_1$ が $\boldsymbol{\gamma}(\tau)=\begin{bmatrix}\cos\tau\\\sin\tau\end{bmatrix},\tau\in[0,2\pi)$ と書けることから、

$\begin{aligned} \boldsymbol{\int_{C_1}(\boldsymbol{V},\boldsymbol{t})}dl&=\displaystyle{\int_0^{2\pi}\left\{(-\sin\tau)(\cos\tau)^{\prime}+(\cos\tau)(\sin\tau)^{\prime}\right\}d\tau}\\ &=\displaystyle{\int_0^{2\pi}d\tau}\ (\because\ \cos^2\tau+\sin^2\tau=1)\\ &=2\pi \end{aligned}$

である。
　次に $C_2$ について、4つの部分 $(0,0)\rightarrow(1,0),$ $(1,0)\rightarrow(1,1),$ $(1,1)\rightarrow(0,1),$ $(0,1)\rightarrow(0,0)$ に分ける。これらをそれぞれ $\tau\mapsto(\tau,0),$ $\tau\mapsto(1,\tau),$ $\tau\mapsto(1-\tau,1),$ $\tau\mapsto(0,1-\tau),0\leq\tau\leq1$ とパラメータ表示できることから、

$\begin{aligned} \boldsymbol{\int_{C_2}(\boldsymbol{V},\boldsymbol{t})}dl=&\boldsymbol{\int_{0}^{1}\left(\begin{bmatrix}0\\\tau\end{bmatrix},\begin{bmatrix}1\\0\end{bmatrix}\right)}d\tau+\boldsymbol{\int_{0}^{1}\left(\begin{bmatrix}-\tau\\1\end{bmatrix},\begin{bmatrix}0\\1\end{bmatrix}\right)}d\tau\\ &+\boldsymbol{\int_{0}^{1}\left(\begin{bmatrix}-1\\1-\tau\end{bmatrix},\begin{bmatrix}-1\\0\end{bmatrix}\right)}d\tau+\boldsymbol{\int_{0}^{1}\left(\begin{bmatrix}-(1-\tau)\\0\end{bmatrix},\begin{bmatrix}0\\-1\end{bmatrix}\right)}d\tau\\ =&2\displaystyle{\int_0^1}d\tau\\ =&2 \end{aligned}$

である。

　次に面積分を考える。 $\mathbb{R}^3$ において表裏を考えられる有界な曲面 $S\subset\mathbb{R}^3$ 上での積分を考える。 $S$ 上の表向きの単位法ベクトルを $\boldsymbol{n}$ とし、これを正の向きの単位法ベクトルと呼ぶ。 $S$ の近傍において定義された $\mathbb{R}^3$ 値関数 $\boldsymbol{V}(\boldsymbol{x})$ に対して積分 $\boldsymbol{\iint_{S}(\boldsymbol{V},\boldsymbol{n})}d\sigma$ を計算したい。
　 $D\subset\mathbb{R}^2$ を有界閉領域とし $\boldsymbol{\gamma}(s,t):D\rightarrow\mathbb{R}^3$ により $S=\{\boldsymbol{\gamma}(s,t)|(s,t)\in D\}$ とパラメータ表示されているものとする。 $\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t$ は $S$ の法ベクトルであるから、

$\begin{aligned} \boldsymbol{n}=\pm\displaystyle{\frac{\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t}{\left|\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t\right|}} \end{aligned}$

が成り立つ。したがって

$\begin{aligned} \displaystyle{\iint_S (\boldsymbol{V},\boldsymbol{n})}d\sigma&=\displaystyle{\iint_D\left(\boldsymbol{V}(\boldsymbol{\gamma}(s,t)),\pm\displaystyle{\frac{\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t}{\left|\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t\right|}}\right)}\left|\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t\right|dsdt\\ &=\pm\displaystyle{\iint_D\left(\boldsymbol{V}(\boldsymbol{\gamma}(s,t)),\boldsymbol{\gamma}_s\times\boldsymbol{\gamma}_t\right)}dsdt\\ &=\pm\displaystyle{\iint_D\left(V_1(\boldsymbol{\gamma})\displaystyle{\frac{\partial(\gamma_2,\gamma_3)}{\partial(s,t)}}+V_2(\boldsymbol{\gamma})\displaystyle{\frac{\partial(\gamma_3,\gamma_1)}{\partial(s,t)}}+V_3(\boldsymbol{\gamma})\displaystyle{\frac{\partial(\gamma_1,\gamma_2)}{\partial(s,t)}}\right)}dsdt \end{aligned}$

が成り立ち、また実数値関数 $f(\boldsymbol{x}):D\rightarrow\mathbb{R}$ に対して

$\begin{aligned} \displaystyle{\iint_S f(\boldsymbol{x})n_1}d\sigma&=\pm\displaystyle{\iint_D f(\boldsymbol{\gamma})\frac{\partial(\gamma_2,\gamma_3)}{\partial(s,t)}}dsdt,\\ \displaystyle{\iint_S f(\boldsymbol{x})n_2}d\sigma&=\pm\displaystyle{\iint_D f(\boldsymbol{\gamma})\frac{\partial(\gamma_3,\gamma_1)}{\partial(s,t)}}dsdt,\\ \displaystyle{\iint_S f(\boldsymbol{x})n_3}d\sigma&=\pm\displaystyle{\iint_D f(\boldsymbol{\gamma})\frac{\partial(\gamma_1,\gamma_2)}{\partial(s,t)}}dsdt \end{aligned}$

も成立する。符号は $\boldsymbol{\gamma}_{s}\times\boldsymbol{\gamma}_{t}$ と $\boldsymbol{n}$ が同じ向きを持つとき、正となる。このとき $\boldsymbol{\gamma}(s,t)$
は $S$ の正のパラメータ付けという。

計算例
　 $S$ を円柱 $\mathit{\Omega}=\{(x,y,z)|x^2+y^2\leq1,0\leq z\leq1\}$ の側面だとし、その単位法ベクトルを外向きに取る。 $\boldsymbol{V}(x,y,z)=\begin{bmatrix}x\\y\\-z\end{bmatrix}$ とするとき $\displaystyle{\iint_S(\boldsymbol{V},\boldsymbol{n})}d\sigma$ を考える。
　 $S$ は $\boldsymbol{\gamma}(\theta,t)=\begin{bmatrix}\cos\theta\\\sin\theta\\t\end{bmatrix},\theta\in[0,2\pi),t\in[0,1]$ とおけば、 $\boldsymbol{\gamma}(\theta,t)$ での $S$ の外向き単位法ベクトルは $\boldsymbol{n}=\begin{bmatrix}\cos\theta\\\sin\theta\\0\end{bmatrix}$ で与えられる。

$\begin{aligned} \boldsymbol{\gamma}_{\theta}\times\boldsymbol{\gamma}_{t}&=\begin{bmatrix}-\sin\theta\\\cos\theta\\0\end{bmatrix}\times \begin{bmatrix}0\\0\\1\end{bmatrix}\\ &=\begin{bmatrix}\cos\theta\\\sin\theta\\0\end{bmatrix} \end{aligned}$

と $\boldsymbol{n}$ と同じ方向を持つから、

$\begin{aligned} \displaystyle{\iint_S(\boldsymbol{V},\boldsymbol{n})}d\sigma&=\displaystyle{\iint_{[0,2\pi]\times[0,1]}(\boldsymbol{V}(\boldsymbol{\gamma}(\theta,t)),\boldsymbol{\gamma}_{\theta}\times\boldsymbol{\gamma}_{t})}d\theta dt\\ &=\displaystyle{\iint_{[0,2\pi]\times[0,1]}\left(\begin{bmatrix}\cos\theta\\\sin\theta\\-2t\end{bmatrix},\begin{bmatrix}\cos\theta\\\sin\theta\\0\end{bmatrix}\right)}d\theta dt\\ &=\displaystyle{\iint_{[0,2\pi]\times[0,1]}}d\theta dt\ (\because\ \sin^2\theta+\cos^2\theta=1)\\ &=\displaystyle{\int_{[0,2\pi]}}d\theta\\ &=2\pi \end{aligned}$

である。