証券投資論（08/21） - 「大人の教養・知識・気付き」を伸ばすブログ

　証券投資（現代ポートフォリオ理論）をコンパクトに学ぶべく、比較的最近に発刊され薄めの本である

証券投資理論 (Minervaファイナンス講座)

作者:八木恭子,澤木勝茂
ミネルヴァ書房

Amazon

を参考に学んでいく。

3.　ポートフォリオ理論
- 3.7.　無リスク資産を含むポートフォリオ
- 3.8　平均=分散モデルの問題点

前回：

power-of-awareness.com

3.　ポートフォリオ理論

3.7.　無リスク資産を含むポートフォリオ

　無リスク証券が存在するとして、無リスク資産を組み入れたポートフォリオを考える。このときの最適ポートフォリオとして

$\begin{aligned} \boldsymbol{\omega}^{*}&=\lambda V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})\\ &=V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})\displaystyle{\frac{E[r_P]-r_0}{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}},\\ x_0^{*}&=1-{}^{t}\boldsymbol{1}\boldsymbol{\omega}^{*} \end{aligned}$

が得られる。
　これを代入することでポートフォリオ $P$ の分散は

$\begin{aligned} V[r_P]&={}^{t}\boldsymbol{x}^{*}V\boldsymbol{x}^{*}\\ &={}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}V\left(\displaystyle{\frac{E[r_P]-r_0}{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}}\right)^2V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})\\ &={}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})\left(\displaystyle{\frac{E[r_P]-r_0}{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}}\right)^2\\ &=\displaystyle{\frac{(E[r_P]-r_0)^2}{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}} \end{aligned}$

である。すなわち $(V[r_P],E[r_P])$ 平面では放物線を描き、 $(\sigma[r_P],E[r_P])$ 平面では $E[r_P]$ 軸上の切片を $r_0$ とした傾き $\pm\sqrt{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}$ の半直線を描く。

無リスク証券を含めた場合の $(\sigma[r_P],E[r_P])$ 平面上の
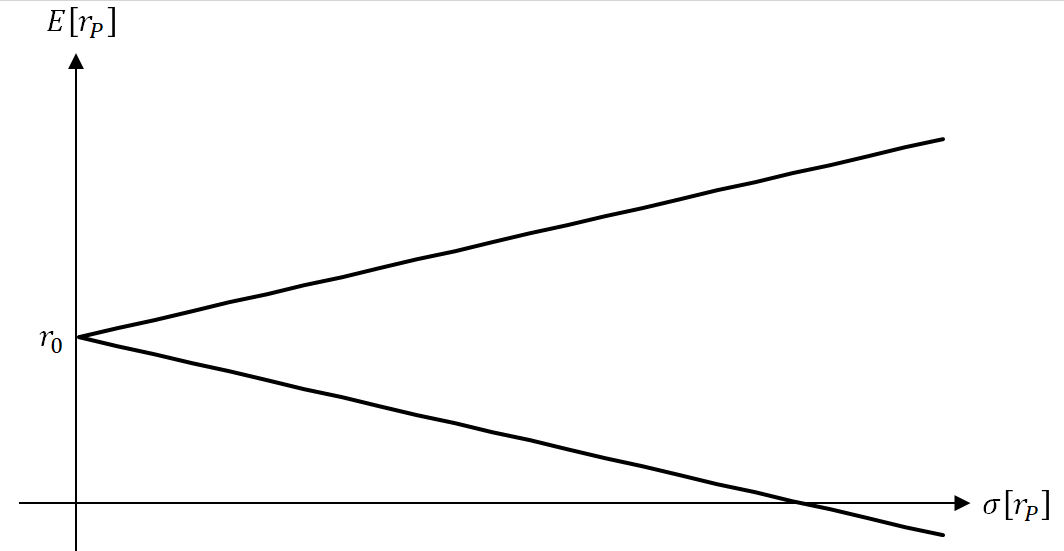
最小分散ポートフォリオ f:id:suguru_125:20220214025351p:plain

　すなわち

$\begin{aligned} E[r_P]-r_0=\begin{cases} &\sqrt{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}\sqrt{V[r_P]},&E[r_P]\geq r_0,\\ &-\sqrt{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}\sqrt{V[r_P]},&E[r_P]\lt r_0 \end{cases} \end{aligned}$

である。
　リスク証券からのみ構成されるポートフォリオと同様に効率的ポートフォリオは点 $(0,r_0)$ を切片とした傾き $\pm\sqrt{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}$ を持つ半直線からなる。

　無リスク証券を含む効率的ポートフォリオおよびリスク証券のみからなる効率的ポートフォリオとを組み合わせたときにどのような議論が成り立つか。
　リスク証券のみからなる効率的ポートフォリオは双曲線であり、特に

$\begin{aligned} r_0=\displaystyle{\frac{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}} \end{aligned}$

である場合、

$\begin{aligned} {}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})&={}^{t}\boldsymbol{\mu}V^{-1}\boldsymbol{\mu}-2{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu} r_0+{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}r_0^2\\ &={}^{t}\boldsymbol{\mu}V^{-1}\boldsymbol{\mu}-2{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}\left(\displaystyle{\frac{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}}\right)+{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}\left(\displaystyle{\frac{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}}\right)^2\\ &=\displaystyle{\frac{{}^{t}\boldsymbol{\mu}V^{-1}\boldsymbol{\mu}{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-\left({}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}\right)^2}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}}\gt0 \end{aligned}$

となり、半直線 $E[r_P]=\displaystyle{\frac{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}}\pm\displaystyle{\sqrt{\displaystyle{\frac{{}^{t}\boldsymbol{\mu}V^{-1}\boldsymbol{\mu}{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-\left({}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}\right)^2}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}}}}\sqrt{V[r_P]}$ はリスク証券のみからなる効率的ポートフォリオの漸近線になる。
　このとき最適ポートフォリオ $\boldsymbol{x}^{*}$ は

$\begin{aligned} {}^{t}\boldsymbol{1}\boldsymbol{x}^{*}&={}^{t}\boldsymbol{1}V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1}) \displaystyle{\frac{E[r_P]-r_0}{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}}\\ &=\left({}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-\displaystyle{\frac{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}}\cdot{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}\right)\left(\displaystyle{\frac{E[r_P]-r_0}{{}^{t}(\boldsymbol{\mu}-r_0\boldsymbol{1})V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1})}}\right)\\ &=0 \end{aligned}$

となるから、 $x_0^{*}=1$ となり、最適ポートフォリオは無リスク証券への集中投資である。
　リスク証券への投資比率の合計は $0$ であるから、これは自己資産 $0$ でポートフォリオを形成するという意味で最低ポートフォリオを保有することを意味する。
　以上の考察をまとめる：

無リスク証券を含むポートフォリオ　無リスク証券およびリスク証券からなるポートフォリオにおいて $\sqrt{{V}[r_P]},E[r_P]$ 平面上の効率的フロンティアは $E[r_P]=r_0$ を切片とする2本の半直線として得られる。
　 $A={}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}, C={}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}$ としたとき、 $r_0\neq\displaystyle{\frac{A}{C}}$ ならば接点ポートフォリオおよび無リスク証券から成るポートフォリオはまた効率的ポートフォリオになる。
　 $r_0=\displaystyle{\frac{A}{C}}$ ならば、無リスク証券および裁定ポートフォリオ $\boldsymbol{x}_0^{*}={}^{t}(x_{0,1}^{*},\cdots,x_{0,n}^{*})\ s.t.\ \displaystyle{\sum_{i=1}^{n}x_{0,i}^{*}}=0$ とを組み合わせたポートフォリオは効率的フロンティア上に生成可能だが、無リスク証券および接点ポートフォリオとの組み合わせではその効率的フロンティア上のポートフォリオを組成できない。

　この命題から、接点ポートフォリオが存在する場合、任意の効率的ポートフォリオは接点ポートフォリオおよび無リスク証券の一次結合で表現できるから、効率的ポートフォリオおよび接点ポートフォリオは完全相関の関係にある。

接点ポートフォリオおよび無リスク証券からなる効率的ポートフォリオのリスク・リターン　無リスク証券があるとき、任意の効率的ポートフォリオを $P$ とし、無リスク証券のリターンを $r_0$ と効率的ポートフォリオ $P$ のリターンとの間には、リスク証券 $j$ のリターンを $r_j$ とすれば

$\begin{aligned} E[r_j]&=r_0+\beta_j^{P}\left(E[r_P]-r_0\right),\\ \beta_j^{P}&=\displaystyle{\frac{\mathrm{Cov}[r_j,r_P]}{V[r_P]}} \end{aligned}$

を満たす。

( $\because$ 　リスク証券 $j$ からなるポートフォリオ $\boldsymbol{x}^{j}={}^{t}(0,\cdots,1^{j},\cdots,0)$ ( $1^{j}$ は左記ベクトルの第 $j$ 成分が $1$ であることを意味する。)とし、 $\boldsymbol{x}_{T}$ を接点ポートフォリオとしたとき

$\begin{aligned} \mathrm{Cov}[r_j,r_P]={}^{t}\boldsymbol{x}^{j}V\boldsymbol{x}_T \end{aligned}$

である。このとき

$\begin{aligned} \mathrm{Cov}[r_j,r_P]&=(1-\theta)\mathrm{Cov}[r_j,r_T],\\ \theta&=\displaystyle{\frac{E[r_T]-E[r_P]}{E[r_T]-r_0}} \end{aligned}$

を踏まえると、あるポートフォリオ $P$ の各リスク証券との共分散ベクトルを $\sigma_{\cdot j}[r_P]=V\boldsymbol{x}_P$ とすれば

$\begin{aligned} \sigma_{\cdot j}[r_P]=(1-\theta)\sigma_{\cdot j}[r_T] \end{aligned}$

である。接点ポートフォリオは

$\begin{aligned} \boldsymbol{x}_{T}=\displaystyle{\frac{1}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-r_0{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}}V^{-1}(\boldsymbol{\mu}-r_0\boldsymbol{1}) \end{aligned}$

であるから、これを代入して

$\begin{aligned} \sigma_{\cdot j}[r_P]=(1-\theta)V\boldsymbol{x}_T=\displaystyle{\frac{1-\theta}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-r_0{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}}(\boldsymbol{\mu}-r_0\boldsymbol{1}) \end{aligned}$

を得る。これを $\boldsymbol{\mu}$ について解くことで

$\begin{aligned} (\boldsymbol{\mu}-r_0\boldsymbol{1})=\displaystyle{\frac{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-r_0{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}}{1-\theta}}(\boldsymbol{\mu}-r_0\boldsymbol{1}) \end{aligned}$

を得る。
　一方で効率的ポートフォリオ $P$ のリターンの分散は、

$\begin{aligned} V[r_T]&={}^{t}\boldsymbol{x}_TV\boldsymbol{x}_T\\ &=\displaystyle{\frac{E[r_T]-r_0}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}r_0}} \end{aligned}$

を踏まえれば、

$\begin{aligned} V[r_P]&=(1-\theta)^2V[r_T]\\ &=(1-\theta)^2\displaystyle{\frac{E[r_T]-r_0}{{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{\mu}-{}^{t}\boldsymbol{1}V^{-1}\boldsymbol{1}r_0}} \end{aligned}$

である。 $\boldsymbol{1}V^{-1}\boldsymbol{\mu}-\boldsymbol{1}V^{-1}\boldsymbol{1}r_0=(1-\theta)^2\displaystyle{\frac{E[r_T]-r_0}{V[r_P]}}$ を代入して

$\begin{aligned} \boldsymbol{\mu}_-r_0\boldsymbol{1}&=\displaystyle{\frac{(1-\theta)(E[r_T]-r_0)}{V[r_P]}}\sigma_{\cdot j}[r_P]\\ &=\displaystyle{\frac{\sigma_{\cdot j}[r_{P}]}{V[r_P]}}(E[r_P]-r_0) \end{aligned}$

を得る。 $\displaystyle{\frac{\sigma_{\cdot j}[r_{P}]}{V[r_P]}}$ の第 $j$ 番目の要素は $\displaystyle{\frac{\mathrm{Cov}[r_j,r_P]}{V[r_P]}}$ に等しいから、示すべき式を得る。　 $\blacksquare$ )