「大人の教養・知識・気付き」を伸ばすブログ

一流の大人（ビジネスマン、政治家、リーダー…）として知っておきたい、教養・社会動向を意外なところから取り上げ学ぶことで“気付く力”を伸ばすブログです。データ分析・語学に力点を置いています。　→現在、コンサルタントの雛になるべく、少しずつ勉強中です(※2024年1月21日改訂)。

MENU

内部収益率（IRR）を確認しよう

企業価値評価 金融・ファイナンス

はじめに

　内部収益率（IRR）がわからないという声に対して、

と解答しました。内部収益率は普段使わず少し考え込んでしまったので、これを機にあらためて内部収益率が何なのかを整理してみようと思います。

今日のまとめ

  • 内部収益率（Internal Rate of Return）は、投資案件の正味現在価値(NPV)を0にするような割引率と定義。
  • 言い換えると、内部収益率は、キャッシュフローが発生する時点や金額が各々異なる投資案件を、それと経済的に等価な、期初にだけキャッシュを投資し満期にキャッシュを得る案件に直したとき、当該案件が何%の利率に相当するかに直したもの。
  • 利率に変えることで、期間の相違を考慮しつつ、その投資プロジェクトの“良さ”を評価可能。

目次

1.　まずは形式的な定義を

　内部収益率（Internal Rate of Return）は、投資案件の正味現在価値(NPV)を0にするような割引率です。

2.　現在価値について理解している？

　内部収益率は現在価値の概念で定義される以上、現在価値(Present value)を理解していないといけません。株式、投資プロジェクト、貸出……。何でもよいのですが、現金を生み出す（もしくは現金を投資しないといけない）ものの経済的価値を評価するために求めるのが現在価値です。ここでは簡便のため、投資プロジェクトを扱いましょう。
　さて、投資プロジェクトは、現金を生み出すこともあれば支出しないといけないこともあります。収益なのか支出なのかという点で、①方向性（プラス・マイナス）があります。また②金額の大きさもあります。さらには、そうした収益・支出が③いつ発生するか（発生時点）を考えることもまた必要です。一般に、方向性を考えた、ある金額の大きさをもつ現金をキャッシュフローと呼びます。

　ここで問題になるのが③です。すなわち、ある時点で発生する収益と、それよりも後に発生するが同額な収益は、価値が同じでしょうか？答えは否です。一般に、回収できるタイミングに応じて価値は異なると考えます。なぜならば、もしもある金額を今得られるのか、もしくはそれと同額を1年後に得られるのであれば、今その金額を得て銀行預金にすれば、（今は微々たる額ですが）利息が得られるために前者の方がより大きな額を得られるからです。もっといえば、そもそも1年後にはその金額を得られない恐れもあります。このように、利殖性や、回収可能性などのリスクが原因となって、期間が異なる同額のキャッシュは価値が異なると考えます。
　逆に言えば、リスクも織り込んだ利息を考慮すれば、ある時点に発生するキャッシュフローに対し、経済的価値の面で等価だが異なる時点に発生するキャッシュフローを考えることができます。これが現在価値の考え方です。

　数式で考えましょう。簡単のため、常に利率rで運用できるという前提で、ある時点t=t\gt0に発生するキャッシュフローCF_tは、現在時点t=0に得られる金額としていくつに相当するかを考えます。このとき、その金額をPVと書くと、

\begin{aligned} PV=\displaystyle{\frac{CF_t}{(1+r)^t}} \end{aligned}

で表されます。ここまでが分かれば、現在価値は十分に分かったと言えます。
　投資プロジェクトを考えるには、そのプロジェクトがもたらすすべてのキャッシュフロー（キャッシュインもキャッシュアウトも）の現在価値を算出し、それら全部を合算したものが正味現在価値(Net Present Value)です*1。
　さて、内部収益率の理解において重要なのは、すでに述べたことの繰り返しではありますが、現在価値の世界では、発生時点も金額も異なるキャッシュフローであっても、現在価値が等しいのであれば、それらのキャッシュフローはすべて等価（＝同じもの）として扱うということです。

3.　内部収益率を簡単な例で考えてみましょう

　簡単のために、2つの投資プロジェクトを内部収益率で比較してみましょう。

　具体的なキャッシュフローは以下のように毎年発生するとします（簡単のため、以下のキャッシュフローは確実に発生するものとします）。

t=0 1 2
-100 12.5 112.5
  • プロジェクトB：3年かけて資金を回収するプロジェクト

　具体的なキャッシュフローは以下のように毎年発生するとします（簡単のため、以下のキャッシュフローは確実に発生するものとします）。

t=0 1 2 3
-100 10 10 105

これらは、現在価値を考慮しなければ、得られる金額はともに25で等しいです。
　もしこれらを正味現在価値で評価する場合、各プロジェクトに適用する割引率が分からないといけません。ここでは、それらを考えずに内部収益率で考えてみましょう。
　プロジェクトA,Bの内部収益率をそれぞれr_A,r_Bだと設定します。すると、

\begin{aligned} NPV_{A}&=\displaystyle{\frac{12.5}{1+r_A}}+\displaystyle{\frac{112.5}{(1+r_A)^2}}-100=0\\ NPV_{B}&=\displaystyle{\frac{10}{1+r_B}}+\displaystyle{\frac{10}{(1+r_B)^2}}+\displaystyle{\frac{105}{(1+r_B)^3}}-100=0 \end{aligned}

が成り立つはずです。
　これらを整理すると、

\begin{aligned} 100(1+r_A)^2-12.5(1+r_A)-112.5&=0\\ 100(1+r_B)^3-10(1+r_B)^2-10(1+r_B)-105&=0 \end{aligned}

が得られます。これらはそれぞれ2次方程式、3次方程式の解を求めればよく、最終的に、r_A=12.50\%,r_B=8.47\%が得られます。この結果から、プロジェクトAの方が利率が高く望ましいプロジェクトだと言えます。

補足：数式でしっかりと議論しておくと…

　ある投資案件Iが、キャッシュインを時点t=t_1,t_2,\cdots,t_k(t_1\lt t_2\lt t_k)にそれぞれCIF_{t}(\gt0)だけ、またキャッシュアウトをt=s_1,s_2,\cdots,s_l(s_1\lt s_2\lt s_l)にそれぞれCOF_{t}(COF_{t}\gt0)だけ発生するとする。また、本案件の割引率をrとする。

　内部収益率rは、正味現在価値が0になるような割引率であった。そこで、この案件では、

\begin{align} \displaystyle{\sum_{i=1}^{l}\frac{COF_{s_i}}{(1+r)^{s_i}}}+\displaystyle{\sum_{j=1}^{k}\frac{CIF_{t_j}}{(1+r)^{t_j}}}\equiv0\tag{1} \end{align}

が成り立つはずである。ここで左辺第1項はキャッシュアウトの現在価値で、同第2項はキャッシュインの現在価値である。
　式(1)はいったん置いておき、この案件を、初期時点(t=0)に一括投資し、満期（ここではt=t_kを満期とする。）に一括してキャッシュインがあるという形式にキャッシュフローを引き直してみる。


初期時点にキャッシュアウト、満期にキャッシュインを引き直すイメージ

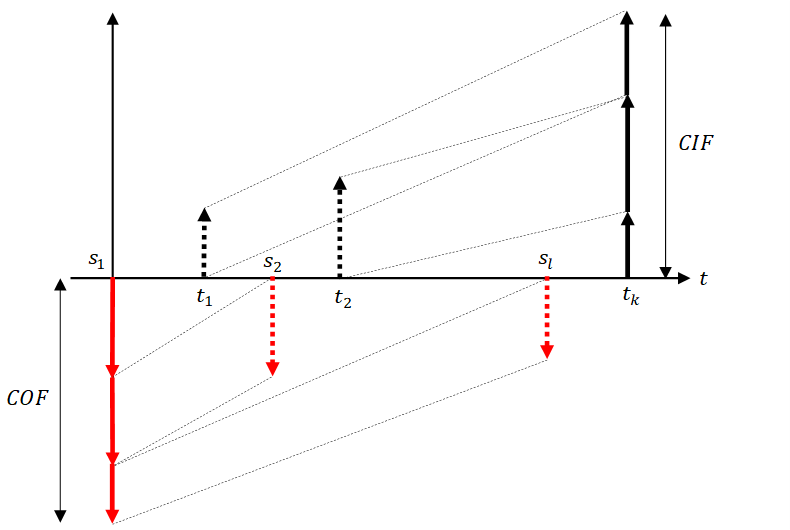
　すると、初期時点に引き直したキャッシュアウトの合算値COF（これは定義から現在価値である）は、

\begin{align} COF=\displaystyle{\sum_{i=1}^{l}\frac{COF_{s_i}}{(1+r)^{s_i}}} \tag{2} \end{align}

と書ける。また、満期時点に引き直したキャッシュインの合算値CIFのt=t_kにおける将来価値は、

\begin{align} CIF=\displaystyle{\sum_{j=1}^{k}(1+r)^{t_k-t_j}CIF_{t_j}}=\displaystyle{\sum_{j=1}^{k}\frac{CIF_{t_j}}{(1+r)^{t_j-t_k}}} \tag{3} \end{align}

と書ける。
　さて、式(1)に式(2)を代入すれば、

\begin{align} \displaystyle{\sum_{j=1}^{k}\frac{CIF_{t_j}}{(1+r)^{t_j}}}\equiv-COF \end{align}

を得るが、式(3)に代入すれば、

\begin{align} CIF&=\displaystyle{\sum_{j=1}^{k}(1+r)^{t_k-t_j}CIF_{t_j}}=\displaystyle{\sum_{j=1}^{k}\frac{CIF_{t_j}}{(1+r)^{t_j-t_k}}}\\ &=(1+r)^{t_k}\displaystyle{\sum_{j=1}^{k}\frac{CIF_{t_j}}{(1+r)^{t_j}}}\\ &=-(1+r)^{t_k}COF \end{align}

を得る。これは、初期時点に|COF|だけ投資して利率rで複利運用した場合、最終時点にはCIFだけ得られるということに他ならない。すなわち、内部収益率は、キャッシュインとキャッシュアウトがある投資案件を、それと経済的に等価な、初期時点でのみ一定額を投資して満期に一括してある額だけ得られる投資案件における年利に相当するのである。

*1:普通の言い方で言えば、支出側と収益側のすべてのキャッシュフローの現在価値を合算したものと言った方が分かりやすいかもしれません。

プライバシーポリシー お問い合わせ