証券投資(現代ポートフォリオ理論)をコンパクトに学ぶべく、比較的最近に発刊され薄めの本である
を参考に学んでいく。
- 前回:
3. ポートフォリオ理論
3.7. 無リスク資産を含むポートフォリオ
無リスク証券が存在するとして、無リスク資産を組み入れたポートフォリオを考える。このときには平均=分散モデル
における2つ目の制約条件は除去することになる。
無リスク証券および種類のリスク証券
を組入れ候補としてポートフォリオを組成するため、2つ目の制約条件の代わりに
が加わる。
無リスク証券のリターンをとし、各リスク証券の期待リターンを
とする。このときポートフォリオ
(ウェイト
)のリターン
は
で与えられる。ポートフォリオ・リターンの期待リターンおよび分散はそれぞれ
である。以上を踏まえ、無リスク証券を含めた平均=分散モデルは
で与えられる。
このモデルを解くことにする。Lagrangeの未定乗数を導入すれば
を得、これを偏微分することで
を得る。
この連立方程式をに関して解いていく。解を
として、1つ目の方程式から
を得、これを2つ目の式に代入することで
とまずが求まる。これを代入することで最適ポートフォリオ
が得られた。
またこれを代入することでポートフォリオの分散は
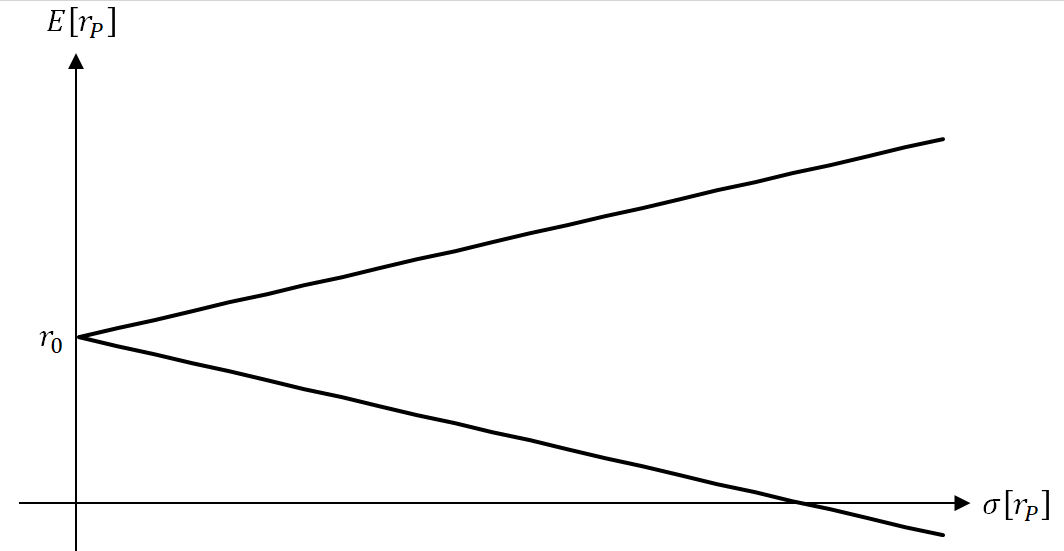
である。すなわち平面では放物線を描き、
平面では
軸上の切片を
とした傾き
の半直線を描く。
- 次回: