長期投資の理論と実践（07/X） - 「大人の教養・知識・気付き」を伸ばすブログ

　投資理論を以下の書籍

長期投資の理論と実践: パーソナル・ファイナンスと資産運用

作者:安達智彦,池田昌幸
東京大学出版会

Amazon

をベースに学ぶこととする。

前回

power-of-awareness.com

前回
4.　平均・分散分析とCAPM
- 4.3　市場均衡とCAPM
5.　CAPMの実証とJensenのalpha
- 5.1　CAPMとJensenの評価尺度
  - 5.1.1　Jensenのalpha
今回のまとめ
次回

4.　平均・分散分析とCAPM

　効用関数とリターンの従う確率分布に制約を加えるならば、期待効用を高めるポートフォリオはリターンの期待値と分散のみによって決定できる。

4.3　市場均衡とCAPM

　金融資産市場が完全競争的で無リスク資産への投資が可能ならば、平均・分散選好を持つ投資家は、無リスク資産と接点ポートフォリオへ最適な比率で投資すれば期待効用を最大化できる。無リスク資産と接点ポートフォリオへの投資資金の配分は、無差別曲線(リスク回避度)には依存するものの、接点ポートフォリオ自体の投資ウェイトベクトルはすべての投資家で同一である。そのため個別のリスク資産に対する総需要を考えると、各資産がリスク資産全体に占める割合はその資産が接点ポートフォリオに占める割合に一致する。
　ではリスク資産の供給をどう考えるか。1期間モデルにおいて、その供給は期初時点で所与と仮定するのが最も簡単な考え方である。リスク資産として株式を考えると、期初での各株式の総供給は時価総額に等しい。ある1つの株式銘柄について、縦軸に期初の株価、横軸に受容および供給量を考えると、株式の総供給が所与ならば、総供給直線は垂直に、総需要曲線は右下がりに描かれる。

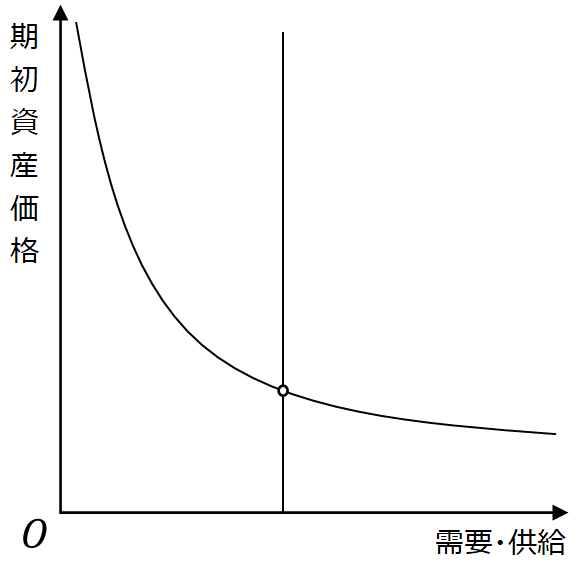両者の交点において均衡し、この均衡を市場均衡と呼ぶ。これを全資産に拡張すれば、各株式の価格が丁度妥当な期待リターンに対応するように株価が決定される。その均衡点では各投資家が受容する接点ポートフォリオに含まれる各株式価値の総合計は、各企業の発行済株式数で求めた株式時価総額の総合計に一致する。このとき接点ポートフォリオの構成は各企業の株式時価総額の比率で市場に存在するすべての株式を組み込んだものになっており、これこそが接点ポートフォリオを市場ポートフォリオと呼ぶ所以である。接点ポートフォリオは最小分散ポートフォリオであるため、市場ポートフォリオは必ず効率的フロンティア上に存在する。
　以上のように、主体的均衡と市場均衡が同時に達成されるとき、接点ポートフォリオは市場ポートフォリオになるため、

$\begin{aligned} &\mu_i-r_f=\beta_i(\mu_M-r_f),\\ \Leftrightarrow&E[\tilde{r}_i]=r_f+\beta_i(E[\tilde{r}_M]-r_f),\\ &\beta_i=\displaystyle{\frac{\mathrm{Cov}[\tilde{r}_i,\tilde{r}_M]}{V[\tilde{r}_M]}} \end{aligned}$

が成り立つ。これこそが $\mathrm{Fama}$ (1968)が導入した $\mathrm{CAPM}$ である。

5.　CAPMの実証とJensenのalpha

　 $\mathrm{CAPM}$ が現実に成立するかの実証分析にはベータと $\mathrm{Jensen}$ の $\mathrm{alpha}$ を活用して行う。

5.1　CAPMとJensenの評価尺度

　無リスク資産に投資可能な場合の $\mathrm{CAPM}$ の評価式

$\begin{aligned} E[\tilde{r}_i]&=r_f+\beta_i(E[\tilde{r}_M]-r_f),\\ \beta_i&=\displaystyle{\frac{\mathrm{Cov}[\tilde{r}_i,\tilde{r}_M]}{V[\tilde{r}_M]}} \end{aligned}$

を考える。
　実証分析上は、市場ポートフォリオが観測できないため、 $\mathrm{TOPIX}$ などのインデックスを代理変数として扱う。インデックスのリターンを $\tilde{r}_I$ とすれば、

$\begin{aligned} \tilde{r}_i-r_f&=\alpha_i+\beta_i(\tilde{r}_I-r_f)+\tilde{\varepsilon}_i,\\ E[\tilde{\varepsilon}_i]&=0,\\ \mathrm{Cov}[\tilde{\varepsilon}_i,\tilde{r}_I]&=0 \end{aligned}$

を評価式とする。
　標準的な $\mathrm{CAPM}$ の検証では、 $Y_t=\tilde{r}_i-r_f$ を目的変数、 $X_I=\tilde{r}_I-r_f$ を説明変数、そして $\tilde{\varepsilon}_i$ を誤差項として時系列データに対する回帰分析でベータを推定する。このような方法で推定したベータをヒストリカル・ベータという。
　この式の期待値を取ると、

$\begin{aligned} E[\tilde{r}_i]-r_f=\alpha_i+\beta_i(E[\tilde{r}_I]-r_f) \end{aligned}$

が得られ、仮に $\mathrm{CAPM}$ が成立し、また市場ポートフォリオの代理変数が市場ポートフォリオを十分に近似できているならば、 $\alpha_i\approx0$ でなければならない。またこれの線形和でもあるポートフォリオのアルファについても近似的に $0$ でなければならない。

5.1.1　Jensenのalpha

　 $\mathrm{Jensen}$ (1968)はもし資産運用上の技量において市場を凌駕する投資家が存在するならば、その投資家が運用するポートフォリオのアルファは正であるはずである。これが $\mathrm{Jensen}$ の $\mathrm{alpha}$ と呼ばれるものである。すなわち任意のポートフォリオ $p$ について

$\begin{aligned} \alpha_p&=(E[\tilde{r}_p]-r_f)-\beta_p(E[\tilde{r}_I]-r_f),\\ &=(\mu_p-r_f)-\beta_p(\mu_I-r_f) \end{aligned}$

と定義される。
　注意すべきは、もし金融資産市場が完全競争的で同質的期待形成が成立し、市場ポートフォリオが観測可能でしかも $\mathrm{CAPM}$ が成立するならば、正のアルファも負のアルファも取り得ない。推定された $\mathrm{Jensen}$ の $\mathrm{alpha}$ が有意に $0$ でなければ、市場が効率的でない、 $\mathrm{CAPM}$ 、もしくは市場インデックスが市場ポートフォリオの代理変数として不適切だったと考えられる。

今回のまとめ

金融資産市場が完全競争的で無リスク資産への投資が可能ならば、平均・分散選好を持つ投資家は、無リスク資産と接点ポートフォリオへ最適な比率で投資すれば期待効用を最大化できる。無リスク資産と接点ポートフォリオへの投資資金の配分は、接点ポートフォリオ事態の投資ウェイトベクトルはすべての投資家で同一で、そのため各資産がリスク資産全体に占める割合はその資産が接点ポートフォリオに占める割合に一致する。

このときリスク資産の需給について供給は期初時点で所与と仮定すると、期初での各株式の総供給は時価総額に等しい。両者の交点において均衡し、この均衡を市場均衡と呼ぶ。均衡点では各投資家が受容する接点ポートフォリオに含まれる各株式価値の総合計は、各企業の発行済株式数で求めた株式時価総額の総合計に一致する。このとき接点ポートフォリオの構成は各企業の株式時価総額の比率で市場に存在するすべての株式を組み込んだものになっており、これこそが接点ポートフォリオを市場ポートフォリオと呼ぶ所以である。

$\mathrm{CAPM}$ が現実に成立するかの実証分析にはベータと $\mathrm{Jensen}$ の $\mathrm{alpha}$ を活用して行う。

実証分析上は、市場ポートフォリオが観測できないため、 $\mathrm{TOPIX}$ などのインデックスを代理変数として扱う。インデックスのリターンを $\tilde{r}_I$ とすれば、
$\begin{aligned}\tilde{r}_i-r_f&=\alpha_i+\beta_i(\tilde{r}_I-r_f)+\tilde{\varepsilon}_i,\\E[\tilde{\varepsilon}_i]&=0,\\\mathrm{Cov}[\tilde{\varepsilon}_i,\tilde{r}_I]&=0\end{aligned}$
を評価式とする。

任意のポートフォリオ $p$ について
$\begin{aligned}\alpha_p&=(E[\tilde{r}_p]-r_f)-\beta_p(E[\tilde{r}_I]-r_f),\\&=(\mu_p-r_f)-\beta_p(\mu_I-r_f)\end{aligned}$
を $\mathrm{Jensen}$ の $\mathrm{alpha}$ と呼ぶ。

推定された $\mathrm{Jensen}$ の $\mathrm{alpha}$ が有意に $0$ でなければ、市場が効率的でない、 $\mathrm{CAPM}$ 、もしくは市場インデックスが市場ポートフォリオの代理変数として不適切だったと考えられる。