中長期における資産運用の考え方を学ぶべく、
を整理していく*1。
目次
4. 政策アセット・ミックス
年金運用においてパフォーマンスの大部分を決める政策アセット・ミックスの構築方法を扱う。
4.1 平均-分散アプローチによる政策アセット・ミックス
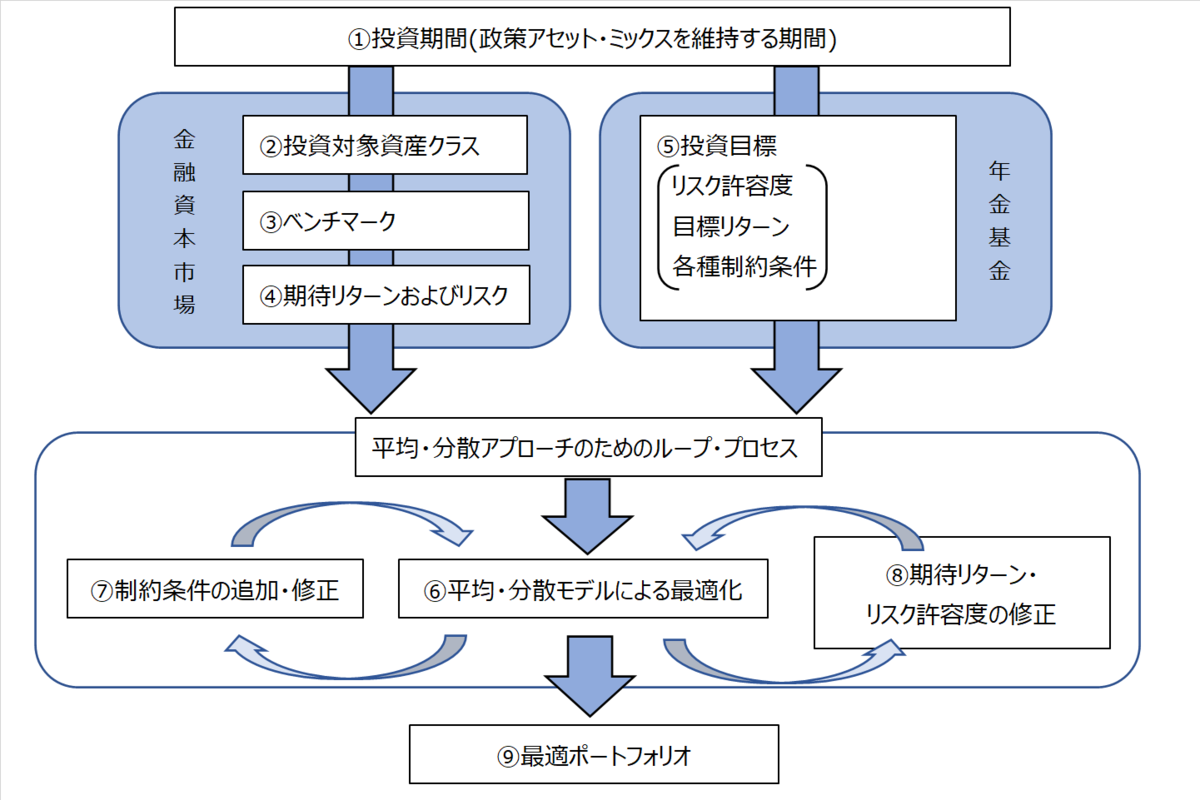
年金負債を明示的に考慮しないためアセット・オンリー・アプローチとも呼ばれる。年金基金に固有の投資目標や制約条件を考慮して、リスク・リターンの関係から見て効率的なアセット・ミックスを構築できる。
| (1) | 投資期間の決定 | |
| (2) | 投資対象資産クラスの選択 | |
| (3) | ベンチマークの設定 | |
| (4) | 期待リターン・リスク水準の設定 | |
| (5) | 投資目標の決定 | |
| (6) | 平均-分散モデルによる最適化 | |
| (7) | 制約条件の追加・修正 | |
| (8) | 期待リターンおよびリスク許容度等の調整 | |
| (9) | 最適ポートフォリオの決定 |
4.2 投資期間
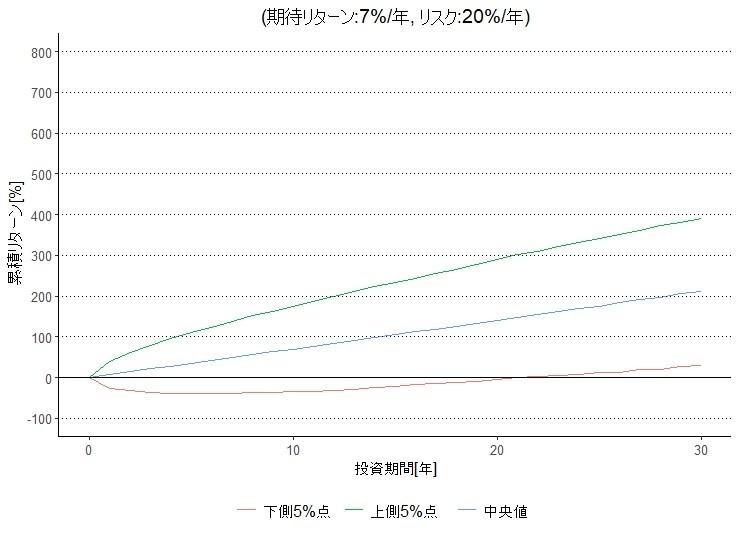
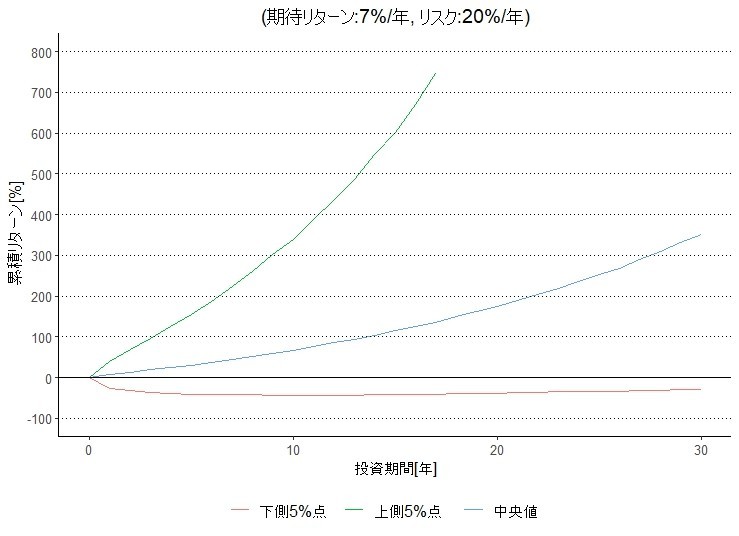
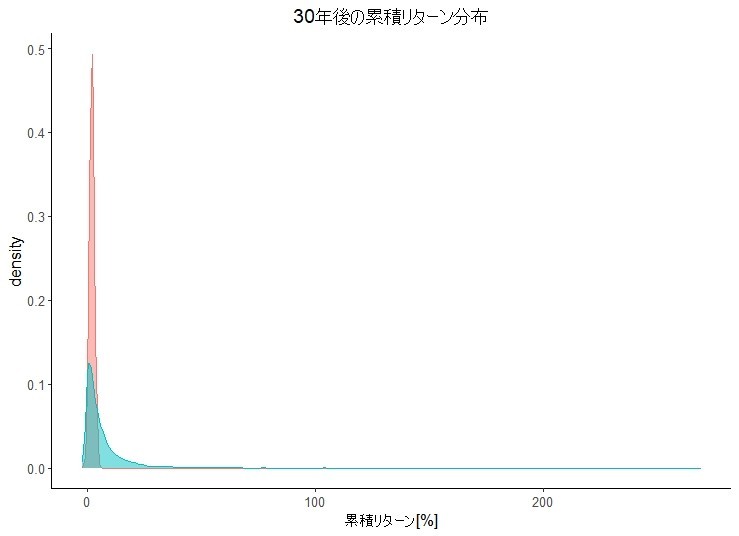
年金資産であれば投資期間は超長期と考えられる。これで問題になるのは、長期投資の累積リターンは複利(累積)になるために正規分布には従うとは限らないことである。
他方で、積立不足が発生する確率をリスクとして捉える年金運用では「時間分散効果を享受できるので、株式等のリスク性資産の投資ウェイトを高めるべき」と言われることがある。確かにショートフォール確率は時間が延びれば高くなる。しかし上述のシミュレーションからも明らかであるし、何より運動の性質からも明らかなように時間が延びれば延びるほどリスクは高くなる。したがって投資期間が長くても、現実には短期に実現した投資成果を新しい前提条件として、運用政策、積立政策および給付政策の各々の中で取り得る選択肢を逐次考慮し総合的に意思決定していくべきである。
4.3 投資対象資産クラスとベンチマーク
4.3.1 株式リターンの生成構造
年金運用では、可能な限り幅広くかつ複数の資産クラスに分散投資し、収益を獲得する機会を可能な限り捉えなければならない。基本となる投資対象資産クラスは
| (1) | 国内株式 | |
| (2) | 国内債券 | |
| (3) | 外国株式 | |
| (4) | 外国債券 |
があり、これらを総称して伝統的資産と呼ぶ。これら以外にはオルタナティブ資産(不動産、エマージング市場株式、ヘッジファンド、プライベート・エクイティなど)がある。
投資家(市場)が評価した資産価格(需要サイド)の過去データ自体を直接分析する方法は1つの有用性を持つ。他方で(株式)リターンを生み出す背景となる経済の生産構造(供給サイド)も併せて考えておくと理解がより一層深まる。
4.3.2 資産クラスの特性
資産クラスの切り分けと資産クラス内のスタイルでの切り分けのくぁけは悩ましい問題である。細分化の判断に明確な基準は存在せず、現実的な対応を取ることが必要になる。
良く行われるのは、各資産クラスを代表する市場インデックスをベンチマークとして採用し、そのベンチマークを検討する方法である。たとえば
| (1) | 国内株式 | 配当込み |
|
| (2) | 国内債券 | ||
| (3) | 外国株式 | グロス配当込み円ベース |
|
| (4) | 外国債券 | 円ベース |
が良く用いられる。ただしベンチマークとして用いられる市場インデックスには様々な問題点が指摘されており、カスタマイズド・インデックスの導入も含めた最適なベンチマーク設定が重要である。
4.4 期待リターンの予測
期待リターンの予測方法には代表的な手法が4つある:
| (1) | 過去平均法 | 過去のリターン実績値の算術平均を取る。 | |
| (2) | ビルディング・ブロック法 | 期待リターンを様々な構成要素に分解し、各要素の予測値をそれぞれ最適な方法で得、それらを合算する。 | |
| (3) | シナリオ法 | 様々な情報に基づき、予測者の判断で将来のリターンとその発生確率についてシナリオを作成し、その結果の期待値を取る。 | |
| (4) | インプライド・リターン法 | 他の市場参加者の保有ポートフォリオに内包された相場見通しを平均・分散モデルを用いて逆算する。 |
4.4.1 過去平均法
において
の過去実績リターンを用いて
とする。過去平均法は、
- 期待リターン・リスクは時間で常に一定
- リターンに系列相関が無い
ことを前提とする。
4.4.2 ビルディング・ブロック法
期待リターンがリスクフリーレートや種々のリスク・プレミアムから構成されると仮定し、各要素の予測値を合算して期待リターンを求める。
たとえば
といった形に分解する。
ビルディング・ブロック法は過去平均法よりも柔軟な予測が行える一方で、大きな構造変化が起こったと考えられる場合には対応しづらい。
4.4.3 シナリオ法
将来のマクロ経済状況について、悲観・中立・楽観などのいくつかのシナリオとそれぞれの発生確率を与える。各シナリオにおける資産のリターンを設定し、そのリターンの発生確率による加重平均を資産の期待リターンとする。
定性情報に基づく予測者の判断を重視するため、過去リターンの実績値が将来構造を反映しない状況だと考えられる場合には有効である。他方で客観性に欠ける。
4.4.4 インプライド・リターン法
他の市場参加者が平均・分散モデルを利用していると考え、その平均的なアセット・ミックスから平均・分散モデルを活用して逆算し、市場参加者が想定している期待リターンを求める方法である。
すなわち資産の期待リターン
を、資産
のリスク
、投資家のリスク回避度
、資産
への投資比率
および資産
と資産
のリターンの相関係数を
として
で与える。
インプライド・リターン法では、他の市場参加者が平均・分散モデルを用いること、計算で用いるリスク、相関係数
およびリスク回避度
が他の市場参加者と同じ値であることを前提とする。リスクおよび相関係数は過去のリターンの実績値から求め、リスク回避度
は仮置きする。
各資産の期待リターンはリスク回避度に依存して定まるが、リスク回避度
を客観的かつ合理的に推定することは不可能であるから、この方法では絶対水準ではなく相対水準を参照するのが望ましい。
4.5 リスクの予測
4.5.1 予測方法の全体像
リスクはリターンに比べて比較的構造が安定しているため、過去の実績リターンのみを用いて予測するのが一般的である。リタ0ンそのもの、もしくはビルディング・ブロック法によるリスク・プレミアム部分の過去実績値の標準偏差をリスクとする方法をナイーブ法と呼ぶ。
ナイーブ法は過去のリターン生成構造が一定で、それが将来も変化しないことを前提とする。この場合、極力長期のデータを用いて計算する方が望ましい。
遠い過去のデータよりも過去のデータに含まれる情報を重視すべく、リターンの時系列データにウェイトを持たせて加重平均を求める方法を指数加重法という。この方法は短期のリスク構造を予測したいときに使う方が望ましい。
4.5.3 指数加重法
過去のデータを指数加重して用いることで遠い過去のリターン程リスク算出に与える影響が小さくなるように計算を行う。
4.6 最適ポートフォリオの選択
合理的な投資家による最適ポートフォリオ選択に当たっては、期待リターンと分散(平均からの距離の二乗)を用いる。この背景には、「資産のリターンが正規分布に従う」または「合理的な投資家の期待効用がリターンの2次関数で近似できる」という前提がある。しかし後者は、年金基金の効用関数が2次関数で近似できない恐れがあることに留意しなければならない。たとえば、リスク許容度が低い飢饉にとって、年金基金が負債を下回らないような運用がもっとも重要であり、そのため、資産価値が負債を下回らせるようなリターンでは急激に効用が下がり、他方で負債を大きく上回らせるようなリターンではあまり効用を大きくしないと考えられる。このような状況を2次関数では上手く表すことができないのである。
とはいえ、実務上はそうした効用関数の特定が困難であるため、効率的フロンティアからポートフォリオを選択する方法は、恣意的にならざるを得ない。ただし単純に予定利率よりも高い期待リターンを持つポートフォリオを選択する方法は、期待効用を最大化するのに必ずしも合理的とは言えない。そこで、
①目標リターンを設定する方法 ②ショートフォール制約を掛ける方法の2通りが考えられる。4.6.1 目標リターンの付与
目標リターンを付与し、その制約下でリスクが最小となるポートフォリオを求める方法は、実務でよく使われている。このとき、目標リターンの設定値をどうするかが争点になる。
安直に考えれば、予定利率にすればよいと言える。しかし年金基金の場合、①資産配分(運用政策)、②積立(掛金)政策の2つの方法で年金運用の問題に対処できる。逆に言えば、将来の掛け金変動リスクを許容する度合いに応じて目標リターン自体も変化させ得るため、目標リターンを予定利率に設定することが合理的とは限らない。結局のところ、個々の年金基金のリスクに対する考え方次第で決める。
4.6.2 ショートフォール制約の付与
リスクを判断する指標には、標準偏差の他、下方リスクなどがある。下方リスクを表すのに、を考えるのが一案である。もし資産のリターンが正規分布に従うと仮定すれば、ポートフォリオ時価を
期待リターンおよび標準偏差をそれぞれ
とおくと、
で与えられる(パーセント表示するならば、で与えられる。)。このショートフォール制約を満たした領域を考える。

4.6.3 パラメータの推定誤差問題
平均・分散モデルによる最適化には様々な問題がある。その1つにパラメータの推定誤差がある。一般に、期待リターンを過大評価したり、リスクを過小評価したりとパラメータの推定誤差は大きな問題である。
これに対する対策には、
*1:どうも最近の書籍でこれくらいしっかりと書いてある本が見当たらなかったので…