マクロ経済学（11/17）閉鎖経済での短期の経済分析 - 「大人の教養・知識・気付き」を伸ばすブログ

マクロ経済学第2版

作者:二神孝一,堀敬一
有斐閣

Amazon

前回

power-of-awareness.com

前回
11.　閉鎖経済での短期の経済分析
問題*6
解答

11.　閉鎖経済での短期の経済分析

11.1　短期のマクロ経済モデルの特徴

　ここでは、短期での景気循環を問題とする。

11.1.1　短期と長期の違い

　長期と比べたときの短期の特徴は、

期待と現実が平均的に一致しない場合がある
市場の価格調整メカニズムが機能しない場合がある

である。
　ここからの議論では、「経済環境が変化しても、将来のさまざまな経済変数が現時点の各変数の値から変化しない」と家計や企業が予想していると仮定する*1。このような仮定をおくと、家計は消費も貯蓄も変化させないで、あたかも翌期の所得が一定化のように行動することになる。
　また2番目の仮定は、価格が需給を一致させるように調整されるとは限らないことを述べている。

11.1.2　ここでのマクロ経済モデル

　前節での2つの仮定を踏まえ、

家計の現在の消費は現在の可処分所得に依存して決定される、
資本ストックは一定である

と設定する。これは、短期では将来所得の変化が現在の消費に影響しないことから、現在の可処分所得のみが現在の消費を決定する。
　また、将来の生産能力上昇を考慮した行動を家計や企業がしないため、資本ストックが一定だと仮定する。この仮定は更に、生産量の変化が雇用労働力の変化によりもたらされることを意味する。
　以降、2つの市場の均衡条件から $\mathrm{GDP}$ と利子率が決まる仕組みを考察する。

11.2　45度線分析

　閉鎖経済における財市場の総需要 $Y^D$ は、消費 $C$ 、設備投資 $I$ および政府支出 $G$ により定まる。すなわち、

$\begin{aligned} Y^D=C(Y-T)+I(r)+G \end{aligned}$

と表される*2。
　財の総供給を $Y^S$ とすれば、 $Y^S$ と国内総生産( $\mathrm{GDP}$ )と国内総所得( $\mathrm{GDI}$ )とが一致することから、

$\begin{aligned} \begin{eqnarray} \left\{ \begin{array}{l} Y^D=C(Y-T)+I(r)+G,\\ Y^S=Y \end{array} \right. \end{eqnarray} \end{aligned}$

を得る。均衡状態では $Y^D\equiv Y^S$ であるから、

$\begin{aligned} Y=C(Y-T)+I(r)+G \end{aligned}$

を得る*3。
　この分析では、 $r,G,T$ を外生変数(モデル外で定める変数)とし、 $Y$ を内生変数とする。簡単のため、家計がケインズ型消費関数、すなわち

$\begin{aligned} C=A+cY \end{aligned}$

で表されるものとする( $A$ は基礎消費、 $c$ は限界消費性向、 $Y$ は(可処分)所得だとする。)。すると、

$\begin{aligned} Y=A+c(Y-T)+I(r)+G \end{aligned}$

が成り立つ。したがってこのときのGDPを $Y^{*}$ とすれば、

$\begin{aligned} Y^{*}=\displaystyle{\frac{A-cT+I+G}{1-c}} \end{aligned}$

を得る*4。

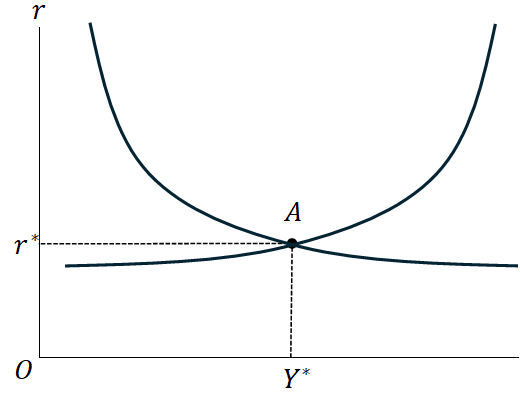
11.3　IS-LM曲線

11.3.1　財市場とIS曲線

　前章での「 $r,G,T$ を外生変数(モデル外で定める変数)とし、 $Y$ を内生変数とする」との仮説を緩やかにする、すなわち実質利子率 $r$ も内生変数だと仮定する。すると、均衡状態では

$\begin{aligned} Y^{*}=\displaystyle{\frac{A-cT+I(r)+G}{1-c}} \end{aligned}$

である。ここで実質利子率 $r$ の変化がGDPに与える影響を考えると、

$\begin{aligned} \displaystyle{\frac{dY}{dr}}&=\displaystyle{\frac{1}{1-c}}\displaystyle{\frac{dI}{dr}} \end{aligned}$

を得る。これは、 $\displaystyle{\frac{1}{1-c}}\gt0$ かつ $\displaystyle{\frac{dI}{dr}}\lt0$ *5であるから負である。
　ここから、均衡した財市場では金利の変化に対して単調に減少する。このような財市場を均衡させるような実質利子率とGDPの組の軌跡 $(r,Y)$ を $\mathrm{IS}$ 曲線という。

11.3.2　貨幣市場とLM曲線

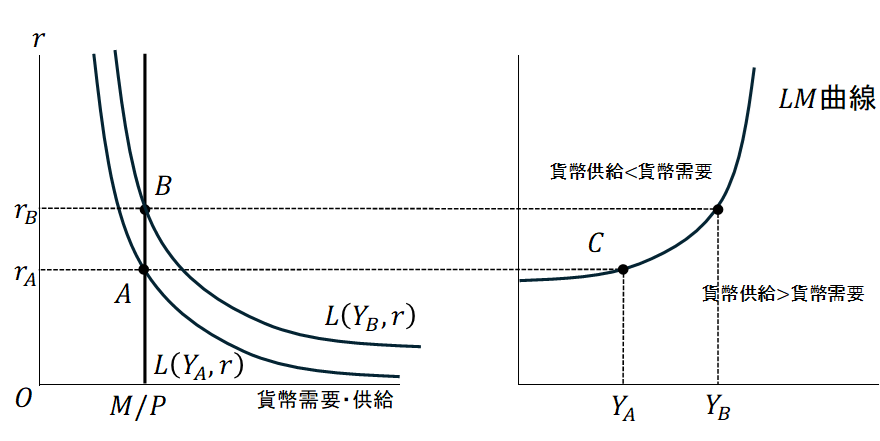
　次に貨幣市場を考える。ここでは物価水準 $P$ が外生変数で一定値を取るものと仮定する。また、名目貨幣量は中央銀行の政策で定まることから、ここでは所与で一定だとする。他方で、 $r,Y$ は内生変数だとする。すると、物価水準を一定だと仮定したことから、インフレ率は $0$ で名目利子率と実質利子率は一致する。したがって、貨幣市場での均衡条件は、実質貨幣需要関数を $L(Y,i)$ とすれば( $i$ は名目利子率)、

$\begin{aligned} \displaystyle{\frac{M}{P}}=L(Y,r) \end{aligned}$

で与えられる。ここで $L(Y,r)$ は $r$ の減少関数であるから、所与の $\mathrm{GDP}$ を $Y_A$ とすれば、実質貨幣需要関数 $L(Y_A,r)$ は $r$ の増加関数である。一方で、実質貨幣量は $r$ に依存しないから、縦軸に平行である。
　 $\mathrm{GDP}$ の水準が変化すると、貨幣市場の均衡はどのように変化するか。仮に $\mathrm{GDP}$ が $Y_A$ から $Y_B$ ( $Y_A\lt Y_B$ )に変化したと仮定する。 $L(Y,r)$ は $Y$ の増加関数であるから、 $r$ が一定ならば

$\begin{aligned} L(Y_A,r)\lt L(Y_B,r) \end{aligned}$

が成り立つ。したがって、 $\mathrm{GDP}$ の変化で実質貨幣需要関数はより右上に位置する。このように貨幣市場を均衡させると、 $(Y,r)$ の軌跡は右上がりである。この軌跡を $\mathrm{LM}$ 曲線という。

11.3.3　財市場と貨幣市場の均衡

　IS-LM分析を整理すると、外生変数を $G,T,M,P$ 、内生変数を $Y,$ $r$ とする。 $\mathrm{IS}$ 曲線は財市場を均衡させるような $(Y,r)$ で、 $\mathrm{LM}$ 曲線は貨幣市場を均衡させるような $(Y,r)$ である。したがって、財市場と貨幣市場を同時に均衡させるようなGDPと実質利子率は両曲線の交点である。

11.4　総需要・総供給分析

14.4.1　問題の設定

　物価水準、実質利子率および $\mathrm{GDP}$ を内生変数と考え、財市場、貨幣市場および労働市場を分析対象に加える。また家計や企業の将来に対する期待は、ある程度固定されており速やかには修正されないと仮定する。
　この下で、

$\mathrm{AD}$ 曲線：財市場と貨幣市場を同時に均衡させる $\mathrm{GDP}$ 、利子率 $r$ および物価水準 $P$
$\mathrm{AS}$ 曲線：労働市場で均衡した $\mathrm{GDP}$ および物価水準 $P$

を考える。

14.4.2　総需要曲線

　ある $\mathrm{GDP}$ 水準 $\bar{Y}$ を所与として貨幣需要関数 $L\left(\bar{Y},r\right)$ を考える。もし $P$ が上昇すれば $M/P$ が下落するため貨幣市場で均衡を保つために利子率 $r$ は上昇しなければならない。そのため $\mathrm{LM}$ 曲線は上方にシフトする。これにより $\mathrm{IS}$ 曲線と $\mathrm{LM}$ 曲線の交点は $\mathrm{GDP}$ は下落する方向に移動する。この変化は $P$ の上昇によりもたらされたのであり、したがって $P$ を縦軸、 $Y$ を横軸とすれば総需要曲線は単調減少である。

14.4.3　総供給曲線

　短期のマクロ経済モデルでは資本ストックは一定だと仮定している。そのため生産量の変化は、労働投入量の変化によりもたらされる。短期のマクロ経済モデルにおける総供給曲線は物価水準と生産量との関係を表す。では、なぜ部化k水準変化が労働投入量変化を通じて生産量を変化させるのか。

　説明する理論の1つには名目賃金率の下方硬直性がある。名目賃金に下方硬直性があるならば、失業は速やかに解消されず、財やサービス供給に影響を与える。労働需要および労働供給は実質賃金率 $W/P$ に依存するため、

$\begin{aligned} L^D&=L^D\left(W/P\right),\\ L^S&=L^S\left(W/P\right) \end{aligned}$

と表される。
　いま名目賃金率が $\bar{W}$ 、物価水準が $P^{\prime}$ であると仮定する。このときに企業に雇用される労働力は $L^{\prime}$ で、失業が発生している。しかし労働市場が競争的であれば名目賃金率が低下して均衡点にて労働の需給が一致し失業は解消する。
　しかし、失業者が存在していても名目賃金率は $\bar{W}$ から直ちに低下しない可能性がある。そこでもし物価水準が $P'$ から $P^{*}$ に上昇すれば、実質賃金率は $\bar{W}/P^{\prime}$ から $\bar{W}/P^{*}$ へ下落する。その結果、雇用労働者数は $L^{\prime}$ から $L^{*}$ へ増加して生産量も増加する。
　物価が $P^{*}$ 以上の水準に上昇した場合、どうなるか。このとき労働供給が労働需要を下回っている。そのため、企業は名目賃金率を $\bar{W}$ よりも高めようとするはずで、労働市場が均衡するまで上昇する。すなわち実質賃金率が $\bar{W}/P^{*}$ に等しくなるまで名目賃金率は上昇するが、そのときの雇用労働量は $L^{*}$ のままでは変化しない。したがって経済で生産される財・サービスの水準も変化しない。

　説明する理論のもう1つには予想誤差モデルがある。物価水準 $P$ が変化しても、家計はその変化を直ちには把握できない一方で、企業は直ちに把握できると仮定する。この場合、家計は自身が予想する期待物価水準 $E[P]$ に基づき労働供給を決定する。
　このような仮定の下で労働市場の均衡が達成される。名目賃金率 $W$ および労働量 $L$ に対して、労働供給関数 $L^S=L^S(W/S)$ 、労働需要関数 $L^D=L^D(W/S)$ である。 $P$ が変化すると、 $W/P$ も変化するから、これにより労働需要も労働供給も変動する。そのため $W$ が一定であっても $P$ の水準に応じて複数の労働需要・供給曲線が存在する。もし現時点での物価水準が $P^*$ で家計もそれを認識しているのであれば、労働市場は均衡する（均衡点を $A$ とし、そこでの各水準を $(L^{*},W_A)$ とする。）。
　何らかの理由で物価水準が $P^{*}$ から $P^{\prime}$ へ上昇したと仮定する。すると仮定より、家計の認識する物価水準は $E[P]=P^{*}$ のままで労働供給関数が変化しない一方で、企業は実質賃金率が低下すると理解しているため、労働需要を増やす。その結果、労働需要関数は $L^{D}(W/P^{*})$ から $L^{D}(W/P^{\prime})$ に変化（右側へシフト）する。これにより、新たな均衡点 $B$ に至る。ここでは点 $A$ に比べて名目賃金率が $W_B$ に上昇するものの、家計の期待物価水準は $P^{*}$ のままであるから、実質賃金率が上昇したと錯覚し、労働供給を増加させる。これにより雇用労働量は $L^{*}$ から $L^{\prime}$ へ増加し、企業の生産量も増加する。
　ところが、一定期間が経過すると、家計は自分の認識する物価水準と実際の水準とに相違があることに気づく。そこで家計は $E[P]=P^{\prime}$ へと修正し、労働供給を減少させる。その結果、労働供給曲線は $L^S(W/P^{*})$ から $L^S(W/P^{\prime})$ へとシフトし、均衡点がさらに変化する。これにより、名目賃金率が $W_B$ から $W_C$ に上昇する一方で、雇用労働量は $L^{\prime}$ から $L^{*}$ へ減少する。

　このように、総供給曲線は3つ存在する。まず期待物価水準が現実の物価水準に等しい場合、名目賃金率の下方硬直性の有無で総供給曲線が変化する。このとき、物価水準 $P$ の変化に応じて名目賃金率は速やかに調整されるため、労働市場では常に需給が一致する。
　もし負の生産性ショックが発生し設備投資が減少した場合、総需要曲線は左にシフトし、物価水準及び $\mathrm{GDP}$ はともに下落する。物価水準が下落することで実質賃金率が上昇するため、家計は労働供給を増やす一方で企業は労働需要を減らす。これにより、失業が発生する。もし名目賃金率が速やかに下方に調整されれば失業は解消する一方で、下方硬直性があれば失業が発生し続ける。
失業の発生や $\mathrm{GDP}$ の低下は、しばらく経つと名目賃金率の低下をもたらす。これにより、総供給曲線の右上がりの部分が右にシフトする。
　物価水準が一定である中で名目賃金率が低下すれば、実質賃金率も低下する。これにより家計は労働供給を減少させる一方で、企業の労働需要は増加する。失業が発生しているイ間、企業の労働需要が雇用労働量を決定する。これにより当初の均衡点に対し、失業者数は減少し、雇用労働量は増加して $\mathrm{GDP}$ も増加する。
　最終的に完全雇用均衡が回復され、 $\mathrm{GDP}$ は特定の水準まで戻る。ただし、物価水準は当初よりも低下したままである。

11.5　景気循環と経済政策

11.5.1　経済政策の役割

　完全雇用均衡からの乖離によって発生する景気循環を、より速やかに安定化させるにはどのような政策が必要か。そのために、政府支出 $G,$ 租税 $T,$ 名目貨幣量 $M$ などの外生変数が変化した場合に、 $\mathrm{GDP}$ や物価水準、実質利子率などの内生変数にどのような影響を与えるかを考える。

11.5.2　財政政策

　まず45度線分析では、政府支出 $G$ の変化により均衡 $\mathrm{GDP}$ はどの程度変化するか。これは均衡 $\mathrm{GDP}$ を $G$ により偏微分すればよく、

$\begin{aligned} \displaystyle{\frac{\partial Y^{*}}{\partial G}}&=\displaystyle{\frac{\partial}{\partial G}}\left(\displaystyle{\frac{A-cT+I+G}{1-c}}\right),\\ &=\displaystyle{\frac{1}{1-c}} \end{aligned}$

である。これを政府支出乗数という。 $0\lt c\lt1$ であるから、政府支出乗数は $\gt1$ である、すなわち政府支出が増加すれば、それ以上に $\mathrm{GDP}$ が増加することを意味する。
　同様に、租税 $T$ の変更が均衡 $\mathrm{GDP}$ に与える影響についても考えると、

$\begin{aligned} \displaystyle{\frac{\partial Y^{*}}{\partial T}}&=\displaystyle{\frac{\partial}{\partial T}}\left(\displaystyle{\frac{A-cT+I+G}{1-c}}\right),\\ &=-\displaystyle{\frac{c}{1-c}} \end{aligned}$

である。租税乗数は負になるから、増税すれば $\mathrm{GDP}$ が下落するのに対して、減税すれば $\mathrm{GDP}$ が増大する。

　他方、政府支出が変化すると $IS$ 曲線にはどのような影響を与えるか。政府支出が $\Delta G$ だけ増加すると、 $\mathrm{GDP}$ は $\displaystyle{\frac{\Delta G}{1-c}}$ だけ増加する。この増加は実質利子率 $r^{*}$ の下で生じているが、 $r$ のいずれの水準であっても $\mathrm{GDP}$ は増加する。
　しかし、 $IS$ - $LM$ 分析では、均衡 $\mathrm{GDP}$ の増加幅が低下する。これは、実質利子率が上昇することで、設備投資が減少したからである。このように政府支出増加に伴い設備投資が減少する現象をクラウディング・アウトという。
　一方で、政府支出が増加すると、クラウディング・アウトの程度にかかわらず、政府支出の増加は結果的に $\mathrm{GDP}$ を増加させる。一方、物価水準 $P$ および $LM$ 曲線は一定のままである一方で、 $P$ の水準にかかわらず $\mathrm{GDP}$ は増加しており、政府支出の増加に伴い総需要曲線は右側へシフトする。

11.5.3　金融政策

　次に、金融政策が総需要曲線に及ぼす影響を考える。物価水準 $P$ を所与として、当初の名目貨幣量が $M$ だと仮定する。 $\mathrm{GDP}$ 水準が $\bar{Y}$ である場合、貨幣需要関数は $L\left(\bar{Y},r\right)$ である。このときの均衡点を $A$ 、実質利子率を $r_A$ とする。
　中央銀行が名目貨幣量を $M$ から $M^{\prime}$ へ増加させたと仮定する。すると実質貨幣量を表す直線は右にシフトする。その結果、 $\mathrm{GDP}$ 水準が $\bar{Y}$ のままでも均衡実質利子率は $r_A$ から $r_B$ へと低下する。この実質利子率の低下は、 $\bar{Y}$ 以外のいずれの水準であっても生じる。
　すると、 $IS$ - $LM$ 分析における均衡も移動する。すなわち名目貨幣量の増加で、財市場と貨幣市場を同時に均衡させる $\mathrm{GDP}$ は上昇し、実質利子率は下落している。さらにこのとき、総需要曲線は右側へシフトする。

11.5.4　総需要管理政策

　政府支出の増加、減税あるいは名目貨幣量の増加は、総需要曲線を右側へシフトさせる。このような総需要の変化に基づく政策を総需要管理政策という。
　総需要管理政策は、総供給に対する府のショックにも対応することも可能である。
　次に、原油価格の上昇など、企業の生産性に負のショックが発生した場合、総供給曲線を上方にシフトさせることになる。その結果、物価上昇と $\mathrm{GDP}$ 減少を同時にもたらす。これをスタグフレーションという。このとき、もし政府が総需要管理政策を実施して総需要曲線をシフトさせれば、物価水準が上昇する一方で完全雇用 $\mathrm{GDP}$ の回復を実現できる。

11.5.5　マクロ計量モデルとルーカス批判

　政府支出の増で経済を完全雇用 $\mathrm{GDP}$ にまで回復させるのであれば、政府は支出額を過不足ないように決定しなければならない。それには、総需要曲線や総供給曲線の形状を正しく理解しなければならない。しかし、それらは観測できるわけではないため、過去のデータから推計することになる。このように過去のデータから推計されたマクロ経済のモデルをマクロ計量モデルという。
　マクロ計量モデルは、経済を表現するいくつかの方程式から構成され、内生変数や外生変数などとの関係を表す構造パラメータを含む。
　しかし、 $\mathrm{Lucas}$ (1976)は、マクロ計量モデルに基づく総需要管理政策を批判した。その主旨は、マクロ計量モデルで推定されたパラメータの推定値は、経済政策の実行で変化するため、適切な総需要管理政策の決定は不可能だというものである。

問題*6

1.　45度線分析

　消費関数が $C=10+0.8(Y-T)$ で表されるとき、45度線分析を用いて以下の問いに応えよ。なお $C$ は消費、 $Y$ は $\mathrm{GDP}$ (国内総所得)、 $T$ は租税を表す。

(a) 政府支出が $20$ 、租税が $20$ 、設備投資が $30$ であることを仮定する。このときの均衡 $\mathrm{GDP}$ を求めよ。
(b) 政府支出乗数、租税乗数を求めよ。
(c) 政府支出と租税が一致する均衡財政政策を政府が採用していることを仮定する。1兆円の政府支出の増加は $\mathrm{GDP}$ をいくら増加させるか計算せよ。

2.　IS-LM分析①

　消費関数 $C$ 、設備投資関数 $I$ 、貨幣需要関数 $L$ がそれぞれ

$\begin{aligned} C&=A+c(Y-T),\\ I&=\bar{I}-vr.\\ L&=\bar{L}+kY-lr \end{aligned}$

で表されるとして以下の問いに答えよ。ここで、 $Y$ は $\mathrm{GDP}$ 、 $r$ は実質利子率、 $T$ は租税を表し、 $A,c,\bar{I},v,$ $\bar{L},k,l$ はそれぞれ正の定数とする。

(a) 財市場の均衡条件を $Y=C+I+G$ とするとき、 $IS$ 曲線を求めよ。ただし $G$ は政府支出を表す。また名目貨幣量を $M,$ 物価水準を $P$ で表すとして $LM$ 曲線を求めよ。
(b) 均衡における $\mathrm{GDP}$ と実質利子率を求めよ。

3.　IS-LM分析②

　以下の方程式で表されるような経済を考えるとき、以下の問いに答えよ。

$\begin{aligned} C&=500+0.8(Y-T),\\ I&=4500-500r,\\ L&=500+2Y-1000r \end{aligned}$

ここで $Y$ は $\mathrm{GDP}$ 、 $r$ は実質利子率、 $T$ は租税、 $C$ は消費、 $I$ は設備投資、 $L$ は貨幣需要を表す。
　また財市場の均衡条件は $Y=C+I+G$ で、政府支出は $G=3000$ だと仮定する。さらに実質貨幣量を $20500$ とする。

(a) 均衡財政政策の場合の $IS$ 曲線と $LM$ 曲線を求めよ。
(b) このとき均衡国民所得と均衡利子率を求めよ。
(c) 均衡財政政策を保ったまま政府支出が $G=6000$ に増加した。このときの均衡国民所得と均衡利子率を求めよ。

4.　労働と総需要

　企業は労働のみを用いて生産を行い、企業の生産関数が $Y=\sqrt{L}$ であると仮定する。ここで $Y$ は企業の財の生産量、 $L$ は労働投入量を表す。また名目賃金率 $\bar{w}$ は硬直的で、財の価格を $p$ で表すこととする。

(a) 企業の労働需要関数を求めよ。
(b) 総供給関数を求めよ。
(c) この経済の総需要関数を $Y=p^{-1}$ だと仮定する。このときの均衡財価格と均衡生産量を求めよ。

5.　企業と家計

　経済に代表的企業と代表的家計が1つずつ存在するとし、生産および取引される財は1種類のみだと仮定する。また家計の効用関数は、

$\begin{aligned} u=c+l-\displaystyle{\frac{1}{2}}l^2 \end{aligned}$

と書けるものとする。ここで $c$ は財の消費量、 $l$ は余暇に費やす時間を表している。なお家計の労働時間の上限を $1$ とする。名目賃金率を $w,$ 財の価格を $p$ で表す。家計の所得は労働所得のみであることも仮定する。企業は労働のみを用いて生産を行い、企業の生産関数を $Y=L-\displaystyle{\frac{1}{2}}L^2$ とする。 $Y$ は企業の財の生産量、 $L$ は労働投入量を表している。

(a) 家計が財の価格を $p^e$ と予想しているとき、家計の労働供給関数を求めよ。
(b) 企業は財の価格を正確に知っていると仮定する。このとき企業の労働需要関数を求めよ。
(c) 労働市場を均衡させる名目賃金率を求めよ。
(d) 家計の予想価格 $p^e$ を所与として、生産量を $p$ の関数で表すことにより、総供給関数を導出せよ。