マクロ経済学（10/17）労働市場 - 「大人の教養・知識・気付き」を伸ばすブログ

　基本的な経済観念を身に付けるべく、マクロ経済学を学んでいく。テキストは古典派をしっかりと扱っているという

マクロ経済学第2版

作者:二神孝一,堀敬一
有斐閣

Amazon

を用いることにする。

前回

power-of-awareness.com

前回
10. 　労働市場
次回
問題*3
解答

10. 　労働市場

10.1　失業の定義と分類

10.1.1　失業の定義と分類

　失業率は労働力人口に占める失業者数の比率である。労働力人口は、日本においては15歳以上の人口を

　　①就業者

　　②完全失業者

　　③非労働力

に分類したうえで、①と②の和を取った数として定義される。他方で国際労働機関( $\mathrm{ILO}$ )は、完全失業者を

　(a) 仕事を持たない

　(b) 仕事を探している

　(c)直ぐに仕事に就ける

人物として定義している。

10.1.2　なぜ失業者が存在するのか

　企業は労働力を需要し、家計は労働力を供給する。需給が一致するように賃金が調整されれば失業者はいなくなるはずである。しかし労働市場で賃金が直ちに調整されるとは限らず、労働契約における法的規制や慣習、解雇のルールなど労働に関する摩擦は非常に多い。このような事情により失業者が発生すると考えられている。

10.2　労働市場の均衡

10.2.1　労働供給

　労働の供給主体は家計である。簡単のために異時点間の消費や余暇の選択を無視すれば、家計はある1時点の効用最大化問題を解くことで労働供給を決定する。 $t$ 期の余暇を $H_t$ とし $t$ 期の労働時間を $L_t$ とする。労働ないし余暇の時間上限を $\bar{L}$ とすれば、 $H_t+L_t=\bar{L}$ である。財の消費だけでなく余暇の時間を過ごすことでも効用を得ると考えれば、この家計の効用は

$\begin{aligned} U\left(C_t,H_t\right)=u\left(C_t\right)+z\left(H_t\right) \end{aligned}$

で表すことができる。
　次に家計の予算制約式を考える。家計が労働所得と資産からの所得で財を購入すると仮定すると、

$\begin{aligned} W_tL_t+A_t=P_tC_t \end{aligned}$

が成り立つ。ここで各変数は以下のとおりだとする。

$C_t$	$t$ 期の財の消費量
$W_t$	$t$ 期の名目賃金率
$A_t$	$t$ 期の資産所得
$P_t$	$t$ 期の消費財価格(物価水準)

　予算制約式に時間に対する制約式を代入することで

$\begin{aligned} P_tC_t=W_t\left(\bar{L}-H_t\right)+A_t \end{aligned}$

を得る。
　以上から、消費と余暇の選択に関する効用最大化条件は、以下のように展開できる。まず

$\begin{aligned} W_tL_t+A_t&=P_tC_t\\ W_t\left(\bar{L}-H_t\right)+A_t&=P_tC_t\\ W_t\bar{L}+A_t&=P_tC_t+W_tH_t \end{aligned}$

で、次に $I_t\equiv W_t\bar{L}+A_t$ と定義すると、

$\begin{aligned} P_tC_t&=I_t-W_tH_t\\ C_t&=\displaystyle{\frac{I_t-W_tH_t}{P_t}} \end{aligned}$

が導かれる。これを効用関数に代入することで

$\begin{aligned} U\left(C_t,H_t\right)&=u\left(C_t\right)+z\left(H_t\right)\\ &=u\left(\displaystyle{\frac{I_t-W_tH_t}{P_t}}\right)+z\left(H_t\right) \end{aligned}$

を得る。両辺を $H_t$ に関して偏微分して $0$ とおくと

$\begin{aligned} \displaystyle{\frac{\partial U\left(C_t,H_t\right)}{\partial H_t}}&=\displaystyle{\frac{\partial}{\partial H_t}}\left\{u\left(\displaystyle{\frac{I_t-W_tH_t}{P_t}}\right)+z\left(H_t\right)\right\}\\ &=\left(-\displaystyle{\frac{W_t}{P_t}}\right)u^{\prime}(C_t)+z^{\prime}(H_t)=0 \end{aligned}$

を得、これから

$\begin{aligned} \left(-\displaystyle{\frac{W_t}{P_t}}\right)u^{\prime}(C_t)+z^{\prime}(H_t)&=0\\ \displaystyle{\frac{z^{\prime}(H_t)}{u^{\prime}(C_t)}}&=\displaystyle{\frac{W_t}{P_t}} \end{aligned}$

を得る。これは余暇と消費財の限界効用の比率、すなわち限界代替率が実質賃金率に等しくなることを意味する。ただし $H_t+L_t=\bar{L}$ が成り立っているから、余暇の時間が決まれば自動的に労働供給の時間が決定される。

　効用最大化の条件から労働供給が如何に決まるかを確認する。

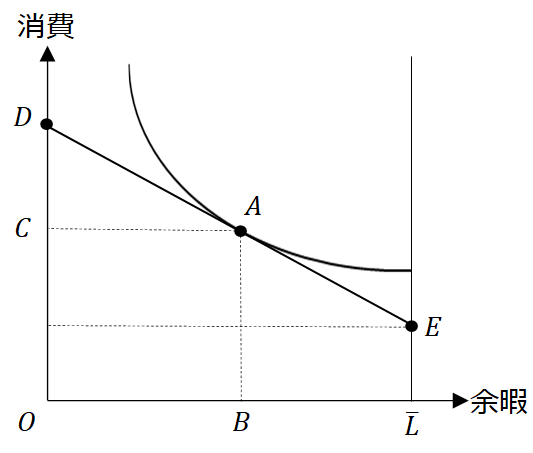
　消費者は上図の条件において、無差別曲線と予算制約線の接点である点 $A$ で財の消費量および余暇を決定する。すなわち $OC$ の長さ分だけ財を消費し、 $OB$ だけ余暇を過ごし、労働供給は $B\bar{L}$ になる。

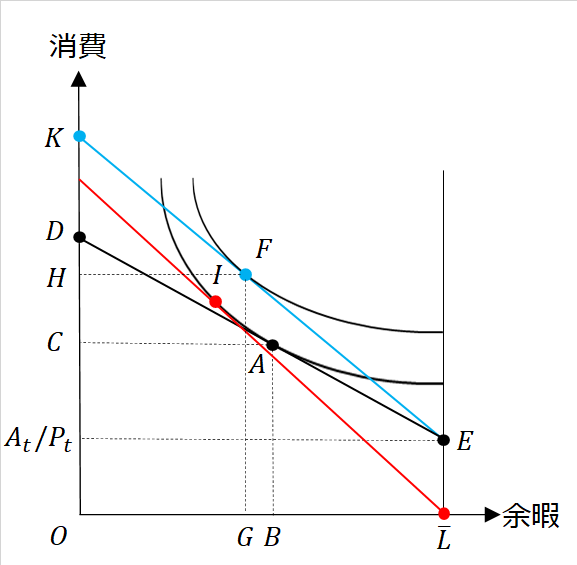
　次に賃金率が上昇した場合を考える。賃金率が上昇して実質賃金率が $W_t/P_t$ から $\left(W_t/P_t\right)^{\prime}$ に上昇したと仮定する。この場合、最適な消費財と余暇の組み合わせは点 $A$ から点 $F$ へと変化する。これにより $HC$ だけ財の消費が増え、 $GB$ 分だけ労働供給が増加(=余暇が減少)する。
　これは

代替効果：点 $A$ →点 $I$
所得効果：点 $I$ →点 $F$

という2つの効果を受けたものである。実質賃金率の上昇が労働供給の増加につながるか否かは代替効果と所得効果の相対的な強さに依存しており、

①	代替効果 $\gt$ 所得効果	→	労働供給の増加
②	代替効果 $=$ 所得効果	→	労働供給と余暇に変化なし
③	代替効果 $\lt$ 所得効果	→	労働供給の減少

このような変化を表したのが以下のような曲線で、これを労働供給曲線 $L_t=L^S\left(W_t/P_t\right)$ という。

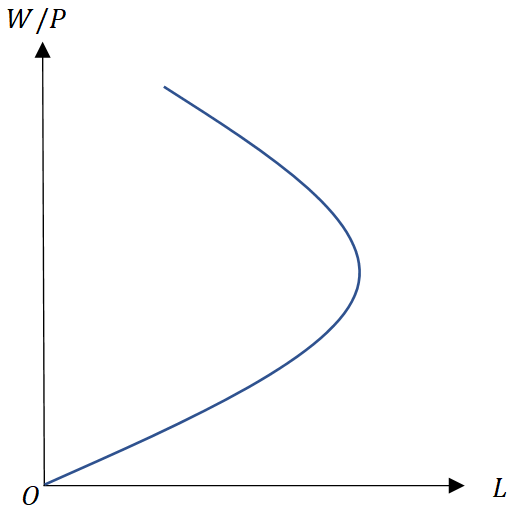
10.2.2　労働需要

　労働を需要する経済主体は企業である。企業の目的は利潤最大化であるから、労働需要は企業の利潤最大化問題の解として表される。企業の財生産量が労働のみに依存すると仮定する。利潤を $\Pi_t,$ 労働を $L_t$ とし、 $F(L_t)$ を生産関数(更に $F^{\prime}\left(L_t\right)\gt0,$ $F^{\prime\prime}\left(L_t\right)\lt0$ と仮定する。)、 $P_t$ を生産物価格、 $W_t$ を名目賃金率とすれば、利潤関数は

$\begin{aligned} \Pi_t=P_t F\left(L_t\right)-W_tL_t \end{aligned}$

と表される。このとき $L_t$ に関する利潤最大化条件は

$\begin{aligned} &\displaystyle{\frac{\partial \Pi_t}{\partial L_t}}=\displaystyle{\frac{\partial}{\partial L_t}}\left(P_t F\left(L_t\right)-W_tL_t\right)=0\\ \Leftrightarrow&P_t\displaystyle{\frac{\partial F\left(L_t\right)}{\partial L_t}}-W_t=0\\ \Leftrightarrow&\displaystyle{\frac{\partial F\left(L_t\right)}{\partial L_t}}=\displaystyle{\frac{W_t}{P_t}} \end{aligned}$

となる。左辺は労働の限界生産性で右辺は実質賃金率で、これらが等しくなるような水準で労働需要が決まる。ここから、

実質賃金率の上昇(下落)　→　労働需要の減少(増加)

が導かれる。このことから、労働需要関数 $L_t=L^D\left(W_t/P_t\right)$ は実質賃金率の関数として表される。

10.2.3　均衡実質賃金と雇用量の決定

　前述した労働供給関数 $L_t=L^S\left(W_t/P_t\right)$ と労働需要関数 $L_t=L^D\left(W_t/P_t\right)$ との交点として均衡雇用量 $L^{*}$ および均衡実質賃金率 $\left(W_t/P_t\right)^{*}$ が決まる。

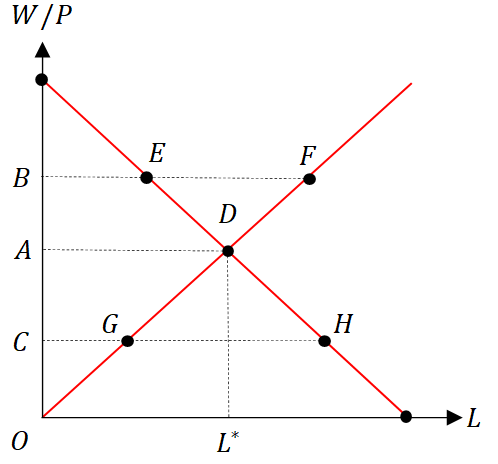
　仮に実質賃金率が $\left(W_t/P_t\right)^{*}$ を超過してたとえば点 $B$ の水準にある場合、労働需要は点 $E$ の水準( $L^{D}_{\mathrm{excess}}$ )、労働供給は点 $F$ の水準( $L^{S}_{\mathrm{excess}}$ )にあり、したがって超過供給 $L^{S}_{\mathrm{excess}}-L^{D}_{\mathrm{excess}}$ （すなわち労働供給が余っている状態）が生じることになる。このような状態を失業が発生しているという。もし労働市場の価格調整メカニズムが伸縮的（うまく調整が働く状態）であれば、名目賃金率が低下し失業が解消する水準にまで実質賃金率が低下する。
　逆に、実質賃金率が $\left(W_t/P_t\right)^{*}$ よりも低くたとえば点 $C$ の水準にある場合、労働需要は点 $G$ の水準( $L^{D}_{\mathrm{short}}$ )、労働供給は点 $H$ の水準( $L^{S}_{\mathrm{short}}$ )にあり、したがって超過需要 $L^{D}_{\mathrm{short}}-L^{S}_{\mathrm{short}}$ （すなわち労働供給が不足している状態）が生じることになる。このような場合には実質賃金率が均衡実質賃金率まで上昇し超過需要は解消されることになる。

10.3　失業の理論

　このような労働市場の均衡は、現実の失業を説明するのは難しい。
　現実の失業を説明するためには労働市場モデルを修正する必要がある。そのために実質賃金の下方硬直性が生じるモデルと労働者と企業の間でミスマッチが生じるモデルを導入する。

10.3.1　実質賃金の下方硬直性

　実質賃金が下方硬直性（価格がある水準に一度でも到達すると、その水準を下回ることが困難になる性質）を持つのであれば、労働の超過供給により失業が発生する。このような場合、失業者がより低い賃金で働くことを申し出たとしても失業者が雇用されることはない。では、なぜ賃金は労働市場が均衡する水準まで低下しないのか。それを説明する理論の1つがインサイダー・アウトサイダー理論である。

10.3.2　実質賃金の下方硬直性による失業

　インサイダー・アウトサイダー理論は、労働組合が現労働者や労働組合員の賃金引き上げの実を目的として失業者のために賃金の引き下げに応じないような交渉を使用者と行うことで失業が発生すると考える。

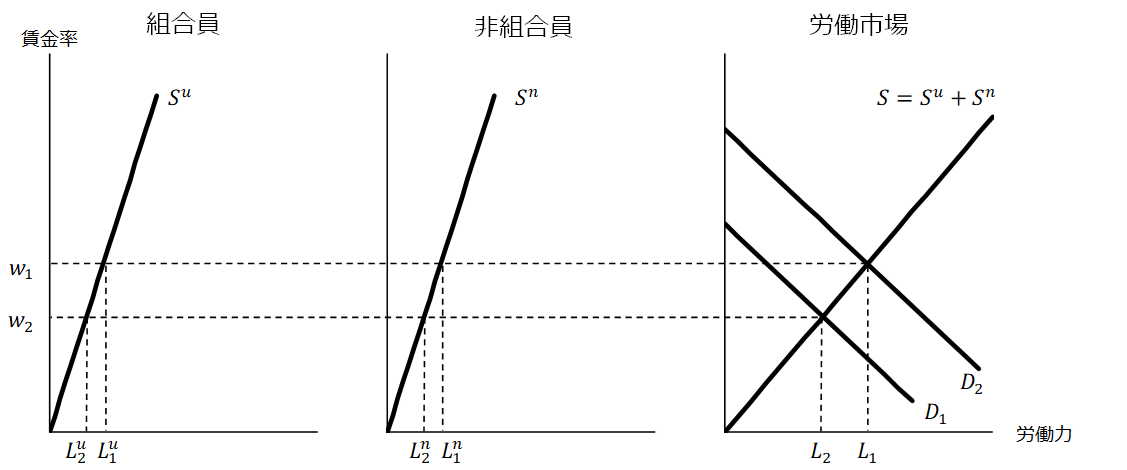
　上図のように、労働市場において組合員と非組合員が存在する状況を考える。このとき、 $S^u$ は組合員の労働供給曲線、 $S^n$ は非組合員の労働供給曲線、そして $S$ は組合員および非組合員を合わせた市場全体の労働曲線を表している。また $D_1$ が産業全体の労働需要曲線を表すものとする。
　組合員と非組合員の双方で労働市場が均衡しており、失業は発生していないものと仮定する。そして、均衡賃金率が $w_1,$ 組合員および非組合員の雇用がそれぞれ $L_1^u,L_1^n$ で、労働市場全体の雇用労働力が $L_1=L_1^u+L_1^n$ に決定されているとする。
　このような状況で、この産業に対するマイナスの需要ショックが発生し、労働需要曲線が $D_1$ から $D_2$ へと左下方向へ移動したとしよう。このとき、 $w_2$ にまで賃金率が低下したら、組合員および非組合員の雇用はそれぞれ $L_2^u,L_2^n$ へと減少して再度均衡に至る。
　このとき、もし労働組合が賃金の引き下げに同意しなかった場合、組合員の賃金率は $w_1$ で雇用労働力は $L_1^u$ のままである。もし非組合員にも同じ賃金率 $w_1$ を支払わなければならないのであれば、非組合員に失業が発生する（賃金率が $w_1$ であれば、非組合員も $L_1^n$ の労働供給を望むものの、市場全体での労働需要が減少しているため、雇用を希望する非組合員の全員が雇用されることはないためである。）。
　他方、もし非組合員に組合員よりも低い賃金を支払うことが認められるのであれば、再度非組合員の失業は解消する。 $w_1,w_2$ よりも低水準の賃金を支払うことで、非組合員の労働供給が減少し、非組合員の労働力の需給が一致するためである。このため、この理論で実質賃金の下方硬直性と失業を説明するには、強い交渉力を持つ労働組合が存在し、同一労働を行う労働者に対する賃金差別が存在することは禁止されなければならない。
　企業全体が労働市場の均衡水準よりも高い水準の賃金を支払うことで労働者の生産性向上を図る場合、これよりも低水準の賃金での雇用を求める労働者の申し出を企業は受け入れない。このような理由で賃金の下方硬直性と失業が発生するとの仮説を効率賃金仮説という。

10.3.3　労働者と企業のミスマッチによる失業

　失業が発生する理由は、労働者と企業との間で互いに希望が折り合わないことかもしれない。このように発生する失業には、摩擦的失業と構造的失業が存在する。
　摩擦的失業とは、求人（労働需要）自体は存在するものの、労働者側がその条件を受け入れずに休職し続けることで発生する失業をいう。これに対し、新たな仕事が存在するのは分かっているものの、その仕事に就くための費用が大きすぎて仕事に就くことができないために発生する失業を構造的失業という。

　では、なぜこのような失業が発生するのか。それを説明する仮説にジョブ・サーチ理論と部門間移動仮説がある。
　ジョブ・サーチ理論は、求職者が労働市場に関して不完全な情報しか持たないことが失業の原因だと考える。雇用に関する情報を獲得するにはコストがかかるため、すべての情報を獲得しての求職活動は最適ではない。そこで求職者（家計）は、ある求人において納得する水準の賃金を提示されれば、その仕事を受け入れ求職活動を終了する。賃金水準が折り合わず、より高額の賃金を提示する企業が存在し得ると求職者が考えれば、求職者はその求人を謝絶し、次の求人を探索する。家計が提示された賃金を受け入れるまで、この過程は継続する。
　家計が受け入れる際の条件をより詳しくみていく。求職者が求人を受け入れるのは、別の仕事で得られ得る賃金（期待賃金）が求職活動に必要な費用を下回る場合である。求職者が求職活動を停止するような賃金の最低水準（留保賃金）が高くなれば、求職活動期間も長期化することになるため、摩擦的失業は増大することになる*1。

　留保賃金は、

求職者の能力や保有資産
より良い提示賃金の仕事を獲得し得る確率

が関係する。そのため、求職者数や企業の求人数の多さが、新たな就業者が生まれる確率を高めると考えられる。そこで、ある時点 $t$ における新たな就業者数 $M_t$ は、失業者 $U_t$ と求人者数 $V_t$ によって、以下のようなマッチング関数にて定まると仮定しよう。

$\begin{aligned} M_t=M(U_t,V_t)=\alpha {U_t}^{\beta}{V_t}^{1-\beta}, 0\lt\alpha,\beta\lt1 \end{aligned}$

　両辺を $U_t$ で割ることで、

$\begin{aligned} &\displaystyle{\frac{M_t}{U_t}}=\alpha {U_t}^{\beta-1}{V_t}^{1-\beta}\\ \Leftrightarrow&\displaystyle{\frac{M_t}{U_t}}=\alpha\left(\displaystyle{\frac{V_t}{U_t}}\right)^{1-\beta}\\ \end{aligned}$

と変形できる。これは、求職者1人当たりの求人数( $V_t/U_t$ )が増えれば、失業者が仕事を見つける確率に相当する $M_t/U_t$ が高まることを意味する。

　次に、この関数を用いて定常状態における失業率を考える。ある時点における就業者を $E_t$ 、就業者が失業者になる確率を $q$ とすれば、

$\begin{aligned} E_{t+1}=(1-q)E_t+M_t \end{aligned}$

が成り立つ。労働力人口について $X_t\equiv X$ 、すなわち時間を通じて一定であると仮定すれば、

$\begin{aligned} &{}^{\forall}t\left(X=E_t+U_t\right)\\ \Leftrightarrow&{}^{\forall}t\left(E_t=X-U_t\right)\\ \Leftrightarrow&{}^{\forall}t\left(\displaystyle{\frac{E_t}{X}}=1-\displaystyle{\frac{U_t}{X}}\right) \end{aligned}$

であるから、

$\begin{aligned} &E_{t+1}=(1-q)E_t+M_t\\ \Leftrightarrow&\displaystyle{\frac{E_{t+1}}{X}}=(1-q)\displaystyle{\frac{E_t}{X}}+\displaystyle{\frac{M_t}{X}}\\ \Leftrightarrow&\displaystyle{\frac{E_{t+1}}{X}}=(1-q)\displaystyle{\frac{E_t}{X}}+\displaystyle{\frac{M_t}{U_t}}\displaystyle{\frac{U_t}{X}}\\ \Leftrightarrow&\displaystyle{\frac{E_{t+1}}{X}}=(1-q)\displaystyle{\frac{E_t}{X}}+\alpha\left(\displaystyle{\frac{V_t}{U_t}}\right)^{1-\beta}\displaystyle{\frac{U_t}{X}}\\ \Leftrightarrow&1-\displaystyle{\frac{U_t}{X}}=(1-q)\left(1-\displaystyle{\frac{U_t}{X}}\right)+\alpha\left(\displaystyle{\frac{V_t}{U_t}}\right)^{1-\beta}\displaystyle{\frac{U_t}{X}} \end{aligned}$

が得られる。 $u_t\equiv\displaystyle{\frac{U_t}{X}}$ とすれば、

$\begin{aligned} 1-u_{t+1}=(1-q)(1-u_t)+\alpha\left(\displaystyle{\frac{V_t}{U_t}}\right)^{1-\beta}u_t \end{aligned}$

と書き換えることができる。この $u_t$ を完全失業率と呼ぶ。
　定常状態では、 $u_{t+1}=u_t\equiv u^{*}$ であり、また $V_t/U_t\rightarrow V/U$ (一定)だと考えられるから、

$\begin{aligned} &1-u^{*}=(1-q)(1-u^{*})+\alpha\left(\displaystyle{\frac{V}{U}}\right)^{1-\beta}u^{*}\\ \Leftrightarrow&q(1-u^{*})=\alpha\left(\displaystyle{\frac{V}{U}}\right)^{1-\beta}u^{*}\\ \end{aligned}$

である。 $\gamma\equiv\alpha\left(\displaystyle{\frac{V}{U}}\right)^{1-\beta}$ とおけば、

$\begin{aligned} &q(1-u^{*})=\gamma u^{*}\\ \Leftrightarrow&(q+\gamma)u^{*}=q\\ \Leftrightarrow&u^{*}=\displaystyle{\frac{q}{q+\gamma}}\\ \Leftrightarrow&u^{*}=1-\displaystyle{\frac{\gamma}{q+\gamma}} \end{aligned}$

を得る。
　ここから、次のような命題が得られる：

就業者が失業する確率 $q$ が高まると、完全失業率 $u^{*}$ は増加する
求職者1人当たりの求人数 $V/U$ が高まると、完全失業率 $u^{*}$ は低下する

　部門間移動仮説は、構造的失業を説明するのに考えられた。構造的失業は労働者の産業（部門）間の移動が困難なために生じる失業である。何らかのショックが発生した場合、部門や産業によって、正のショック（労働需要が増大するショック）が発生するところがあれば、負のショック（労働需要が減少するショック）が発生するところもある。制約がなければそうした部門・産業間で雇用の移動が発生するはずであるが、実際には転職コストを伴う。場合によっては転職を諦める場合もあり得る。

10.3.4　実質賃金の下方硬直性とミスマッチの深刻さ

　実質賃金の下方硬直性による失業とミスマッチによる失業がどの程度存在するのかを知るためには $\mathrm{UV}$ 曲線（ベバレッジ曲線）を見ればよい。ベバレッジ曲線は、求職者（または失業率）を横軸に、求人数（欠員率）を縦軸に取り、両者の相関関係を表したものである。ここで、

$\begin{aligned} 欠員率&=\displaystyle{\frac{有効求人数-就職件数}{有効求人数-就職件数+雇用者数}}\\ 雇用失業率&=\displaystyle{\frac{完全失業者}{完全失業者+雇用者数}} \end{aligned}$

で定義する。

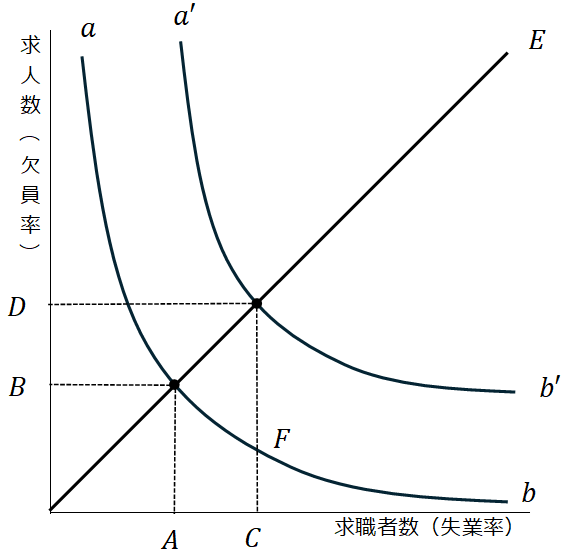
　もし労働需要と供給のミスマッチで失業が生じるならば、求職数と求人数の関係は直線 $\mathrm{OE}$ 上を移動する。これにより曲線 $\mathrm{ab}$ から曲線 $\mathrm{a^{'}b^{'}}$ にベバレッジ曲線へ変化した場合、求職数は $\mathrm{OC}$ 、求人数は $\mathrm{OD}$ へと変化する。
　ベバレッジ曲線が示すように、現実の失業原因を実質賃金の下方硬直性のみに求めるのは難しい。賃金が硬直的であっても、好況になれば労働需要が増加して労働市場は均衡し、失業は解消されうるはずである。しかし、2000年代の先進国では好況期の失業率の大幅な低下は観測されていない。
　一方、労働市場の均衡を前提として、ミスマッチだけで現実の失業を説明することも難しい。

　失業対策のための経済政策は、原因によって異なる。ただし、このような分類が常に正しいとは限らない。

	実質賃金の下方硬直性	下方硬直性が直ちに解消できない場合、財政支出の増加や金融緩和策によって景気を刺激し、労働需要を高める。
	ミスマッチ	景気刺激策では失業は解消しえず、ミスマッチを減少させるためにハローワークの充実や職業訓練が必要である。

10.4　日本の失業に関する実証研究

10.4.1　インサイダー・アウトサイダー理論

　日本でのインサイダー・アウトサイダー理論を実証したのは $\mathrm{Yamane}$ (1998)がはじめてである。そこでは、インサイダー・アウトサイダー理論は日本の失業率の持続性を説明できないという結論が得られている。それは、日本では少なくとも「同一労働同一賃金」が成立していないことが理由とされる。

10.4.2　効率賃金仮説

　日本を対象とした効率賃金仮説に関する実証研究は少ない。

10.4.3　ジョブ・サーチ理論

　日本でも「シャイマーのパズル」*2が成り立つことが知られている。また、企業に固有の訓練を考慮すると、説明力が改善することも知られている。

10.4.4　構造的失業

　日本でミスマッチによる失業が増加したのは2000年代に入ってからで、それまではミスマッチによる失業は大きく変化していない。もっとも、日本で構造的失業が存在しなかったわけではない。

10.4.5　失業の流出入

　失業率の変化は、就業者や非労働力から失業者への流入と、失業者から就業者や非労働力への流出の差で決定される。この両者の動きと景気との関係性を考える。
　1つには、就業者から失業者への流入率は景気と逆相関的で、失業者から就業者への流入率は景気と順相関的である。また失業率の変動を説明する要因として、日本では離職率が相対的に重要である。

次回

準備中

問題*3

1.　家計の労働供給

　家計の労働供給について以下の問いに答えよ。家計の効用関数を

$\begin{aligned}U=U(C,H)=\log C+\log H\end{aligned}$

とする。

(a) この家計が所得を労働からの収入に完全に依存していると仮定する。消費を $C$ 、余暇を $H$ 、労働時間を $L$ 、労働ないし余暇の時間の上限を $\bar{L}$ とし、 $W$ を名目賃金率、 $P$ を消費財価格とする。この家計が選択する $L$ を求めよ。また $W,P$ それぞれが変化したときに $L$ がどのように動くのかを説明せよ。
(b) この家計が選択する $C$ を求めよ。

2.　企業の労働需要

　企業の労働需要に関して、生産関数を $F(L)=L^{\alpha},0\lt\alpha\lt1$ と仮定する。

(a) この企業の利潤関数を示せ。なお、消費を $C$ 、余暇を $H$ 、労働時間を $L$ 、労働ないし余暇の時間の上限を $\bar{L}$ とし、 $W$ を名目賃金率、 $P$ を消費財価格とする。
(b) この企業にとって最適な労働需要量 $L^{*}$ を示せ。また、 $P,W$ が変化すると $L^{*}$ はどのように変化するか。

3.　労働需給関数

　労働供給関数が $L^{S}=4+4(W/P)$ 、労働需要関数が $L^{D}=24-(W/P)$ であることを仮定する。ここで $(W/P)$ は実質賃金率である。

(a)均衡実質賃金率 $(W/P)^{*}$ および均衡労働雇用量 $L^{*}$ を求めよ。
(b)失業が10発生している場合の実質賃金率 $(W/P)$ を求めよ。

4.　マッチング関数

　マッチング関数が

$\begin{aligned}M_t=M(U_t,V_t)=\alpha{U_t}^{\beta}{V_t}^{1-\beta}\end{aligned}$

で与えられると仮定する。

(a) $\alpha=0.1,$ $\beta=0.5,$ $U_t=4000,$ $V_t=1000$ の場合、失業者が仕事を見つける確率 $M_t/U_t$ を求めよ。
(b)ある時点 $t$ における就業者を $E_t,$ 就業者が失業者になる確率を $q$ で表す。 $E_t=16000,$ $q=0.03$ の場合、 $E_{t+1}$ はいくらか。またこの時点における失業率 $u_t$ を求めよ。
(c) 定常状態の失業率 $u^{*}$ を求めよ。

5.　労働組合の有無

　ある経済には労働組合に所属する労働者と労働組合に属さない労働者が存在する。労働組合員の労働供給関数は $L_S^U=\displaystyle{\frac{w}{2}},$ 非労働組合員の労働供給関数は $L_S^N=\displaystyle{\frac{w}{2}}$ であるとき、以下の問いに応えよ。

(a)この経済全体の労働供給関数を求めよ。
(b)経済全体の労働需要関数が $L_D=1000-w$ であると仮定する。このときの均衡賃金と組合員および非組合員の雇用量を求めよ。
(c)経済に負のショックが生じ、労働需要曲線が $L_D=800-w$ にシフトした。このときの均衡賃金と組合員および非組合員の雇用量を求めよ。
(d)労働組合は組合員の賃金と雇用を(b)の解から引き下げることに反対し、結果的に企業は組合員の賃金も雇用も引き下げることができなかった。このとき、非組合員の失業者は何人になっているか。
(e)非組合員が賃金の引き下げに応じることで失業を回避した。(c)の企業が雇用する労働を維持したまま賃金を引き下げる場合、非組合員の賃金をいくらに設定したら失業は解消されるか。