時系列解析の基礎(01/XX) - 「大人の教養・知識・気付き」を伸ばすブログ

　以下の書籍

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

作者:竜義, 沖本
朝倉書店

Amazon

を中心に時系列解析を勉強していきます。

※2022年7月8日　加筆しました。

1.　時系列解析の基礎
次回
参考文献

1.　時系列解析の基礎

　時系列(データ)とは時間の順序に従って並べられたデータを指す。ある一定の時間間隔で観測されたものもあれば、連続的な時間で観測されたものもある。不規則な時間間隔で観測された時系列も存在する。

　時系列解析とはそうした時系列に対して、関心のある事象における過去・現在・未来の値を適切に把握・推計し、関連してその結果をもとに事象の仕組みや影響に関する知見を得たり対策を考えたりする分析である。

　時系列解析のアプローチには、（1）確定的な方法、（2）確率的な方法の2つがある。

　時系列解析を行うにあたっての問題が1つある。それは各時点における実現値を1つしか観測できないということである。特に期待値などの統計量を計算する際にはそれらが時点に依存し得るために各時点の観測数問題は大きな問題となる。そこでそうした観測値を確率変数列 $\{y_t\}_{t=-\infty}^{\infty}$ から得られた1つの実現値と見なし、その確率変数列の生成構造について何らかの性質や構造を仮定する。確率変数の時間による系列を確率過程（stochastic process）といい $\{y_t\}$ と書く。この確率過程は時点によって順序付けられていることで通常の確率とは相違する。

1.1　時系列解析の目的

1.1.1　時系列解析の必要性

　確率過程（時系列解析）の解析とそれとの対比の意味での統計学との差異はデータ間の独立性を考えるのか否かにある。前者はデータ間に従属性があることを前提にして解析するものである。これに対して後者は最尤推定を典型例としてデータを独立したものと考えるのが自然である。したがって解析するときに各データ間に如何なる関係を考えるのかに応じて解析することとなる。

時系列解析

あり←　　

データ間の相関が…

　　→なし

統計学

1.1.2　時系列解析の目的

　時系列解析で議論する問題は4つに大別できる：

	記述・可視化	時系列を図示したり、標本自己相関関数やピリオドグラム(後述)などを用いて時系列の特徴を簡潔に表現する。
	モデリング	与えられた時系列に対してその変動の仕方を表現する時系列モデルを推定し、時系列の確率構造を解析する。
	予測・シミュレーション	現在までに得られた情報から今後の変動を予測する。
	信号抽出	時系列から目的に応じて必要な信号や情報を取り出す。

1.1.3　時系列解析における推計

　時系列解析における推計は3つに分類できる：

平滑化（スムージング）：過去の時点に対する推計
フィルタリング（濾波）：現在の時点に対する推計
予測：未来の時点に対する推計

　平滑化はさらに3つのものに分類できる：

	(1)固定区間平滑化	推計時点に対して現在までの全データを考慮する。
	(2)固定ラグ平滑化	推計時点に対して少し先までの観測データのみを考慮する。
	(3)固定点平滑化	特定の時点のみに着目する。

1.2　時系列データの種類

　時系列は様々な観点から類別することができる。
　まず前述のように連続時間か否かで分類できる。また1変量なのか多変量なのかも相違し、時系列分布が正規分布に従う(ガウス型時系列な)のかでも分類できる。また線形モデルの出力として表現できる時系列を線形時系列と呼ぶ。

1.3.　時系列データの前処理

　その性質を抽出しやすくすることなどの様々な理由から、時系列データは観測したそのままのデータを使うこともあれば、それを加工したものを元のデータと見なして扱うこともある。

	(1)原系列	$y_t$
	(2-1)変数変換：対数系列	$\log y_t$
	(2-2)変数変換：ロジット変換	$\log\left(\displaystyle{\frac{y_t}{1-y_t}}\right)$
	(3)( $n$ 次)差分系列	$y_t-y_{t-n}$
	(4)前期比、前年同期比	$\displaystyle{\frac{y_t}{y_{t-1}}}$
	(5)( $n$ 次)対数差分列	$\log y_t-\log y_{t-n}$
	(6-1)(前後 $k$ 期)移動平均	$T_n=\displaystyle{\frac{1}{2k+1}\sum_{j=-k}^{k}y_{n+j}}$
	(6-2)(前後 $k$ 期)移動平均	$T_n=\displaystyle{\sum_{j=-k}^{k}\omega_jy_{n+j}},\displaystyle{\sum_{j=-k}^{k}\omega_j}=1,\omega_j\geq0$
	(6-3)(前後 $k$ 期)移動メディアン	$T_n=\mathrm{median}\left\{y_{n-k},y_{n-k+1},\cdots,y_{n+k}\right\}$

　時系列データそのもの、すなわち

$\begin{aligned} y_t \end{aligned}$

を原系列と呼ぶ。
　また頻用される加工手法によってはその加工を行ったデータにそれぞれ名前がついている。たとえば後述する定常性を確保するために対数変換を行うことがあり、対数変換を行った原系列

$\begin{aligned} \log{y_t} \end{aligned}$

を対数系列と呼び $\log⁡{y_t}$ と書く。また前時点との差分を取った

$\begin{aligned} \Delta y_t=y_t-y_{t-1} \end{aligned}$

を差分系列（階差系列）と呼ぶ。また成長率（増減率）を議論するために対数差分列

$\begin{aligned} \Delta \log⁡{y_t}=\log{y_t}-\log{y_{t-1} } \end{aligned}$

を用いることも多い *1。
　それ以外に特に経済データの場合、季節変動を削除したデータを季節調整済系列と呼ぶ。

1.4　基本統計量と時系列モデル

　時系列解析でも一般の統計解析と同様に最初は基本統計量の計算を通じたデータの要約を行う。それを通じてデータの背後にある構造の特徴を抽出するのである。まず最も基本的な統計量は期待値（平均）である。また分散を用いてある一時点におけるバラつきの尺度として用いる。
　他方で時点の相違とデータのバラつきを考えるための基本統計量が時系列解析に特有の統計量として存在する。確率過程 $\{X_t\}$ の自己共分散は時点をズラした自分自身との共分散であり、時点 $t$ とラグ $k$ の関数

$\begin{aligned} \mathrm{Cov}[ X_t,X_{t-k}]=E [(X_t-E[ X_t ])(X_{t-k}-E[X_{t-k}])] \end{aligned}$

と定義される。
　またこれを時点 $t$ および $t-k$ の分散を用いて規格化したものを自己相関係数という。

$\begin{aligned} \rho_{t,k}=\displaystyle{\frac{\mathrm{Cov}[X_t,X_{t-k}]}{\sqrt{V[X_{t}]}\sqrt{V[X_{t-k}]}}} \end{aligned}$

自己共分散関数と自己相関関数　確率過程 $\{X_t\}$ に対してラグ $k\in\mathbb{N}$ の自己共分散関数 $\gamma(y_t,k)$ は

$\begin{aligned} \gamma(y_t,k)=\mathrm{Cov}[ X_t,X_{t-k}]=E [(X_t-E[ X_t ])(X_{t-k}-E[X_{t-k}])] \end{aligned}$

で定義される。またラグ $k\in\mathbb{N}$ の自己相関関数 $\rho(y_t,k)$ は

$\begin{aligned} \rho(y_t,k)=\displaystyle{\frac{\mathrm{Cov}[X_t,X_{t-k}]}{\sqrt{V[X_{t}]}\sqrt{V[X_{t-k}]}}} \end{aligned}$

で定義される。

　通常の相関係数と同様に、 $-1\leq \rho_{t,k}\leq1$ と確かに規格化できていることを確認できる。実際に $X_t$ の分布関数を $f(x)$ とすれば $\mathrm{Cauchy}$ - $\mathrm{Schwartz}$ の不等式を用いることで

$\begin{aligned} V[X_t]V[X_{t-k}]&=\left(\int_{-\infty}^{\infty} (x-E[X_t])^{2}f(x)dx\right) \cdot \left(\int_{-\infty}^{\infty} (x-E[X_{t-k}])^{2}f(x) dx\right) \\ &\geq \left(\int_{-\infty}^{\infty}(x-E[X_t])(x-E[X_{t-k}])f(x)dx\right)^{2} \end{aligned}$

(右辺) $=(\mathrm{Cov}[X_t,X_{t-k}])^2$ に注意すれば $\mathrm{Cov}[X_t,X_{t-k}]=C$ とおいて

$\begin{aligned} \left|C\right| &\leq \sqrt{V[X_t]} \cdot \sqrt{V[X_{t-k}]} \\ \therefore& -1 \leq \frac{\mathrm{Cov}[X_t,X_{t-k}]}{\sqrt{V[X_t]}\sqrt{V[X_{t-k}]}} \leq 1 \end{aligned}$

また $k=0$ ならば明らかに自己相関係数は $1$ である。
　上記の自己相関係数は対象とする時点以外の変量の間接的な相関を含む。そのような間接的な相関を射影により除いた直接的な相関を偏自己相関係数という*2。ラグ $h$ の偏自己相関 $\phi_{hh}$ は以下の方程式を解くことで得られる：

$\begin{aligned} \begin{bmatrix} \phi_{h1}\\ \phi_{h2}\\ \vdots\\ \phi_{hh} \end{bmatrix}=\begin{bmatrix} 1&\rho_1&\cdots&\rho_{h-1}\\ \rho_1&1&\cdots&\rho_{h-2}\\ \vdots&\vdots&\ddots&\vdots\\ \rho_{h-1}&\rho_{h-2}&\cdots&1 \end{bmatrix} \begin{bmatrix} \rho_1\\ \rho_2\\ \vdots\\ \rho_h \end{bmatrix} \end{aligned}$

　さて以上は理論的な概念であるが、実際の解析では観測値からそれらを推定することが必要となってくる。平均、自己共分散、自己相関係数の自然な推定量として

$\begin{aligned} \bar{y}&=\frac{1}{T}\sum_{t=1}^{T}y_{t}, \\ \hat{\gamma}_{k}&=\frac{1}{T}\sum_{t=1}^{T}(y_{t}-\bar{y})(y_{t-k}-\bar{y}), \\ \hat{\rho}_{k}&=\frac{\hat{\gamma}_{k}}{\hat{\gamma}_{0}} \end{aligned}$

を用い、それぞれ標本平均、標本自己共分散、標本自己相関係数という*3。

1.5　定常性

　時系列解析が他の統計解析と最も異なる点は、観測値に順序があること、すなわち時間の流れに沿って出現した値を扱う点である。そのため、実時間では繰り返しの観測ができず、1本の標本系列( $\mathrm{sample\ path}$ )のみから統計的推測を行なう必要がある。この問題を解決するために定常性を仮定することになる。
　確率過程においてその確率的な性質が変わらないという特徴を定常性という。定常性は(条件の)強さに応じて2つに分類される：

	(1)	強定常	確率分布が時点 $t$ に依存せず変わらない、すなわち任意の $t,k$ に対して $(y_t,\cdots,y_{t+k})^T$ の同時分布が等しい。
	(2)	弱定常	期待値と自己共分散が時点に依存しない、すなわち任意の $t,k$ に対して $\begin{aligned}E[X_t]&=\mu,\\\mathrm{Cov}[X_t,X_{t-k}]&=\gamma_k\gt0\end{aligned}$ が成り立つ。

　定義から明らかに強定常ならば弱定常であるが逆は成り立たない。また弱定常であるとき任意の $t,k$ に対して $t^{\prime}=t-k$ とおけば

$\begin{aligned} \gamma_{k} &=\mathrm{Cov}[X_t,X_{t-k}]\\ &=\mathrm{Cov}[X_{t^{\prime}+k},X_{(t^{\prime}+k)-k} ] \\ &=\mathrm{Cov}[X_{t^{\prime}+k},X_{t^{\prime}} ] \\ &=\mathrm{Cov}[X_{t^{\prime}},X_{t^{\prime}+k} ] \\ &=\gamma_{-k} \end{aligned}$

である。すなわち $\gamma_k=\gamma_{-k}$ であり、したがって $\rho_{t,k}=\rho_{t,-k}$ である。弱定常過程に従う時系列は、時間が経過しても変わらずに同じように発生するような値の系列である。
　任意の $s\neq t$ で $E[X_s\bar{X}_t]=0,$ すなわち $h\neq0$ ならば $\gamma_h=0$ であるとき、 $\{X_t\}$ は直交過程と呼ばれる。直交とは、確率変数 $X,Y$ に対する内積およびノルムを

$\begin{aligned} \langle X,Y \rangle=E\left[X\bar{Y}\right], \left\|X\right\|=E|X|^2 \end{aligned}$

で定義するとき、 $E[X_s\bar{X}_t]=0$ は $X_s,X_t$ の直交を意味するからである*4。
　強定常であれば時系列解析を行う意義は薄い。そのため通常、弱定常性の有無の方が重要な検討対象となる。実際、強定常過程の典型例が $i.i.d.$ 系列、すなわち各時点のデータが互いに独立かつ同一の分布に従うような確率過程であるが、このような過程ではそもそも時点の相違を考慮する意義が薄く通常の統計解析でも十分である。定常性を持たない確率過程を非定常過程と呼ぶ。
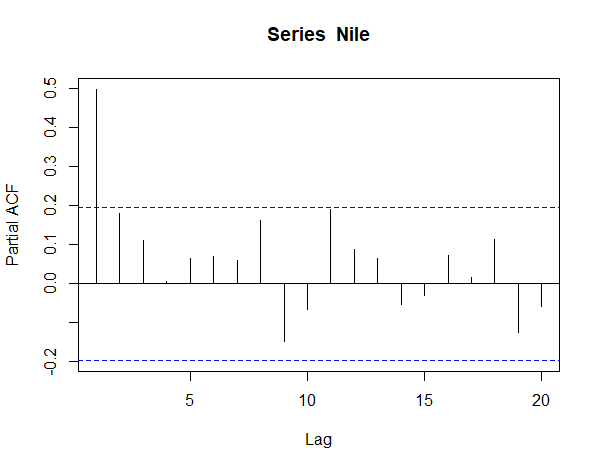
　定常性を確認するための一つの手段として、ラグを横軸、標本自己相関係数を縦軸としたグラフを作成し目視するものがある。このグラフをコレログラムという。

1.6　Rでのサンプルスクリプト

　 $\mathrm{R}$ を用いて $\mathrm{Nile}$ を分析する。

##############################
### Nileを用いた時系列解析 ###
##############################

### まずは基礎分析
library("ggplot2")

# データ
data("Nile")

# データの確認
head(Nile)

## グラフ化
df_Nile <- data.frame(year = seq(start(Nile)[1],end(Nile)[1]),
                      value = as.numeric(Nile))

g <- ggplot(df_Nile,aes(x = year, y = value)) + geom_line()
g <- g + theme_classic() + scale_y_continuous(breaks = c(0,250,500,750,1000,1250,1500))
g <- g + geom_hline(yintercept = 0, linetype = 3, alpha = 0.9) + 
  geom_hline(yintercept = 250, linetype = 3, alpha = 0.5) + 
  geom_hline(yintercept = 500, linetype = 3, alpha = 0.5) + 
  geom_hline(yintercept = 750, linetype = 3, alpha = 0.5) + 
  geom_hline(yintercept = 1000, linetype = 3, alpha = 0.5) + 
  geom_hline(yintercept = 1250, linetype = 3, alpha = 0.5) + 
  geom_hline(yintercept = 1500, linetype = 3, alpha = 0.5)
plot(g)

## 原系列
Nile

## 差分系列
diff(x = Nile,lag = 1)

## 対数系列
log(Nile)

## 対数差分系列
diff(x = log(Nile),lag = 1)

# 統計量
nm_mean <- mean(Nile)
nm_sd <- sd(Nile)
vc_acv <- as.vector(acf(Nile,type = "covariance",plot = F)$acf)[1:10]
vc_acf <- as.vector(acf(Nile,type = "correlation",plot = F)$acf)[1:10]
vc_pacf <- as.vector(pacf(Nile,type = "correlation", plot = F)$acf)[1:10]

# コレログラフ
acf(Nile,type = "covariance",plot = T)
acf(Nile,type = "correlation",plot = T)
pacf(Nile,plot = T)

Nileのコレログラフ(左:自己共分散/中央:自己相関係数/右:偏自己相関係数)

次回

power-of-awareness.com

参考文献

沖本竜義(2010)「経済・ファイナンスデータの計量時系列分析」(朝倉書店)
北川源四郎(2020)「Rによる時系列モデリング入門」（岩波書店）
柴田里程(2017)「時系列解析」(共立出版)
白石博(2022)「時系列データ解析」(森北出版)
萩原淳一郎，瓜生真也，牧山幸史[著]，石田基広[監修](2018)「基礎からわかる時系列分析　Rで実践するカルマンフィルタ・MCMC・粒子フィルタ」(技術評論社)

*1:対数差分を用いるのは、変化分があまり大きくなければTaylor展開より通常の変化率と近似的に一致するうえ、連続時間であれば正確に瞬時的な変化率に一致するからである。また対数変換を行ったうえで差分を取れば対数差分は計算できるが、一般にコンピュータでの計算では乗算や除算の方が加算・減算よりも時間がかかることも理由の1つである。さらに対数系列でのメリットである定常性の確保が可能になることもある

*2:ただし間接的な相関を線形結合の形で除外したのみであるため、変数間の非線形な関係に基づく相関は除外できない。

*3:標本自己共分散に不偏性を求めるならば $t-k$ で割るべきであるが、 $k$ が大きくなったときに推定値が不安定になることを避け、また分かりやすさが出ることから $n$ で割っている。

*4: $E|X|^2$ は確率変数の絶対値の二乗に対して期待値を取ることを意味する。

1. 時系列解析の基礎

1.1 時系列解析の目的

1.1.1 時系列解析の必要性

1.1.2 時系列解析の目的

1.1.3 時系列解析における推計

1.2 時系列データの種類

1.3. 時系列データの前処理

1.4 基本統計量と時系列モデル

1.5 定常性

1.6 Rでのサンプルスクリプト

次回