時系列解析の基礎(02/XX) - 「大人の教養・知識・気付き」を伸ばすブログ

　以下の書籍

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

作者:竜義, 沖本
朝倉書店

Amazon

を中心に時系列解析を勉強していきます。

前回

power-of-awareness.com

前回
2.　スペクトル表現
3.　ARMA過程
次回
参考文献

2.　スペクトル表現

　時系列解析における典型的な道具がスペクトル表現である。時間軸を周波数軸に変換することで、個々の時間に捉われることなく、時系列に含まれる周期的な動きを明らかにすることができる。

スペクトル表現定理　　確率過程 $\{X_t;t\in T\}$ の自己共分散関数 $\gamma(t,k)=E[X_{t}\bar{X}_{t-k}]$ が

$\begin{aligned} \gamma(t,k)&=\displaystyle{\int f(t-k,\lambda)\overline{f(t,\lambda)}}d\mu(\lambda),\\ f(t,\cdot),f(t-k,\cdot)&\in\mathcal{L}^2(\Lambda,\mu),t,t-k\in T \end{aligned}$

と表現できるならば、直交増分過程 $\{W_{\lambda};\lambda\in\Lambda\}$ が存在し

$\begin{aligned} X_{t}=\displaystyle{\int_{\Lambda}f(t,\lambda)dW_{\lambda}}, t\in T \end{aligned}$

と表現できる。ここで $\mathcal{L}^2(\Lambda,\mu)$ は測度空間 $(\Lambda,\mu)$ における二乗可積分な複素数値関数から成る $\mathrm{Hilbert}$ 空間である。

　ここで直交増分過程は $\lambda_{1}\gt\lambda_{2}\gt\cdots\gt\lambda_{4}$ ならば内積

$\begin{aligned} (W_{\lambda_{1}}-W_{\lambda_{2}},W_{\lambda_{3}}-W_{\lambda_4{}})=0 \end{aligned}$

が常に成り立つような確率過程で、重複しない区間での値の増分が常に直交しているような確率過程である。
　この定理は一般の $t$ に対して成り立つ。次の定理を用いると、これを整数時点に限定し $f(t,\lambda)=e^{2\pi it\lambda}$ に取ることができ、 $X_t$ のスペクトル表現が導かれる。

三角モーメント問題　複素系列 $\{a_t;t=\cdots,-1,0,1,\cdots\}$ が $\mathrm{Hermite}$ 系列、すなわち ${}^{\forall}t\in T\left(a_{-t}=\bar{a}_t\right)$ が成り立つとき、

$\begin{aligned} a_t=\displaystyle{\int_{-\frac{1}{2}}^{\frac{1}{2}}e^{2\pi i t\lambda}d\mu(\lambda)} \end{aligned}$

が成り立つような測度 $\mu$ が存在する必要十分条件は $\{a_t\}$ が非負定符号系列であることである。ここで $\{a_t\}$ が非負定符号であるとは任意の複素数列 $\{c_t;t=1,2,\cdots,n\}$ に対して $\displaystyle{\sum_{s,t=1}^{n}c_s\bar{c}_t a_{s-t}}\geq0$ が成り立つことをいう。

　さらに $t$ が実数の場合には、

Cramérの定理　弱定常過程 $\{Z_t;t\in\mathbb{R}\}$ は、その共分散関数が連続ならば、直交増分過程 $\{W_{\lambda}\}$ で

$\begin{aligned} X_t=\displaystyle{\int_{-\infty}^{\infty}e^{2\pi i t\lambda}dW_{\lambda}} \end{aligned}$

を満たすものが存在する。

　詳細を省くと、自己共分散関数 $\gamma_h$ に関して

$\begin{aligned} \gamma_h&=\displaystyle{\int_{-\infty}^{\infty}e^{2\pi it\lambda} dF(\lambda)}\\ &=\displaystyle{\int_{-\infty}^{\infty}e^{2\pi it\lambda}f(\lambda)d\lambda} \end{aligned}$

が成り立つ。ここでの $dF(\lambda)$ は $dW_{\lambda}$ の大きさである。 $F(\lambda)$ は自己共分散関数のスペクトル表現に現れる関数というのみならず $\{X_t\}$ を $\{W_{\lambda}\}$ に変換したときの $\{W_{\lambda}\}$ の増分 $dW_{\lambda}$ の大きさという意味がある。この $F(\lambda)$ をパワースペクトル関数(スペクトル分布関数)という。また $f(\lambda)$ をスペクトル密度関数という。

################
### Spectrum ###
################

# 正規ホワイトノイズ
vc_white_noise <- rnorm(500,0,1)

ts_white_noise <- ts(vc_white_noise,frequency = 500)

ls_acf <- acf(ts_white_noise,type = "correlation",plot = F)
vc_acf <- as.vector(ls_acf$acf)
df_acf <- data.frame(lag = 0:(length(vc_acf)-1),
                     data = vc_acf)

g <- ggplot(df_acf,aes(x = lag, y = data, color = "red", fill = "red")) + geom_bar(stat = "identity") + theme_classic() 
g <- g+ theme(plot.title = element_text(hjust = 0.5),legend.position = "none",
              legend.title=element_text(size = 7),
              legend.text=element_text(size = 7))
g <- g + geom_hline(yintercept = 0, linetype = 1)
g <- g + geom_hline(yintercept = -0.25, linetype = 3) + 
  geom_hline(yintercept = 0.25, linetype = 3) + 
  geom_hline(yintercept = 0.5, linetype = 3) + 
  geom_hline(yintercept = 0.75, linetype = 3) + 
  geom_hline(yintercept = 1, linetype = 3) + scale_y_continuous(labels = seq(-0.25,1,0.25),breaks = seq(-0.25,1,0.25))
plot(g)

ls_pgram <- spec.pgram(ts_white_noise,plot = F,)

df_pgram <- data.frame(freq = ls_pgram$freq, spec = log10(ls_pgram$spec))

g <- ggplot(df_pgram,aes(x = freq, y = spec, color = "red")) + geom_line() + theme_classic() 
g <- g + labs(x ="周波数[Hz]",y="log10(スペクトル密度)")
g <- g+ theme(plot.title = element_text(hjust = 0.5),legend.position = "none",
              legend.title=element_text(size = 7),
              legend.text=element_text(size = 7))
g <- g + geom_hline(yintercept = 0, linetype = 1)
plot(g)

3.　ARMA過程

　時系列解析で焦点を当てているのは異時点間の相関であるから、それをモデルに織り込むことが論点である。相関のモデル化には2つの考え方がある。1つは異なる時点の値に共通の成分を含める方法である。もう1つの方法はある時点に過去時点の値を盛り込む方法である。前者が $\mathrm{MA}$ 過程であり後者が $\mathrm{AR}$ 過程である。実はこれらを組み合わせた $\mathrm{ARMA}$ 過程を考えることもできる。

	(1)	$\mathrm{MA}$ 過程	異なる時点の値に共通の成分を含める。
	(2)	$\mathrm{AR}$ 過程	ある時点に過去時点の値を盛り込む。

3.1　ホワイトノイズ

　時系列解析において通常の統計解析（たとえば回帰分析）での誤差項に相当する概念としてホワイトノイズ（白色雑音）を導入する。すなわち任意の $t,k$ に対して

$\begin{aligned} E[\varepsilon_t]=&0,\\ \mathrm{Cov}[\varepsilon_t, \varepsilon_{t+k}]=&\begin{cases} \sigma^2 & ,k=0\\ 0 & ,k\neq0 \end{cases} \end{aligned}$

を満たすような系列 $\{\varepsilon_t\}$ をホワイトノイズという*1。定義から明らかにホワイトノイズは弱定常である。

3.2.　MA過程

　前者の「異時点の値に共通の成分を含める方法」として移動平均モデル( $\mathrm{MA}$ 過程)がある。これは分析対象となる系列をそれより過去の各時点に生成されたホワイトノイズの線形和として表すというものである。すなわち $n$ 次 $\mathrm{MA}$ 過程は

$\begin{aligned} y_t=\mu+\varepsilon_{t}+\sum_{l=1}^{n}{\theta_{l}\varepsilon_{t-l}},\ \varepsilon_{t}\sim W.N.(\sigma^2) \end{aligned}$

と定義される*2。ホワイトノイズが弱定常過程であり、 $\mathrm{MA}$ 過程はその線形和で表されることから、 $\mathrm{MA}$ 過程は常に弱定常性を持つ。
　具体例を考えてみよう。たとえば $1$ 次 $\mathrm{MA}$ 過程は

$\begin{aligned} y_t=\mu+\varepsilon_{t}+\theta_{1}\varepsilon_{t-1},\ \varepsilon_{t}\sim W.N.(\sigma^2) \end{aligned}$

と書ける。このとき $y_{t+1}=\mu+\varepsilon_{t+1}+\theta_{1}\varepsilon_t$ となり $y_t,y_{t+1}$ がともに $\varepsilon_t$ を含むことで相関が生まれることとなる。 $y_{t+1}$ には $\varepsilon_t$ の係数である $\theta_1$ が掛かっている点に留意する必要がある。なぜならばこの $\theta_1$ が両者の相関の大きさを意味するからである。
　 $\mathrm{MA}$ 過程では確率変動をすべてホワイトノイズが決定する。またホワイトノイズの期待値が $0$ であることに注意すると

$\begin{aligned} E[y_t]&=E\left[\mu+\varepsilon_t+\sum_{l=1}^{n}{\theta_l \varepsilon_{t-l}}\right] \\ &=E[\mu]+E[\varepsilon_t]+\sum_{l=1}^{n}{\theta_l E[\varepsilon_{t-l}]} \\ &=\mu \end{aligned}$

である。また

$\begin{aligned} V[y_t]&=V\left[\mu+\varepsilon_t+\sum_{l=1}^{n}{\theta_l \varepsilon_{t-l}}\right] \\ &=V[\varepsilon_t ]+\sum_{l=1}^{n}{{\theta_l}^2 V[\varepsilon_{t-l}]} \\ &=\left(1+\displaystyle{\sum_{l=1}^{n}{\theta_l}^2}\right)\sigma^2 \end{aligned}$

が成り立つ。
　さらにラグ $k$ に対して自己共分散 $\gamma_k$ を計算する。

$\begin{aligned} \gamma_k=\mathrm{Cov}[y_t,y_{t-k}]&=\mathrm{Cov}\left[\mu+\varepsilon_t+\sum_{l=1}^{n}{\theta_l \varepsilon_{t-l}},\mu+\varepsilon_{t-k}+\sum_{l=1}^{n}{\theta_l \varepsilon_{t-k-l}}\right] \\ &=\mathrm{Cov}[\varepsilon_t+\sum_{l=1}^{n}{\theta_l \varepsilon_{t-l}},\varepsilon_{t-k}+\sum_{l=1}^n{\theta_l \varepsilon_{t-k-l}}]\\ &=\mathrm{Cov}[\varepsilon_t,\varepsilon_{t-k}]+\sum_{l=1}^{n} {\theta_l \mathrm{Cov}[\varepsilon_t,\varepsilon_{t-k-l}]} + \sum_{l=1}^{n}{\theta_l \mathrm{Cov}[\varepsilon_{t-l},\varepsilon_{t-k} ]} \\ &\ \ \ \ +\sum_{l=1}^{n}\sum_{m=1}^{n}{\theta_l\theta_m\mathrm{Cov}[\varepsilon_{t-l},\varepsilon_{t-k-m}]} \end{aligned}$

である。ここで $k\leq n$ ならば $\mathrm{Cov}[\varepsilon_t,\varepsilon_{t-k}]= \left\{ \begin{array}{} \sigma^2 & ,k=0,\\ 0 & ,k\neq 0 \end{array} \right.$ であることに注意すると

$\begin{aligned} \gamma_k&=\sum_{l=1}^{n} {\theta_l\mathrm{Cov}[\varepsilon_{t-l},\varepsilon_{t-k}} ] +\sum_{l=1}^{n}\sum_{m=1}^{n}\theta_l\theta_m\mathrm{Cov}[\varepsilon_{t-l},\varepsilon_{t-k-m}] \\ &=\theta_k \sigma^2+\sigma^2 \sum_{l=1}^{k-1}{\theta_l \theta_{k-l}} \\ &=\left(\theta_k+\sum_{l=1}^{k-1}{\theta_l \theta_{k-l}}\right) \sigma^2 \end{aligned}$

である。他方で $k\gt n$ ならばいずれの項も $0$ となるから $\gamma_k=0$ である。したがって

$\begin{aligned} \gamma_k= \left\{ \begin{array}{} (\theta_k+\displaystyle{\sum_{l=1}^{k-1}{\theta_l \theta_{k-l}}) \sigma^2}, & k\leq n,\\ 0, & k\gt n \end{array} \right. \end{aligned}$

である。
　更にここから

$\begin{aligned} \rho_k= \left\{ \begin{array}{} \displaystyle{\frac{\displaystyle{\theta_k+\sum_{l=1}^{k-1}{\theta_l \theta_{k-l}}}}{\displaystyle{1+\sum_{l=1}^{n}{\theta_l}^2} } } & ,k\leq n,\\ 0, &k\gt n \end{array} \right. \end{aligned}$

である。これらの結果から期待値はラグに依存せず定数であり、分散および自己共分散（自己相関係数）がラグにのみ依存することからMA過程は弱定常である。
　他方でMA過程は $2$ つの欠点を持つ。 $1$ つは長期の（大きい $n$ の）自己相関をモデリングするにはそれよりも多い数の観測数が必要となるため、モデル構築が実用上不便であるという点である。またMA過程はホワイトノイズの線形和で与えられるためモデルの解釈が困難であるという点である。

3.2.1　MA過程の統計量

	平均	$\begin{aligned}E[y_t]=\mu\end{aligned}$
	分散	$\begin{aligned}V[y_t]=\left(1+\displaystyle{\sum_{l=1}^{n}{\theta_l}^2}\right)\sigma^2\end{aligned}$
	自己共分散関数	$\begin{aligned}\gamma_k= \left\{ \begin{array}{}(\theta_k+\displaystyle{\sum_{l=1}^{k-1}{\theta_l \theta_{k-l}}) \sigma^2}, & k\leq n,\\0, & k\gt n \end{array} \right.\end{aligned}$
	自己相関関数	$\begin{aligned}\rho_k= \left\{ \begin{array}{}\displaystyle{\frac{\displaystyle{\theta_k+\sum_{l=1}^{k-1}{\theta_l \theta_{k-l}}}}{\displaystyle{1+\sum_{l=1}^{n}{\theta_l}^2} } } & ,k\leq n,\\0, &k\gt n \end{array} \right.\end{aligned}$

##############
### MA過程 ###
##############
set.seed(1)

vc_ma <- arima.sim(n=500, model=list(order=c(0, 0, 1), ma=c(0.8)), sd=1)

df_ma <- data.frame(date = 1:length(vc_ma),
                    MA = vc_ma)

# 図示
g <- ggplot(df_ma,aes(x = date, y = MA, color = "red")) + geom_line() + theme_classic() 
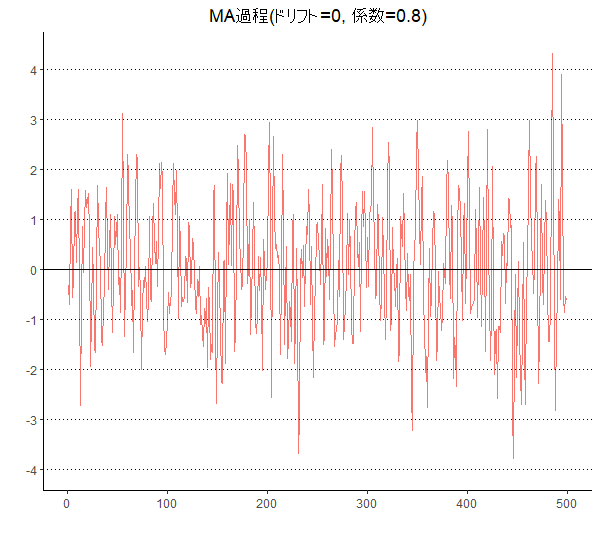
g <- g + ggtitle("MA過程(ドリフト=0, 係数=0.8)")
g <- g + labs(x ="",y="")
g <- g+ theme(plot.title = element_text(hjust = 0.5),legend.position = "none",
              legend.title=element_text(size = 7),
              legend.text=element_text(size = 7))
g <- g + geom_hline(yintercept = 0, linetype = 1)
g <- g + geom_hline(yintercept = -4, linetype = 3) + 
  geom_hline(yintercept = -3, linetype = 3) + 
  geom_hline(yintercept = -2, linetype = 3) + 
  geom_hline(yintercept = -1, linetype = 3) + 
  geom_hline(yintercept = 1, linetype = 3) + 
  geom_hline(yintercept = 2, linetype = 3) + 
  geom_hline(yintercept = 3, linetype = 3) + 
  geom_hline(yintercept = 4, linetype = 3)
g <- g + scale_y_continuous(labels = seq(-4,4,1),breaks  = seq(-4,4,1))
plot(g)

次回

power-of-awareness.com

参考文献

沖本竜義(2010)「経済・ファイナンスデータの計量時系列分析」(朝倉書店)
北川源四郎(2020)「Rによる時系列モデリング入門」（岩波書店）
柴田里程(2017)「時系列解析」(共立出版)
白石博(2022)「時系列データ解析」(森北出版)
萩原淳一郎，瓜生真也，牧山幸史[著]，石田基広[監修](2018)「基礎からわかる時系列分析　Rで実践するカルマンフィルタ・MCMC・粒子フィルタ」(技術評論社)

*1:文脈によってはホワイトノイズが正規ホワイトノイズを意味する場合がある。正規ホワイトノイズは従う分布が正規分布であるようなホワイトノイズである。

*2: $\varepsilon_{t}\sim W.N.(\sigma^2)$ は、 $\varepsilon_{t}$ が分散が $\sigma^2$ であるようなホワイトノイズであることを意味する。

前回

2. スペクトル表現

3. ARMA過程

3.1 ホワイトノイズ

3.2. MA過程

3.2.1 MA過程の統計量

次回