証券投資論（02/21） - 「大人の教養・知識・気付き」を伸ばすブログ

　証券投資（現代ポートフォリオ理論）をコンパクトに学ぶべく、比較的最近に発刊され薄めの本である

証券投資理論 (Minervaファイナンス講座)

作者:八木恭子,澤木勝茂
ミネルヴァ書房

Amazon

を参考に学んでいく。

3.　ポートフォリオ理論
- 3.1.　ポートフォリオの基本概念
- 3.2.　ポートフォリオのリスク・リターン
  - 3.2.1.　相関係数がポイント
  - 3.2.2.　ナイーブ・ポートフォリオ

前回：

power-of-awareness.com

3.　ポートフォリオ理論

3.1.　ポートフォリオの基本概念

　資産価格が変動するとそこから上がる収益（リターン）も変動する。この変動を資産のリスクという。リスク資産を組み合わせた財産目録をポートフォリオという。ポートフォリオ選択とは、リスクをある水準以下に保ちつつ、ポートフォリオの期待収益率を最大にするようなリスク資産を選択してポートフォリオを構成することを指す。ここでは、Harry Markovitzが提唱した、平均=分散モデルによるポートフォリオ選択問題を扱う。
　金融経済学の観点からでは、ポートフォリオ理論は複数の選択肢の中から意思決定者の効用関数を最大化する選択肢を選ぶ問題として発展してきた。投資家はリターンとリスクの可能な組み合わせの中から自らの効用関数を最大にするようなポートフォリオを選択する。
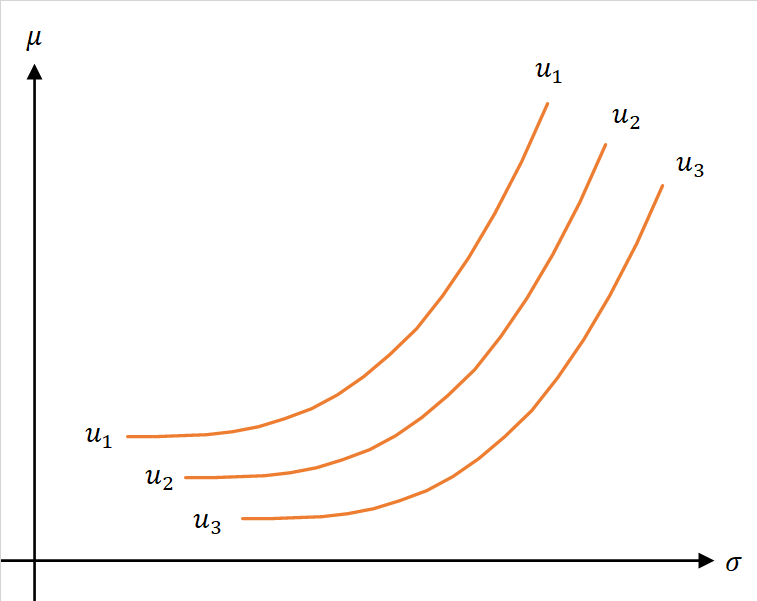
　同じ効用の値をもたらすようなリスク・リターンのペアの曲線を無差別曲線という。すなわちある投資家の効用関数を $U$ とするとき、曲線 $\{(\sigma,\mu)|U(\sigma,\mu)=U_0\in\mathbb{R}\}$ を指す。
　リスク回避を仮定すると、以下のようになる。

図表1　無差別曲線(左)とリターン・リスクによる効用*1

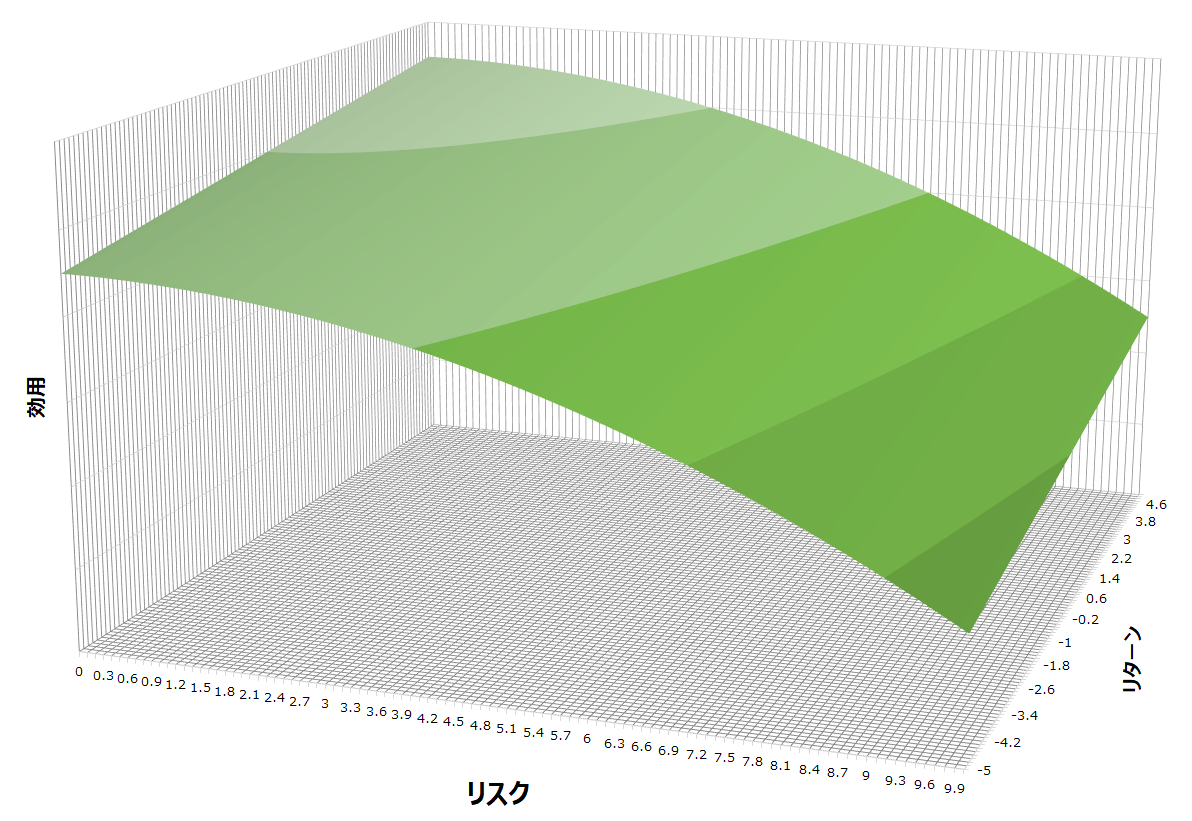
　無差別曲線は図表1の右側のグラフにおいて、 $U$ 軸のある平面 $U=U_0$ との交線を $\sigma-\mu$ 平面に射影したものを意味する。

　他方で、投資する資産およびその構成割合を確定させれば、そのポートフォリオのリスクおよびリターンが定まる。ということはそのポートフォリオの効用が確定する。このポートフォリオのリスク・リターン $\sigma_P,\mu_P$ は、投資し得る全資産の期待収益率(期待リターン)およびリスクの分散共分散行列をそれぞれ $\boldsymbol{\mu},\ \boldsymbol{\Sigma}$ 、投資ウェイトを $\boldsymbol{\omega}_P$ とすれば、

$\begin{aligned} \sigma_P=&{}^{t}\boldsymbol{\omega}_P \boldsymbol{\mu},\\ {\mu_P}^2=&{}^{t}\boldsymbol{\omega}_P \boldsymbol{\Sigma}\boldsymbol{\omega}_P \end{aligned}$

と表現できる(次章を参照せよ。)。これらを代入すれば、あるポートフォリオの効用関数は

$\begin{aligned} U(\sigma_P,\mu_P)=U({}^{t}\boldsymbol{\omega}_P \boldsymbol{\Sigma}\boldsymbol{\omega}_P,{}^{t}\boldsymbol{\omega}_P \boldsymbol{\mu})\equiv U(\boldsymbol{\omega}_P) \end{aligned}$

と投資ウェイトの関数でもある。
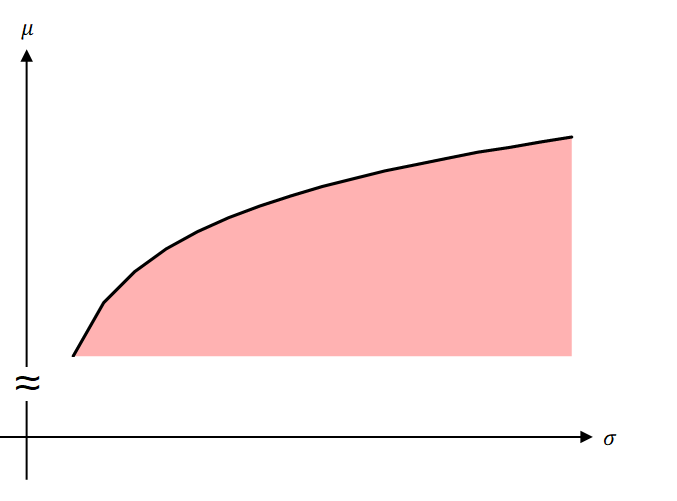
　無リスク資産に投資できるとすれば、ポートフォリオとして以下の図表2の領域(赤色部分およびその境界(黒線) )（以降、この領域を $R$ と呼ぶ。）を取り得る。

図表2　ポートフォリオが取り得るリスク=リターンの集合
f:id:suguru_125:20211211203630p:plain

こうした中で各リスクのレベルに対して最も大きなリターンを与えるようなポートフォリオを効率的ポートフォリオという。
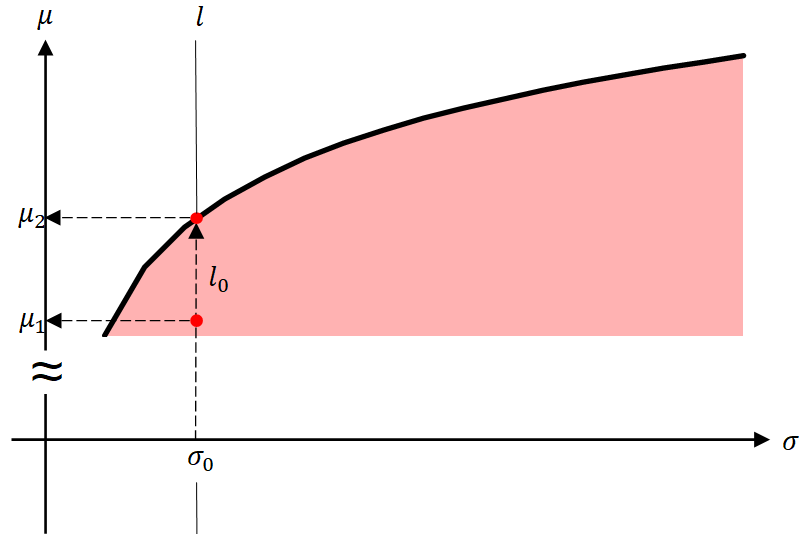
　上図表2では、効率的ポートフォリオは黒線である（以下、図表3参照）。あるリスク直線 $l:\sigma=\sigma_0$ を取ったときに、 $l$ と $R$ の交線 $l_0$ が得られる。 $l$ と領域 $R$ の境界との交点を $(\sigma_0,\mu_2)$ とする。
　この $l_0$ 上の点 $(\sigma_0,\mu_1)$ を適当に取ったとき、 $0\lt\mu_1\leq\mu_2$ が成り立つから $\mu_1=\mu_2$ のときのみ、この点は効率的である。このように考えると、効率的ポートフォリオが黒線(境界)であることが分かる。

図表3　効率的ポートフォリオ
f:id:suguru_125:20211211210605p:plain

ではこのような効率的ポートフォリオのうち、どれを選べばよいのか。そもそもの問題定式に戻れば、効率的ポートフォリオのうち効用がもっとも高いものを取ればよかった。これは以下の図表4のように、ポートフォリオの取り得る領域のうち境界に当たる部分と無差別曲線が接する点がそれに該当する。この点、すなわち「投資家の効用を最大にするような効率的ポートフォリオ」のことを最適ポートフォリオという。

図表4　最適ポートフォリオ
f:id:suguru_125:20211212012835p:plain

3.2.　ポートフォリオのリスク・リターン

　 $n$ 種類のリスク証券があるとする*2。ある期首において(最大) $n$ 種類の当該証券に投資することで期末のリターンを最大化する意思決定問題を考える。 $\omega_i$ を期初における証券 $i$ への投資ウェイトとすれば、ポートフォリオは $\boldsymbol{\omega}=(\omega_1,\cdots,\omega_n),\ \displaystyle{\sum_{i=1}^{n}\omega_i}=1$ と書ける*3。
　さて各証券 $i$ のリターン(期待リターンおよびリスク)は通常、未知である。そこでそのリターン $r_i$ を確率変数と見なし、その期待リターンおよびリスクをその母数(パラメータ)と見なす。そこで $r_i$ の分布を $F$ として、 $r_i\sim F(\mu_i,{\sigma_i}^2)$ とする。このとき、期待値および分散の性質から、ポートフォリオの期待リターンおよびリスク $\mu_P,\sigma_P$ について以下が成り立つ*4

$\begin{aligned} \sigma_P=&\displaystyle{\sum_{i=1}^{n}\omega_i}={}^{t}\boldsymbol{\omega}_P \boldsymbol{\mu},\\ {\mu_P}^2=&\displaystyle{\sum_{i=1}^{n}{\omega_i}^2 V[r_i]}+\displaystyle{\sum_{i\neq j}\omega_{i}\omega_{j} Cov[r_i,r_j]}={}^{t}\boldsymbol{\omega}_P \boldsymbol{\Sigma}\boldsymbol{\omega}_P \end{aligned}$

ここで $\boldsymbol{\omega}_P$ は考えているポートフォリオ(の投資ウェイト)である。

3.2.1.　相関係数がポイント

　証券 $i,j$ の相関係数 $\rho_{i,j}$ を導入すれば、個々の共分散 $Cov[r_i,r_j]$ は

$\begin{aligned} Cov[r_i,r_j]=\rho_{i,j}\sigma_{i}\sigma_{j} \end{aligned}$

となる。一般に相関係数 $\rho$ は $1\leq\rho\leq1$ を満たすから、相関係数の大きさ次第では、ポートフォリオとして証券を複数保有することによってそのリスク(厳密には分散)を各証券のリスク(厳密にはウェイトを加味した分散)の合算よりも小さくし得る。これはポートフォリオ内の証券を多様化させる（これを分散投資という。）ことによって、リスクを小さくし得る。これが分散投資を正当化する道理である。
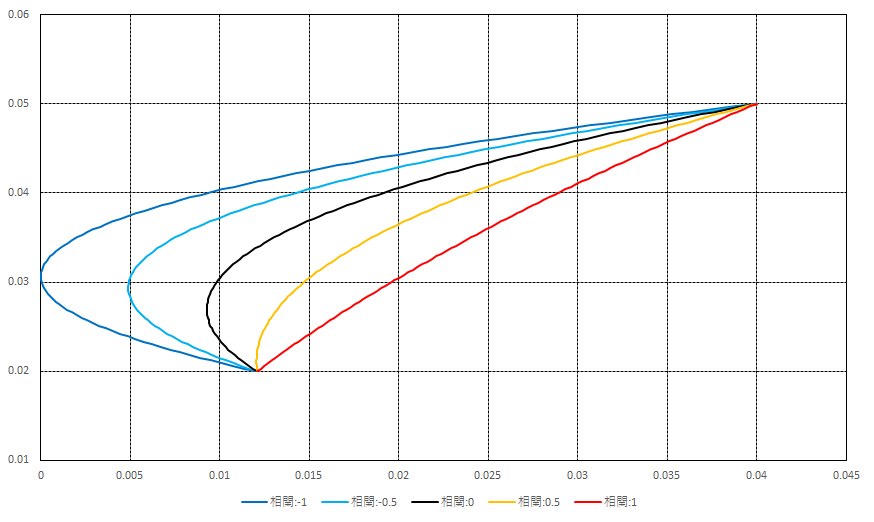
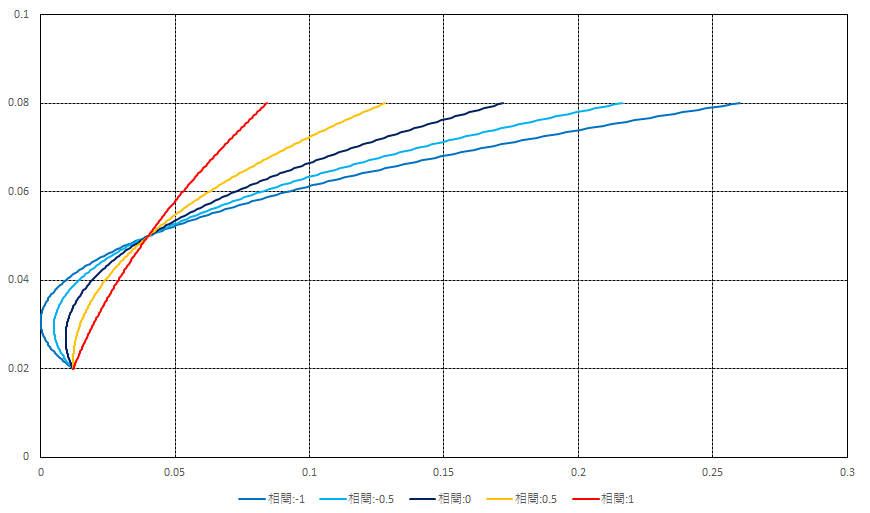
　この分散投資のミソは各証券の相関係数であった。そこで簡単のために $n=2$ としたときに相関係数の相違によるポートフォリオのリスク・リターンの関係を調べると、以下の図表5のようになる。

図表5　相関係数別のポートフォリオが取り得るリスク・リターン( $n=2$ )
(左図：ロングのみ( $0\leq\omega_i\leq1$ )、右図：ショートを許容( $-1\leq\omega_i\leq1$ ) )

　図表5(特に左図)から分かるとおり、相関が小さくなると(特に $\rho=-1$ のとき)、同じ期待リターン水準(特に $\mu_P=0.03$ 近辺)でもリスクが大きく相違していることが分かる。

3.2.2.　ナイーブ・ポートフォリオ

　各証券に等比率 $\displaystyle{\frac{1}{n}}$ で投資したポートフォリオをナイーブ・ポートフォリオと呼ぶ。証券 $i,j$ のリターンの共分散 $\sigma_{ij}$ を

$\begin{aligned} \sigma_{ij}=&\begin{cases} \sigma^2&,i=j,\\ \alpha\sigma^2,\ 0\lt\alpha\lt1&,i\neq j \end{cases} \end{aligned}$

と仮定すれば、このナイーブ・ポートフォリオのリターン $r_{P_n}$ について

$\begin{aligned} E[r_{P_n}]=&\displaystyle{\frac{1}{n}\sum_{i}^{n}E[r_i}],\\ V[r_{P_n}]=&\displaystyle{\frac{1}{n^2}\sum_{i=1}^{n}\sigma^2}+\displaystyle{\sum_{i\neq j}{\sigma_{ij}}^2}\\ =&\displaystyle{\frac{\sigma^2}{n}}+\alpha\sigma^2\displaystyle{\frac{n(n-1)}{n}}=\sigma^2\left(\alpha+\displaystyle{\frac{1-\alpha}{n}}\right) \end{aligned}$

が成り立つ。このリスクについて

$\begin{aligned} V[r_{P_n}]=\sigma^2\left(\alpha+\displaystyle{\frac{1-\alpha}{n}}\right)\rightarrow\alpha\sigma^2,\ (n\rightarrow\infty) \end{aligned}$

が成り立つ。
　ナイーブ・ポートフォリオの分散はこのように少ないパラメータ( $\alpha, \sigma$ )で記述できる。ポートフォリオのリターンを多変量分布に従う乱数として生成してシミュレーションする際に、パラメータの評価が便利であることから、ナイーブ・ポートフォリオは理論的な考察において度々用いられる*5。