長期投資の理論と実践（05/X） - 「大人の教養・知識・気付き」を伸ばすブログ

　投資理論を以下の書籍

長期投資の理論と実践: パーソナル・ファイナンスと資産運用

作者:安達智彦,池田昌幸
東京大学出版会

Amazon

をベースに学ぶこととする。

前回

power-of-awareness.com

前回
4.　平均・分散分析とCAPM
- 4.1　平均・分散分析
今回のまとめ
次回

4.　平均・分散分析とCAPM

　効用関数とリターンの従う確率分布に制約を加えるならば、期待効用を高めるポートフォリオはリターンの期待値と分散のみによって決定できる。

4.1　平均・分散分析

　投資家がリターンに関して期待リターンおよび分散(またはリスク)のみに興味を持ち、同じ分散ならばより大きな期待リターンを、同じ期待リターンならばより小さい分散を選好するとき、投資家は平均・分散選好という。投資家のリスク・リターンに対する姿勢が平均・分散選好で表されるならば、効用関数の情報を明示的に扱う必要がなくなる。また平均・分散選好をもつ投資家であれば、リターンが正規分布に従うか否かにかかわらず、確率分布の期待値と分散の関係のみでポートフォリオを議論できる。こうしたポートフォリオの分析方法を平均・分散分析*1という。

4.1.2　効率的ポートフォリオと2基金分離

　ここでは任意の効率的ポートフォリオが2つの最小分散ポートフォリオ(以降、それらのウェイト $\boldsymbol{\omega}_Q,\boldsymbol{\omega}_G$ で表す。)を合成することで構築できることを確認する。
　まず前回導出した期待リターン $\mu_P$

$\begin{aligned} \mu_P^{*}=\displaystyle{\frac{\sqrt{(C\sigma_P^2-1)(BC-A^2)}}{C}+\frac{A}{C}} \end{aligned}$

を $\sigma-\mu$ 平面にプロットすると以下のようになる。

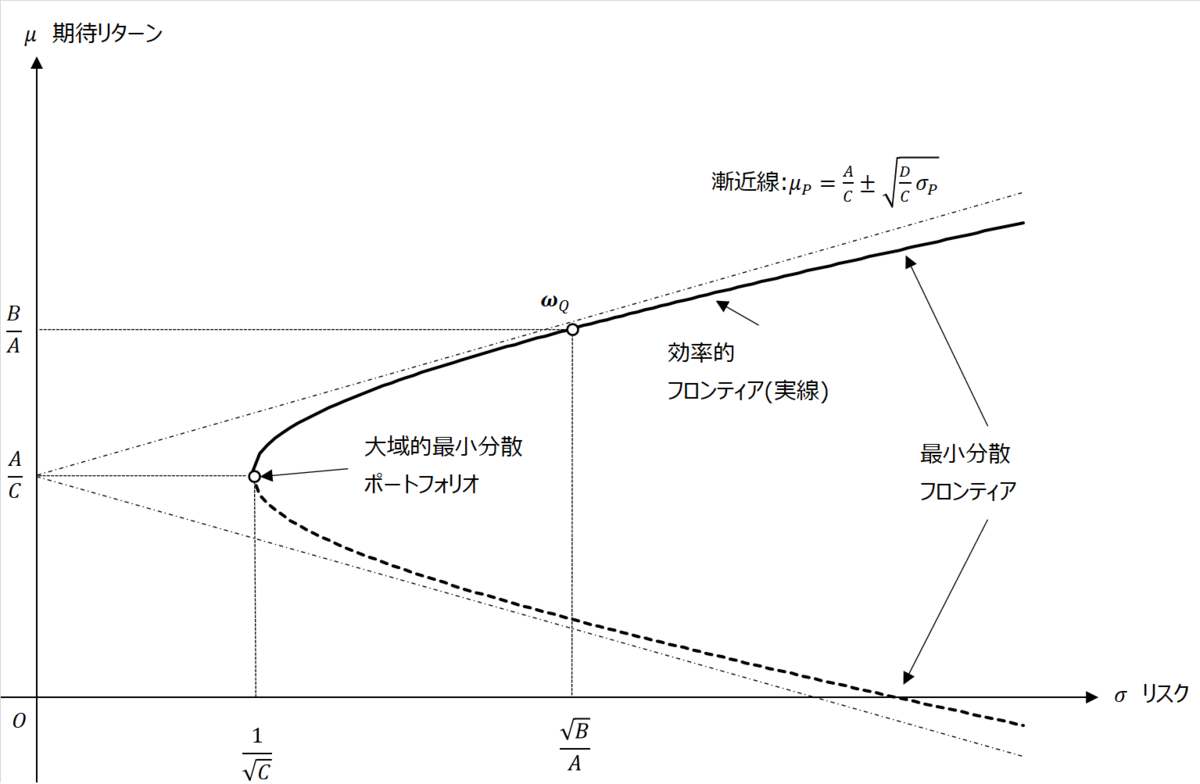
この曲線は頂点が $\left(\displaystyle{\frac{1}{\sqrt{C}}},\displaystyle{\frac{A}{C}}\right)$ で、漸近線が $\mu_P=\displaystyle{\frac{A}{C}}\pm\sqrt{\displaystyle{\frac{D}{C}}}\sigma_P$ であるような双曲線である。
　双曲線上に位置するポートフォリオは、期待リターンを所与としたときに最小のリスクを与えるため最小分散ポートフォリオと呼ぶ。最小分散ポートフォリオの中でも最小の分散を与える点を大域的最小分散ポートフォリオというのだった。

　さて $\boldsymbol{\omega}_Q=\displaystyle{\frac{\Omega^{-1}\boldsymbol{\mu}}{A}},\boldsymbol{\omega}_G=\displaystyle{\frac{\Omega^{-1}\boldsymbol{1}}{C}}$ とおくと、これらはそれぞれポートフォリオの投資ウェイトと解釈できる。これらの期待リターンおよびリスクは

$\begin{aligned} \mu_Q&={}^{t}\boldsymbol{\mu}\boldsymbol{\omega}_Q=\displaystyle{\frac{{}^{t}\boldsymbol{\mu}\Omega^{-1}\boldsymbol{\mu}}{A}}=\displaystyle{\frac{B}{A}},\\ \sigma_Q^2&={}^{t}\boldsymbol{\omega}_Q\Omega\boldsymbol{\omega}_Q=\displaystyle{\frac{B}{A^2}},\\ \mu_G&={}^{t}\boldsymbol{\mu}\boldsymbol{\omega}_G=\displaystyle{\frac{{}^{t}\boldsymbol{\mu}\Omega^{-1}\boldsymbol{1}}{C}}=\displaystyle{\frac{A}{C}},\\ \sigma_G^2&={}^{t}\boldsymbol{\omega}_Q\Omega\boldsymbol{\omega}_G=\displaystyle{\frac{1}{C}} \end{aligned}$

であり、

$\begin{aligned} \sigma_Q^2=\displaystyle{\frac{\mu_Q^2}{B}}&=\displaystyle{\frac{1}{B}\frac{1}{BC-A^2}\left(BC-A^2\right)\mu_Q^2 }\\ &=\displaystyle{\frac{1}{BC-A^2}\left(C-\frac{A^2}{B}\right)\mu_Q^2 }\\ &=\displaystyle{\frac{1}{BC-A^2}\left(C\mu_Q^2-\frac{A^2}{B}\frac{B^2}{A^2}\right) }\\ &=\displaystyle{\frac{1}{BC-A^2}\left(C\mu_Q^2-\frac{1}{B}\right) }\\ &=\displaystyle{\frac{1}{BC-A^2}\left(C\mu_Q^2-2A\mu_Q+B\right)},\\ \sigma_G^2=\displaystyle{\frac{\mu_G}{A}}&=\displaystyle{\frac{1}{BC-A^2}\frac{(BC-A^2)\mu_G}{A}}\\ &=\displaystyle{\frac{1}{BC-A^2}\left(\frac{BC}{A}-A\right)\mu_G}\\ &=\displaystyle{\frac{1}{BC-A^2}\left(B-A\mu_G\right)}\\ &=\displaystyle{\frac{1}{BC-A^2}\left(B-A\mu_G+C\mu_G^2-A\mu_G\right)}\left(\because C\mu_G^2-A\mu_G=\displaystyle{\frac{A^2}{C}}-\displaystyle{\frac{A^2}{C}}=0\right)\\ &=\displaystyle{\frac{1}{BC-A^2}\left(C\mu_G^2-2A\mu_G+B\right)} \end{aligned}$

といずれも最小分散フロンティア上の点である、すなわち最小分散ポートフォリオであることが分かる。
　これらを用いると、

$\begin{aligned} \boldsymbol{\omega}^{*}&=\sqrt{\displaystyle{\frac{C\sigma_P^2-1}{D}}}\Omega^{-1}\boldsymbol{\mu}+\displaystyle{\frac{1}{C}}\left(1-A\sqrt{\displaystyle{\frac{C\sigma_P^2-1}{D} }}\right)\Omega^{-1}\boldsymbol{1}\\ &=A\sqrt{\displaystyle{\frac{C\sigma_P^2-1}{D}}}\boldsymbol{\omega}_Q+\left(1-A\sqrt{\displaystyle{\frac{C\sigma_P^2-1}{D} }}\right)\boldsymbol{\omega}_G\\ \end{aligned}$

を得る。 $A\sqrt{\displaystyle{\frac{C\sigma_P^2-1}{D}}}+\left(1-A\sqrt{\displaystyle{\frac{C\sigma_P^2-1}{D} }}\right)=1$ であるから、これは効率的ポートフォリオ $\boldsymbol{\omega}^{*}$ が2つのポートフォリオ $\boldsymbol{\omega}_Q,\boldsymbol{\omega}_G$ の線形結合で表されることを意味する。この性質を2基金分離(Two fund separation)という。

4.1.3　無差別曲線と期待効用最大化問題

　平均・分散選好のもとでの最適ポートフォリオの決定問題を投資機会集合と無差別曲線を用いて考える。無差別曲線は投資リターンの確率分布と効用関数の具体的な関数形を特定しなければならないため、ここではリターンが正規分布、効用関数が

$\begin{aligned} u(x)=-e^{-\phi x},\ \phi\gt0 \end{aligned}$

だと仮定する。ここで $\displaystyle{-\frac{u^{\prime\prime}(x)}{u^{\prime}(x)}}=\phi$ であるあｋら、 $\phi$ は絶対的リスク回避度を表す。
　いま期初の投資可能額 $W_{0}$ を単利ネット表示で $r_P$ の投資リターンを表すポートフォリオで1期間運用するものとする。 $r_P\sim N(\mu_P,\sigma_P^2)$ とすれば、

$\begin{aligned} E[u(\tilde{W})]=-\exp\left\{-\phi\left(W_0(1+\mu_P)-\displaystyle{\frac{\phi}{2}}\sigma_W^2\right)\right\} \end{aligned}$

である。確実性等価の定義式から、

$\begin{aligned} &E[-e^{-\phi\tilde{W}}]=-\exp\left\{-\phi\left(W_0(1+\mu_P)-\displaystyle{\frac{\phi}{2}}\sigma_W^2\right)\right\}=-\exp\left(-\phi W^{\mathrm{CE}}\right)\\ \Leftrightarrow&W^{\mathrm{CE}}=W_0(1+\mu_P)-\displaystyle{\frac{\phi}{2}W_0^2\sigma_P^2} \end{aligned}$

を得る。ここからリスクプレミアムが $\displaystyle{\frac{\phi}{2}W_0^2\sigma_P^2}$ だと分かる。
　この富を実現するような投資リターンは

$\begin{aligned} \displaystyle{\frac{W^{\mathrm{CE}}}{W_0}}-1=\mu_P-\displaystyle{\frac{\phi}{2}W_0\sigma_P^2} \end{aligned}$

で与えられる。これを確実性等価リターンという。
　さて無差別曲線は $(\sigma,\mu)$ 平面において、同一の期待効用をもたらす $(\sigma_P,\mu_P)$ の軌跡であった。したがって $(\sigma_P,\mu_P)$ を用いて期待効用を書き直すと

$\begin{aligned} E[u(\tilde{W})]=-\exp\left\{-\phi\left(W_0(1+\mu_P)-\displaystyle{\frac{\phi}{2}W_0^2\sigma_P^2}\right)\right\} \end{aligned}$

であった。これを $k$ とおけば、 $k$ が大きいほどより大きい期待効用を表すことになる。
　さてこれを $\mu_P$ に関して表せば無差別曲線を得られることから、

$\begin{aligned} \mu_P=\displaystyle{\frac{\phi}{2}W_0\sigma_P^2}-1-\frac{1}{\phi W_0}\log(-k) \end{aligned}$

とリスクに関する二次関数として表されることが分かる。
　無差別曲線は実際に実現できるかを無視した、すなわち投資機会集合の存在を無視した概念であるから、さきほどの効率的フロンティアとの交点を考える必要がある。
　 $\phi$ は絶対的リスク回避度であったから、 $\gamma=\phi W_0$ は相対定期リスク回避度と解釈できる。また $K=-1-\displaystyle{\frac{1}{\phi W_0}\log(-k)}$ とおけば

$\begin{aligned} \mu_P=\displaystyle{\frac{\phi}{2}W_0\sigma_P^2}+K \end{aligned}$

を得る。 $K$ が $k$ の単調増加関数であるから、 $K$ が大きいほどより大きい期待効用を表す。また $y=\log(x)$ は全単射であることも踏まえれば、 $K$ を期待効用水準と読み替えて良いことが分かる。このとき

$\begin{aligned} K=-1-\displaystyle{\frac{1}{\phi W_0}\log(-k)}=\mu_P-\displaystyle{\frac{\phi}{2}W_0\sigma_P^2 }=\mu_P-\displaystyle{\frac{\gamma}{2}\sigma_P^2} \end{aligned}$

であり、確実性等価リターンに一致することに注意する。
　さて本筋に戻り $K$ の値に応じて無差別曲線と効率的フロンティアの交点を考えると、

$\begin{aligned} \begin{cases} \left(C\mu_P^{*}-A\right)^2&=(C{\sigma_P^{*}}^2-1)(BC-A^2)\\ \mu_P^{*}&=\displaystyle{\frac{\gamma}{2}{\sigma_P^{*}}^2}+K \end{cases} \end{aligned}$

を解けばよい。これを解くことで

$\begin{aligned} (\sigma_P^{*},\mu_P^{*})=\left(\displaystyle{\frac{1}{\sqrt{C}}\sqrt{1+\displaystyle{\frac{D}{\gamma^2}} }}, \displaystyle{\frac{A}{C}}+\displaystyle{\frac{D}{\gamma C}}\right) \end{aligned}$

を得る。

　 $C,D$ はいずれも正値であるから、 $\gamma$ の値が小さいほど最適ポートフォリオの期待リターンおよびリスクはいずれも大きくなり、「ハイリスク・ハイリターン」を意味する。逆に極端にリスク回避的な投資家として、 $\gamma\rightarrow\infty$ とすれば、

$\begin{aligned} (\sigma_P^{*},\mu_P^{*})\rightarrow\left(\displaystyle{\frac{1}{\sqrt{C}}}, \displaystyle{\frac{A}{C}}\right) \end{aligned}$

が得られ、これは大域的最小分散ポートフォリオに他ならない。

4.1.3　最適ポートフォリオと2基金分離

　前節で示したとおり、任意の効率的ポートフォリオは2つの最小分散ポートフォリオによって合成でき、

$\begin{aligned} \boldsymbol{\omega}^{*}=A\sqrt{\displaystyle{\frac{C{\sigma_P}^2-1}{D}}}\boldsymbol{\omega}_Q+\left(1-A\sqrt{\displaystyle{\frac{C{\sigma_P}^2-1}{D}}}\right)\boldsymbol{\omega}_G \end{aligned}$

と表現できる。
　同じように、投資家の期待効用最大化を明示的に考慮した、最適ポートフォリオのリスク・期待リターンは

と表された。この結果を代入すれば、

$\begin{aligned} \boldsymbol{\omega}^{*}&=A\sqrt{\displaystyle{\frac{1}{D}\left\{C\left(\frac{1+\frac{D}{\gamma^2}}{C}\right)-1\right\}}}\boldsymbol{\omega}_Q+\left(1-A\sqrt{\displaystyle{\frac{1}{D}}\left\{C\left(\displaystyle{\frac{1+\frac{D}{\gamma^2}}{C}}\right)-1\right\}}\right)\boldsymbol{\omega}_G\\ &=\displaystyle{\frac{A}{\gamma}}\boldsymbol{\omega}_Q+\left(1-\displaystyle{\frac{A}{\gamma}}\right)\boldsymbol{\omega}_G \end{aligned}$

を得る。このように相対的リスク回避度を用いて2基金分離を表現できる。
　これは指数型効用関数をもつ投資家が選択する最適ポートフォリオは $\boldsymbol{\omega}_Q,\boldsymbol{\omega}_G$ という2つの最小分散ポートフォリオに

$\begin{aligned} \displaystyle{\frac{A}{\gamma}}:1-\displaystyle{\frac{A}{\gamma}} \end{aligned}$

の比率で投資配分して合成できることを意味する。さらに、通常の資産市場では $A={}^{t}\boldsymbol{\mu}\Omega^{-1}\boldsymbol{1}\gt0$ であるから、リスク回避度が大きいほど、よりハイリスク・ハイリターンであるようなポートフォリオ $\boldsymbol{\omega}_Q$ への投資を控え、リスクが小さい方の $\boldsymbol{\omega}_G$ への投資を増やすべきことを意味する。