マクロ経済学（3/17）企業の設備投資行動 - 「大人の教養・知識・気付き」を伸ばすブログ

　基本的な経済観念を身に付けるべく、マクロ経済学を学んでいく。テキストは古典派をしっかりと扱っているという

マクロ経済学第2版

作者:二神孝一,堀敬一
有斐閣

Amazon

を用いることにする。

3. 企業の設備投資行動

3.1 マクロ経済における投資の役割

　投資とは、将来のリターンを期待して資金や労力を現時点で投入すること。マクロ経済学では主に総固定資本形成と在庫変動、研究開発費に限定される。
　したがって

$\begin{aligned} 総固定資本形成=公的固定資本形成+民間企業設備投資+民間住宅投資 \end{aligned}$

である。ここで、

(1)公的固定資本形成	：いわゆる公共工事
(2)民間企業設備投資	：いわゆる設備投資
(3)民間住宅投資	：家計による住宅の購入

また、 $在庫投資=生産量-販売量$ である。他方で、研究開発投資は企業が行う投資の1つとして無視できない規模を占める。

3.1.1 設備投資の二面性

　GDPと設備投資について、設備投資はGDPにて消費に次いで2番目に大きな比率を占める。また現在の設備投資は資本ストックとして将来の生産に貢献する。資本ストックとはある時点で企業が保有する機械や建物などの総量を指す。

$\begin{aligned} I_t=K_{t+1}-K_t+\delta K_t \end{aligned}$

ここで、

$I_t$	：時点tにおける設備投資額
$K_t$	：時点tにおける資本ストック
$\delta$	：固定資産減耗

である。

3.2 新古典派投資理論

　企業において設備投資の意思決定を検討してみる。
　生産関数を $F$ として時点 $1$ の利益 $\pi_1$ は、

$\begin{aligned} \pi_1=F(K_1)-I_1 \end{aligned}$

で表される。
　「資本の限界生産性が正であるものの資本ストックの増加に伴い漸減する」と仮定すると、第 $2$ 期の生産量は

$\begin{aligned} K_2=I_1+(1-\delta) K_1 \end{aligned}$

が成り立つから、

$\begin{aligned} \pi_2=F(K_2)+(1-\delta)K_2 \end{aligned}$

である。以上からこの企業が直面する問題は、企業価値

$\begin{aligned} V(I_1 )=\pi_1+\displaystyle{\frac{1}{1+r}},\ \ \pi_2=F(K_1 )-I_1+\displaystyle{\frac{F(K_2 )+(1-\delta)K_2}{1+r}} \end{aligned}$

を最大化するように $I_1$ を決定する問題である。ただしrは割引率である。
　このとき最適な資本ストック $K_2^*$ は

$\begin{aligned} V^{\prime}(I_1)=0\Leftrightarrow -1+\displaystyle{\frac{F^{\prime}(K_2^{*})+(1-\delta)}{1+r}}=0\Leftrightarrow F^{\prime}(K_2^*)=r+\delta \end{aligned}$

を満たす。
　 $K_1$ は所与であり企業に決定権は無いため、 $K_1$ を所与として $K_2^*$ になるまで資本ストックを変化させることになる。これは資本の使用者費用という概念で説明可能である。
　資本の使用者費用とは「資本ストックを1単位使用する際に必要な費用」を指す。

図表1　最適な資本ストック水準の決定

出典：二神・堀(2017)*1

　企業が資金を借り入れることによって資本財を購入した場合、毎期支払う利息金利が「利子の費用」である。企業が充分な資金を保有しているとしても資本ストックを購入すると、その余剰資金を金融資産に投資することで得られたはずの利息を失うことになる。これを機会費用という。
　生産設備の老朽化に伴う費用を「資本減耗の費用」という。企業価値が最大なのは、 $限界生産性=利子費用+資本減耗費用$ のときである。すなわち追加的な生産量と追加的な費用が一致することを意味する：

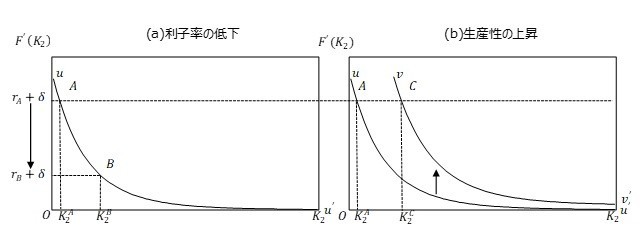
$\begin{aligned} F^{\prime} (K_2^*)=r+\delta \end{aligned}$

　図表1において、曲線 $uu^{\prime}$ は資本の限界生産性および資本の使用者費用との関係を表す。ここでは資本の限界生産性が逓減するため、下に凸である。この図表では、

利子率が低下（ $r_A+\delta\rightarrow r_B+\delta$ ）すれば最適な資本ストックは $K_2^A\rightarrow K_2^B$ と増大する。
企業の生産技術に技術革新による正の生産性ショック（ $uu^{\prime}\rightarrow vv^{\prime}$ ）が生じた場合、最適な資本ストックは $K_2^A\rightarrow K_2^C$ と増大する。

　これらの場合、資本ストックが変化したことでそれに対応した設備投資が行われる：

$\begin{aligned} I_t^*=K_{t+1}^*-K_t+\delta K_t \end{aligned}$

以上のようなモデルを新古典派投資理論という。このとき

$\begin{aligned} I_1=I(r),I^{\prime}(r)\gt0 \end{aligned}$

が成り立つ。

3.3 調整費用モデル

　新古典派理論には問題がある。それは「将来への期待が設備投資に与える影響が考慮されていない点」である。2期間以上の長期的な設備投資計画を検討しているとする。将来の利子率が徐々に上昇することを既知とすれば、ここまでの議論を踏まえるならば、将来の望ましい資本ストック水準は徐々に低下するはずである。そうであれば、現在の資本の限界生産性と使用者費用が示唆する最適な資本ストック水準よりも、より少ない水準を目標として設備投資は決定される。
　これに対して、新古典派投資理論は今日の設備投資を決定するのに将来の利子率上昇を考慮する必要はないと主張する。なぜならば将来に利子率が上昇するならば、その時点で最適な資本ストック水準が実現するように設備投資を決定すればよいからだ。その背景には各期の最適な資本ストック水準に企業が速やかに調整可能であることを前提視していることがある。
　こうした将来期待が設備投資に与える影響に関する問題点を克服した理論として「調整費用モデル」がある。現在および将来の資本の限界生産性や使用者費用を考慮して現在の設備投資を決定する。
　ある企業が図表2に示される2つの計画のうち一方を実行することを検討しているとする。ここで $I^A=\displaystyle{\frac{I^B}{2}}$ という関係を仮定する。するといずれの投資計画であっても最終的に投入する投資額は一致する。しかし調整費用の関数形が相違し平均費用は計画2の方が小さい。したがって計画2を選択することが合理的である。

図表2　ある企業が検討している設備投資計画

	第 $1$ 期の投資	第 $2$ 期の投資	調整費用
計画1	$0$	$I^B$	$C(I^B )$
計画2	$I^A$	$I^A$	$2C(I^A )$

3.4 その他の投資

　在庫投資は生産量が販売量を上回れば正になる一方で下回れば負になる。通常企業は在庫増を好まないものの、実際には在庫投資を行なう場合がまま多い。これを説明するのが生産平準化理論である。需要の変動に拘わらずに各期で生産量を一定に保つために在庫投資を行なうという理論である。
　他方で、研究開発投資では、研究開発という不確実なものが適正になされるためには、特許や著作権で権利が保護される必要がある。

補論：平均 $q$ と限界 $q$

　新古典派理論の問題点を別の方法で克服した理論としてTorbinの $q$ 理論がある。
　企業の目的を、株式ですべて資金を調達しているとして、配当の割引現在価値の合計、すなわち株価の最大化と理解する。その上で、

$\begin{aligned} 平均q=\displaystyle{\frac{株価総額+負債総額}{資本の再取得費用}} \end{aligned}$

を定義する。これには

$\begin{aligned} 平均q\geq1\Rightarrow非負の設備投資平均q\lt1\Rightarrow負の設備投資 \end{aligned}$

を行なうという関係性があると考える。また

$\begin{aligned} 限界q=\displaystyle{\frac{資本を1単位増大させた場合の企業価値の増加分}{資本を1単位増大させた場合の資本の再取得価格}} \end{aligned}$

を定義し、

$\begin{aligned} 限界q\geq1\Rightarrow 設備投資を増大させる限界q\lt1\Rightarrow 設備投資を減少させる \end{aligned}$

とも考える。

次回

power-of-awareness.com

問題*2

1. 最適な粗投資額

　ある企業が資本のみを用いて生産を行なっている。その企業の生産関数は $F(K_t )=K_t^0.5$ で表されると仮定する。

(a)最適な粗投資額①

　利子率 $r=3\%$ , 資本減耗率 $\delta=2\%,K_t=50$ である場合、最適な粗投資額はいくらか。

(b)最適な粗投資額②

　利子率がある値になったとき、最適な粗投資額が $351$ になった。利子率以外は(a)と同一の値であるするとき、利子率はいくらか。

2. 利益の関係

　企業の生産関数を $Y=\sqrt{K}$ とする。資本減耗率 $\delta=1$ とする。このとき第1期の利益 $\pi_1$ および第2期の利益 $\pi_2$ の関係を図示せよ。

3.2期間設備投資問題

　ある企業の2期間の設備投資問題を考える。この企業の生産可能性曲線が $(\pi_1 )^2+(\pi_2 )^2=22,100$ である。なお $\pi_1$ および $\pi_2$ はそれぞれ第1期と第2期に支払われる利益とする。資本減耗率 $\delta=0$ および利子率 $r=10\%$ を仮定するとき、以下の問いに答えよ。

(a)企業価値の最大化

　企業価値を最大にするような $(\pi_1,\pi_2)$ を求めよ。

(b)最適資本ストック

　第2期の最適な資本ストック $K_2$ を求めよ。

4.新古典派理論に則り以下の問いに答えよ。

(a) 第1期の売上高 $F(K_1)$ のみに対してある税率で課税されることになった。このことが企業の設備投資にどのような影響を与えるか答えよ。
(b) 第2期の売上高 $F(K_2)$ のみに対してある税率で課税されることになった。このことが企業の設備投資にどのような影響を与えるか答えよ。