基本的な経済観念を身に付けるべく、マクロ経済学を学んでいく。テキストは古典派をしっかりと扱っているという
を用いることにする。
前回
2. 家計の消費・貯蓄行動
2.2 家計はどのように消費を決定するのか
- 家計における消費と貯蓄の振り分け目的:消費すれば現在の効用が上昇するから。貯蓄は将来の消費のため。家計は現在と将来の消費から得られる効用、現在や将来の所得を考えて現在の消費と貯蓄を決定する
- 2期間モデルによる分析:家計が2期間の効用を最大にするように現在と将来の消費を決定する。このときの家計の効用関数を以下で表す。ここで
は第
期の消費であり、
を主観的割引率という。
により同じ量を消費したとしても得られる効用が相違し得ることを表現している。
- また
すなわち限界効用は正かつそれは逓減すると仮定する。
- 予算制約を考慮すると
- 第1期の予算制約:家計が
の所得を得るとし、
を消費し
ならば
が貯蓄される。その
は利子率
で運用され、第2期には
の所得を発生させる。逆に
ならば
の借入を行ない、第2期には
の元利金を返済する
- 第2期の予算制約:家計が
の所得を得るとすると、この時点ではさらに貯蓄分(または返済分)を考慮する。この家計が遺産を残さないことを仮定すれば、第2期の予算制約は
- 最右辺の
を生涯所得という
- 上記の家計における最適な消費計画は、制約条件
- 制約条件から
を代入することで
これを最大化するようなは
を満たすので
これをEuler方程式という。
- Euler方程式は一般に代数的に解くことができない。特殊条件下での代数解を導出する:
仮定
を追加すると、
であるからEuler方程式は
当初求めた式に代入することで
ならばEuler方程式が
となるため、
である。したがって
ここで
である
- 以上を要約すれば
- 現在と将来の消費は平準化されている
- 現在(将来)の消費は現在の所得のみならず将来の所得も考慮して決定される
2.3 貯蓄関数
- 消費、貯蓄を決定する要因:(1)所得、(2)主観的割引率、(3)利子率
- 将来所得が一定で現在の所得だけが変化する場合、家計は消費の平準化を行なっているため、
が増加したとしても、
も増えるためその増加ほど
は増加しないため、現在の所得の増加は貯蓄を増加させる
- 現在の所得が一定で将来所得だけが変化する場合、
の増加は
の増加をもたらすため、将来所得の増加は貯蓄を減少させる。利子率が上昇した場合には、Euler方程式
から消費成長率()が上昇する。
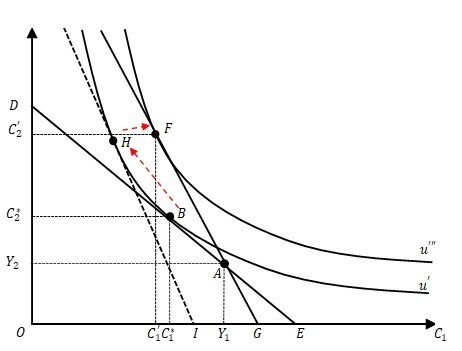
- 利子率が
のとき、ある家計の2期間の所得
が点
で与えられているとする。予算制約線
であり、この家計の無差別曲線が
であるとすれば、点
が最適消費計画となる。
- 利子率が
に上昇した場合の最適な消費計画を考える。このとき、予算制約線は直線
に変わる。消費は利子率の影響を受けないため、点
を通ることは変わらない。最適消費計画は点
となる
- 以上から、点
から点
への変化は、2つの効果に分けることが出来、それらの効果の大きさで貯蓄の増減が決まる
- 代替効果:点
→点
利子率が上昇すれば予算制約線の傾き(=
)が増加する、すなわち将来の価格が相対的に減少する。その結果、第
期の消費財への需要を減らし代わりに第
期の消費財への需要を増やす。
- 所得効果:点
→点
家計は
が
を上回っているため正の貯蓄を行なっている。利子率が上昇するため、第
期に受け取る利子収入が増大する。したがって家計の所得全体が増加することで
が増加する。
- すなわち
- 時間選好率:主観的割引率
は時間選好率と密接に関係している。消費量が同じでも第
期に比べ第
期の効用を相対的に小さく評価する:
を仮定すると、利子率
は第
期の消費を
単位減らすことで可能となる第2期の追加的な消費量を表す。時間選好率
は家計が第
期の消費を
単位減らしたときに減少する効用を維持するだけの第
期の追加的な消費量を表す。このため、
となる組み合わせを最適消費計画として家計は選択する。ここで
が上昇したと仮定すると、
は下落する。
2.4 消費に関するいくつかのモデル
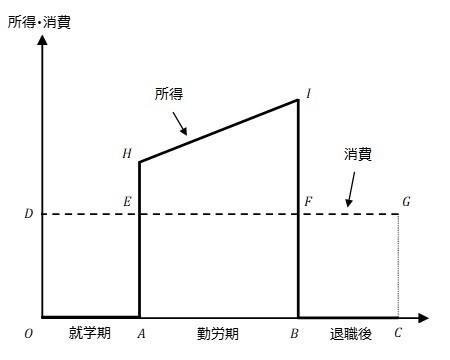
- ライフサイクル仮説:現在から死亡するまでのことを考えて消費計画を立てるという仮説
- 家計は現時点から死ぬまでに得る生涯所得を予測して一生の消費計画を立てる:①各期の消費は生涯を通して一定であると仮定する、②就学期から若年勤労期は借金をして消費する。退職後は貯蓄を崩して消費する
期の消費
と恒常所得は
- 可処分所得が
から
と増大すると、平均消費性向は(
の傾きから
の傾きへと)減少する
補論1:最適な消費計画の決定
- 複数の財に対する選好は限界代替率で表現する。限界代替率は一方の財で測ったもう一方の財の価値を表し
と書く。
- 限界代替率の考え方を用いれば、消費者がどのように最適な消費計画を決定しているのかを理解することができる。消費者の利用可能な所得を
, 第
財の価格を
, 第
財の価格を
で表すこととする。このとき予算制約式は
補論2:双曲割引
合理的に行動しているとは考えられない家計の行動を分析するためのツールとして双曲割引がある。
家計の消費の計画期間を3期間とする。このとき
と効用関数が書ける。簡単のために所得は第1期のみが発生しまた
であると仮定する。このとき
問題*4
1. 問題
をそれぞれ第1期および第2期の消費として、効用関数
をもつ家計の消費と貯蓄の選択問題を考える。このとき以下の問いに答えよ。ただしこの家計の予算制約式を
とする。ここでを利息、
を
期の所得とする。
- (a)生涯所得
の場合、この家計の生涯所得を計算せよ。
- (b)最適消費計画①
前問において更にと仮定する。この場合の最適な消費計画
および貯蓄額を計算せよ。
- (c)最適消費計画②
前問においてへと変化した場合、最適な消費計画
を計算せよ。
- (d)最適消費計画③利子率が変化した場合
(b)においてへと変化した場合、最適な消費計画
を計算せよ。
2. 問題
をそれぞれ第
期および第
期の消費として、効用関数
をもつ家計の消費と貯蓄の選択問題を考える。このとき以下の問いに答えよ。ただしこの家計の予算制約式を
とする。ここでを利息、
を
期の所得とする。
- (a)問題
の場合、最適な消費計画
および貯蓄額を計算せよ。
- (b)問題
前問と同様の状況だがへと変化した場合の最適な消費計画
を計算せよ。
3. 問題
ある家計の効用関数が
で表されるとする。そのとき以下に答えよ。
- (a)問題
この家計の時間選好率を計算せよ。
- (b)問題
が上昇したときに時間選好率はどのように変化するか。またその理由を説明せよ。
- (c)問題
この家計が直面する予算制約式が
とする。ここでを利息、
を
期の所得とする。また
であると仮定する。このときに最適な消費計画
と貯蓄額(あるいは借入額)を求めよ。
4.家計の効用
について、と仮定する。このとき以下の2つの命題が成り立つことを示せ:
- (a)問題
現在の所得が増加するものの将来所得が一定であるならば、貯蓄は増加する。
- (b)問題
現在の所得が一定であるものの将来所得が増加するならば、貯蓄は減少する。
5. 家計の効用
解答
1. 家計の消費決定(1)
- (a) 生涯所得
定義より生涯所得は
- (b) 最適消費計画①
であるとき、Euler方程式より
が成り立つ。(a)および予算制約からであるから
これをに代入して
である。このとき
である。
- (c) 最適消費計画②
(b)と同様に考え、
が成り立つ。(a)および予算制約式から
であるから、
を得る。このとき
である。
- (d) 最適消費計画③利子率が変化した場合
になった場合、(b)と同様に考え、
が成り立つ。(a)および予算制約式から
であるから、
を得る。このとき
である。
2. 家計の消費決定(2)
問題設定を整理すると、
である。
- (a)最適消費計画
まず
である。また予算制約式よりである。したがって
またである。
貯蓄額は
である。
- (b)
の場合
このとき、であるからEulerの公式より
が成り立つため、
である。
3. 家計の選好
- (a)時間選好率の計算
定義より
- (b) 時間選好率の変化の仕方
時間選好率をに関して微分すると
と任意のに対して正であるから、
が増加すると時間選好率は増加する。
- (c) 最適消費計画
このときEulerの方程式より
であるから、が成り立つ。
予算制約式よりであるから、
である。また、すなわち
だけ借入れている。
4. 貯蓄と所得の関係
のとき、Eulerの方程式より
が成り立ち、予算制約式より
したがって貯蓄について
が成り立ち、将来所得が一定のもとで現在の所得が増大すれば貯蓄は増大し、現在の所得が一定で将来所得が増大すれば貯蓄は減退する。
5. 限界消費性向
4.と同様にして
が成り立つ。
短期では、長期では
になるとすれば、
- 短期限界消費性向:
- 長期限界消費性向:
となる。