「大人の教養・知識・気付き」を伸ばすブログ

一流の大人（ビジネスマン、政治家、リーダー…）として知っておきたい、教養・社会動向を意外なところから取り上げ学ぶことで“気付く力”を伸ばすブログです。データ分析・語学に力点を置いています。　→現在、コンサルタントの雛になるべく、少しずつ勉強中です(※2024年1月21日改訂)。

MENU

マクロ経済学（9/17）経済成長の理論II：内生的成長モデル

経済学

　基本的な経済観念を身に付けるべく、マクロ経済学を学んでいく。テキストは古典派をしっかりと扱っているという

マクロ経済学 第2版

マクロ経済学 第2版

Amazon

を用いることにする。

前回

power-of-awareness.com

9. 　経済成長の理論II：内生的成長モデル

9.1.　新しい経済成長理論の登場

　ソロー・モデルの問題点である
　　①GDP成長率を決定する技術進歩率が外生的に決められていた、
　　②経済政策が経済成長に関与する余地が無い
を解決すべく、新しい経済成長理論が考案されてきた。
　新しい経済成長理論では、企業の生産性や技術は内生的に決定されると考える。こうした理論を内生的成長理論という。これらは2つのグループに分類できる。

  • 経済成長に関して資本の蓄積よりも技術革新が重視されていて、経済成長の鍵は企業の研究開発だと考える。企業の行動を利潤最大化行動に基づいて記述する。
  • 資本が経済成長において果たす役割を依然として重視し、資本の限界生産性が逓減しない仕組みを反映させる。

9.2　研究開発と経済成長のモデル

　研究開発投資に期待される成果は、これまでなかったものが新たに製品化され財の種類が増えることで、またその品質が改善されることである。
　しかし投資の成果は模倣が容易な場合があり、一方で、完全競争市場では超過利潤が発生しないために研究開発に対する対価が発生しない。そのため完全競争市場では研究開発を行なうインセンティブは存在せず、そのため政府は特許権や著作権を用いて企業や研究開発者の利益を保護する。

　特許権や著作権を導入した場合、市場は完全競争市場にはならなくなり、新技術やアイディアを研究開発者は独占的に行使できる。この独占市場では、企業は高めの価格を設定する一方で生産量は過少になる。こうした独占的に材を生産する企業が多数存在し自社が生産する財に対して価格支配力をもつ一方で、他の財を生産する企業と競争するような市場環境を独占的競争という。
　独占的競争を考慮した経済成長理論では、経済政策が大きな役割を果たす。特許権などによる研究開発者の権利保護は経済成長を促す一方で、生産者の独占は家計、ひいては経済全体の更生に負の影響を与える。したがってこれらのトレードオフを考慮して政府は政策を決定しなければならない

　以降、Grossman and Helpman(1991)のモデルを説明する。

9.2.1　質のはしごモデル

　家計がN種類の財を、それぞれの財を生産するN産業に属する企業から購入する。それぞれの産業は1企業から構成され、その独占企業は最先端の製品を生産し家計に販売している。これらの企業は家計部門から供給される労働を用いて生産を行なう。
　一方で、各企業は研究開発を、家計が供給する労働と資金により行なう。
　ある企業が研究開発に成功し、既存の独占企業が生産する財よりもより高品質の財を生産できることになったと仮定する。このとき研究開発に成功した企業は、既存企業に替わり新しい独占企業としてこの産業で生産活動を行う。こうしたモデルを「質のはしごモデル」という。

9.2.2　家計の選好と企業の価格競争

　研究開発に成功して新製品を生産できる企業と旧製品を生産する既存独占企業による競争を考える。
　ある1つの産業に着目する。この産業では両企業が提供する合計2つの製品が存在する。新製品を旧製品の\lambda倍だけ高く評価しており、このような質の違いを考慮して価格の安い方の財を購入すると仮定する。すなわち新製品価格をp_{\mathrm{new}}, 旧製品価格をp_{\mathrm{old}}とおけば、家計が以下のように財を選択するものとする：


\begin{aligned} p_{\mathrm{new}}\gt \lambda p_{\mathrm{old}}&\Longrightarrow旧製品を購入\\ p_{\mathrm{new}}\leq \lambda p_{\mathrm{old}}&\Longrightarrow新製品を購入 \end{aligned}


　また新製品か旧製品かにかかわらず財の生産には労働投入のみが必要で、企業は1単位の財の生産にa単位の労働投入が必要であるとする。すなわち各企業が新製品x_{\mathrm{new}}単位または旧製品x_{\mathrm{old}}単位を生産するには、それぞれa x_{\mathrm{new}},a x_{\mathrm{old}}だけ労働を投入する。このとき新製品を生産する企業の利潤\pi_{New}および旧製品を生産する企業の利潤\pi_{Old}は、賃金率をwとして、それぞれ


\begin{aligned} \pi_{New}&=(p_{\mathrm{new}}-wa)x_{\mathrm{new}},\\ \pi_{Old}&=(p_{\mathrm{old}}-wa)x_{\mathrm{old}} \end{aligned}


で与えられる。

　各企業の価格設定を考える。新製品を買ってもらうにはp_{\mathrm{new}}\leq \lambda p_{\mathrm{old}}を満たす必要があるため、これを満たす中でも最も高い価格であるp_{\mathrm{new}}=\lambda p_{\mathrm{old}}を選択する。したがって


\begin{aligned} \pi_{n}=(\lambda p_{\mathrm{old}}-wa)x_n \end{aligned}


が成り立つ。
　旧製品側はp_{\mathrm{new}}\gt \lambda p_{\mathrm{old}}を満たす範囲で値下げすることで新製品を生産する企業のシェアを奪うことができる。ただし新製品側が値下げすることでこれに対策することが出来る。
　旧製品側は利潤が発生するp_{\mathrm{old}}=waまでは価格を下げることが出来る。したがって新製品を生産する企業は


\begin{aligned} p_{\mathrm{new}}=\lambda p_{\mathrm{old}}=\lambda wa \end{aligned}


に設定することで旧製品を生産する企業を市場から駆逐できる。このときの利潤は


\begin{aligned} \pi_n=(p_{\mathrm{new}}-wa)x_{n}=wa(\lambda-1)x_n \end{aligned}


である。

　家計はN種類の財を消費して効用を得る。ここでは


\begin{aligned} u=\displaystyle{\sum_{i=1}^{n}\log{(q_i x_i)}}=\displaystyle{\sum_{i=1}^{n}\log{q_i}}+\displaystyle{\sum_{i=1}^{n}\log{x_i}} \end{aligned}


と効用関数を定義する。ここでx_iは第i財の消費量、q_iは第i財の質のレベルを表す。この式より、家計がN種類の財に対して支出する金額をEと所与であるとするとき、家計の予算制約式は


\begin{aligned} \displaystyle{\sum_{i=1}^{N} p_i x_i}=E \end{aligned}


と書ける。
　以上から、効用最大化条件を求めることができる。たとえば、第1財およびそれ以外の第j財の限界代替率MRS_{1,j}は2財の限界効用の比率に等しいから、


\begin{aligned} MRS_{1,j}=\displaystyle{\frac{\displaystyle{\frac{\partial u}{\partial x_1}}}{\displaystyle{\frac{\partial u}{\partial x_j}}}}=\displaystyle{\frac{x_j}{x_1}} \end{aligned}


が成り立つ。ここから

\begin{aligned} \displaystyle{\frac{x_j}{x_1}}=\displaystyle{\frac{p_1}{p_j}} \end{aligned}

が得られる。
　次に上記の


\begin{aligned} \displaystyle{\frac{x_j}{x_1}}=\displaystyle{\frac{p_1}{p_j}} \end{aligned}


を用いて各財に対する需要関数を導出する。これにより


\begin{aligned} x_j p_j=x_1 p_1,j=1,2\cdots,N \end{aligned}


が成り立つから、


\begin{aligned} \displaystyle{\sum_{j=1}^{N} p_j x_j}=E\Leftrightarrow Nx_1 p_1=E \end{aligned}


であり、ここから


\begin{aligned} x_1=\displaystyle{\frac{\displaystyle{\frac{E}{N}}}{p_1}} \end{aligned}


が得られる。これを導入することで


\begin{aligned} x_j=\displaystyle{\frac{\displaystyle{\frac{E}{N}}}{p_j}},\ j=1,2,\cdots,N \end{aligned}


であり、これら各財に対する需要関数を効用関数に代入することで


\begin{aligned} u=\displaystyle{\sum_{i=1}^{N} \log(q_i x_i)}=\displaystyle{\sum_{i=1}^{N} \log\left(q_i \frac{\displaystyle{\frac{E}{N}}}{p_i}\right)}=N\log{E}-N\log{N}+\displaystyle{\sum_{i=1}^{N} \log{\displaystyle{\frac{q_i}{p_i}}}} \end{aligned}


と変形できる。
　ここまでは1期間における問題であったが、多期間の場合を考える。この際に考慮すべきはEuler方程式である。この問題でのEuler方程式は


\begin{aligned} \displaystyle{\frac{E_t}{E_{t+1}}}=\displaystyle{\frac{1+\rho}{1+r}} \end{aligned}


で与えられる。

9.2.3.　研究開発

　研究開発について議論する。企業が研究開発の努力をI単位行うと確率Iで成功するものと仮定する。またすべての企業で同一の確率だとして、あるt期に投資すると同期間中にその成否が明らかになるものとする。さらに簡単化のために2つ以上の企業が研究開発に同時に成功することは無く、新製品をコピーすることは無いものとする。

成功確率：I
失敗確率：1-I


　研究開発に必要な労働はa_I単位だと仮定すれば、研究開発に必要な資金はwa_I Iである。

　この研究開発資金wa_I Iを株式発行により調達する場合、株価\hat{V}_tはどのように決定されるか。成功確率を踏まえ、


\begin{aligned} \hat{V}_t=IV_t+(1-I)\cdot0=IV_t \end{aligned}


で与えられる。他方で余計な資金が収益を一切生まないことから、制約条件として


\begin{aligned} V_t=wa_I \end{aligned}


が与えられる。
　独占企業であれば、他企業が研究開発に開発すると翌期には市場から退出しなければならない。その場合翌期に株式は無価値になる。他方で他企業が研究開発に失敗すると、独占企業として生産を継続することになる。このとき利潤\pi_nを配当として分配する。
　この株式の収益率がrとリスクフリーレートに等しい場合、無裁定条件として


\begin{aligned} \displaystyle{\frac{E[\pi_n+V_t]-V_{t-1}}{V_{t-1}}}&=\displaystyle{\frac{I(\pi_n+0)+(1-I)(\pi_n+V_t)-V_{t-1}}{V_{t-1}}}\\ &=\displaystyle{\frac{\pi_n+(V_t-V_{t-1})-IV_t}{V_{t-1}}}=r \end{aligned}


という条件を得る。

9.2.4　労働市場

　研究開発において財の生産を行う労働と研究開発に従事する労働の合計が労働供給に一致しなければならない。以下の仮定

  • 財の生産に対しても研究開発に対しても同一の賃金率wが支払われる。
  • 労働供給はLで一定である。


を置く。
　財を生産する独占企業の労働需要を説明する。新製品が開発された場合、旧製品が市場から駆逐され、市場には新製品のみが供給される。各財への需要は


\begin{aligned} x_j=\displaystyle{\frac{E/N}{p_j}}, j=2,3,\cdots,N \end{aligned}


で決定される。また各財の価格はp_n=\lambda p_{\mathrm{old}}=\lambda waである。
　更にいずれの産業でも独占企業の生産技術は同じであるから、どの財でもその価格はすべて同じになる。したがってそれぞれの財に対する需要は、


\begin{aligned} x_n\equiv x_j=\displaystyle{\frac{E/N}{\lambda wa}} \end{aligned}


のように同一水準に決定される。
　1単位の財を生産するためにはa単位の労働を投入する必要がある。すなわちx単位の生産を行う企業にはax単位の労働投入が必要になるから、ある独占企業の労働需要は


\begin{aligned} ax_n=\displaystyle{\frac{E/N}{\lambda w}} \end{aligned}


である。したがってN産業全体の独占企業の総労働需要L_x^Dは


\begin{aligned} L_x^D=Nx_n=\displaystyle{\frac{E}{\lambda w}} \end{aligned}


で得られる。
　一方で、研究開発に必要な労働は各産業につきa_IIであるから、総労働需要L_R^Dは


\begin{aligned} L_R^D=Na_II \end{aligned}


である。仮定から労働供給Lは一定であるから、労働市場の均衡条件は

\begin{aligned} L_x^D+L_R^D=\displaystyle{\frac{E}{\lambda w}}+Na_II=L \end{aligned}


である。

9.2.5　定常状態における均衡の分析

　株価の無裁定条件および労働市場の均衡条件を基に定常状態における最適な研究開発水準を求めることにする。労働市場の均衡条件

\begin{aligned} L_x^D+L_R^D=\displaystyle{\frac{E}{\lambda w}}+Na_II=L \end{aligned}

を書き換えることで、

\begin{aligned} \displaystyle{\frac{E}{w}}=\lambda L-\lambda Na_{I}I \end{aligned}

を得る。ここでの内生変数は研究開発水準Iおよび賃金率で基準化された家計の毎期の支出額E/wである。
　次に株価の無裁定条件

\begin{aligned} \displaystyle{\frac{\pi_n+(V_t-V_{t-1})-IV_t}{V_{t-1}}}=r \end{aligned}


について、\mathrm{Euler}方程式から定常状態では家計の支出が毎期で等しくなる、すなわちE_{t+1}=E_t, {}^{\forall}tであるから、利子率rは時間選好率\rhoに等しくなる。このときには株価も一定(V_{t+1}=V_t)になることから、定常状態における株価を\bar{V}とすれば

\begin{aligned} &\displaystyle{\frac{\pi_n+(\bar{V}\bar{V})-I\bar{V}}{\bar{V}}}=r\\ \Leftrightarrow&\displaystyle{\frac{\pi_n-I\bar{V}}{\bar{V}}}=\rho\\ \Leftrightarrow&(I+\rho)\bar{V}=\pi_n\\ \Leftrightarrow&\bar{V}=\displaystyle{\frac{\pi_n}{I+\rho}} \end{aligned}

を満たす。ここに研究開発を行う企業の株価*1\bar{V}=w a_Iを代入することで

\begin{aligned} w a_I=\displaystyle{\frac{\pi_n}{I+\rho}} \end{aligned}

を得る。
　独占企業の利潤\pi_nを求めるべく、新製品の需要x_n\equiv x_j=\displaystyle{\frac{E/N}{\lambda wa}}を新製品を生産する企業の利潤


\begin{aligned} \pi_n=(p_{\mathrm{new}}-wa)x_{n}=wa(\lambda-1)x_n \end{aligned}

に代入すると、

\begin{aligned} \pi_n&=wa(\lambda-1)\displaystyle{\frac{E/N}{\lambda wa}}\\ &=\displaystyle{\left(\frac{\lambda-1}{\lambda}\right)\frac{E}{N}} \end{aligned}

を得る。これらをまとめることで

\begin{aligned} &w a_I=\displaystyle{\frac{1}{I+\rho}}\displaystyle{\left(\frac{\lambda-1}{\lambda}\right)\frac{E}{N}}\\ \Leftrightarrow&\displaystyle{\frac{E}{w}}=\displaystyle{\frac{\lambda N a_I}{\lambda-1}}(I+\rho) \end{aligned}

が得られる。以上をまとめて以下が定常状態を表す。

\begin{aligned} \begin{cases} \displaystyle{\frac{E}{w}}&=\lambda L-\lambda Na_{I}I\\ \displaystyle{\frac{E}{w}}&=\displaystyle{\frac{\lambda N a_I}{\lambda-1}}(I+\rho) \end{cases} \end{aligned}

これを解くことで均衡研究開発水準I^{*}および均衡支出額\left(\displaystyle{\frac{E}{w}}\right)^{*}は

\begin{aligned} I^{*}&=\displaystyle{\frac{\lambda-1}{\lambda Na_{I}}}\left(L-\displaystyle{\frac{N a_{I}}{\lambda-1}}\rho\right),\\ \left(\displaystyle{\frac{E}{w}}\right)^{*}&=L-\displaystyle{\frac{N a_{I}\rho}{\lambda}} \end{aligned}

で与えられる。



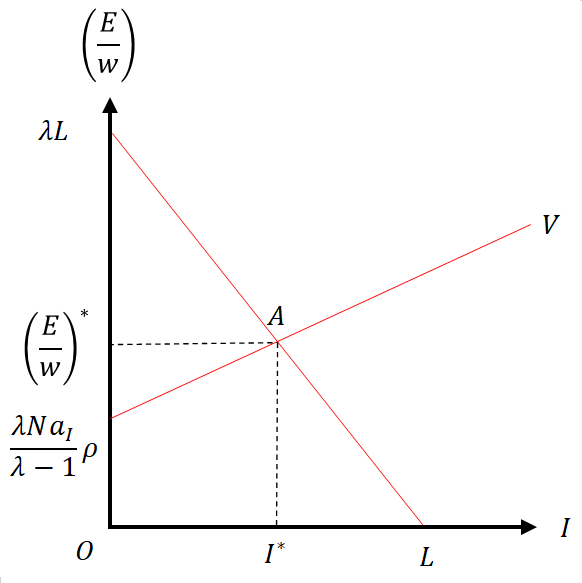
9.2.6　経済政策の効果

　\mathrm{Grossman\ and \ Helpman}のモデルでは、経済政策が研究開発(=技術進歩)に影響を与えることを反映している。
　政府が家計から一括固定税の形で徴税した資金を用いて企業の研究開発に補助金を支出する政策を行なうと仮定する。この政策の効果は、研究開発に必要な労働力a_Iが低下したと見なすことができる。これにより直線Lの傾きを低減させ、均衡研究開発水準を上げることができる。

9.2.7　規模効果

　研究開発には様々な資源を必要とするが、資源が豊富であればあるほど研究開発が促進され経済成長が高まると考えれる。この資源の豊富さが経済規模を表しているならば、経済規模が大きな経済ほど経済成長率が高くなることを意味する。このような効果を規模効果という。
　質のはしごモデルでは研究開発に必要な資源は労働供給量Lで、この意味では規模効果があると言える。
　しかし実証分析(\mathrm{Jones(1995)})によれば、現実には規模効果は存在しておらず、規模効果を持つ内生的成長理論は修正される必要があるという。規模効果が発生しないように研究開発の仕組みをどのように考えればよいか。このために

  • 研究開発に必要な費用が逓増的になることを仮定する
  • 研究開発の結果、財の種類も増加することを仮定する

前者を仮定したモデルは半内生的成長モデル、後者を仮定したモデルはハイブリッド・モデルと呼ばれる。

9.3　内生的成長理論のさまざまなモデル

9.3.1　公共サービスを含むモデル

　\mathrm{Barro(1990)}は政府が供給する公共サービス*2が労働生産性を上昇させるとの考えに基づき新しい経済成長モデルを提示した。このモデルでは生産関数を

\begin{aligned} Y_t=F(K_t,L_t,G_t) \end{aligned}

と設定する。ここでG_tは財の生産に投入される公共サービスである。ここに3つの仮定

  • 生産関数は\mathrm{Cobb-Douglas}型である：Y_t=AK_t^{\alpha}\left(L_tG_t\right)^{1-\alpha}
  • 人口成長はなく労働供給は一定である：L_t=1
  • 公共サービスのための財源は所得税で賄う：所得税率を\tauとしてG_t=\tau Y_t

をおく。以上の仮定から、

\begin{aligned} Y_t=AK_t^{\alpha}\left(\tau Y_t\right)^{1-\alpha} \end{aligned}

と表す。これを整理すると、

\begin{aligned} &Y_t^{\alpha}=A\tau^{1-\alpha}K_t^{\alpha}\\ \Leftrightarrow&Y_t=A^{\frac{1}{\alpha}}\tau^{\frac{1-\alpha}{\alpha}}K_t\equiv\tilde{A}K_t \end{aligned}

と定式化できる。
　\mathrm{Romer(1986)}は、経済全体に比べてその規模が小さいために個々の企業が行う資本蓄積から派生する労働生産性の上昇は個々の企業には認識されないと仮定することでこの問題を解決した。

9.3.2　AKモデル

　資本の限界生産性が一定である場合、定常状態でも1人当たり資本と\mathrm{GDP}成長率もまた一定になる。資本の限界生産性が一定であるような経済成長モデルを\mathrm{AK}モデルという。
　公共サービスを含むモデルは

\begin{aligned} Y_t=\tilde{A}K_t \end{aligned}

より、\mathrm{AK}モデルである。公共サービスが生産に貢献することにより、企業のうってき資本の限界生産性自体は逓減したとしても、資本全体の限界生産性は一定水準を保つことが可能になる。また経済政策の効果について、以下の結論を得る：

　政府は所得税率(\tau)を変化させることにより、経済成長に影響を与えることができる。

9.3.3　公共サービスを含むモデルの問題点

　公共サービスを考慮したモデルは、いくつかの問題点を有する：

  • 最適所得税率\tau^{*}の決定が困難である：

    　資本の経済生産性向上のために公共サービス増大は\tauの上昇をもたらす一方で家計の貯蓄に負の影響を与え、資本蓄積を抑制する
  • 公共サービスの混雑問題がある：

    　公共サービスの供給が充分でないと、公共サービスが資本の限界生産性へと直ちにつながらない
9.3.4　労働者の学習効果モデル

　労働者は生産活動を行う際に生産方法について学習を深め労働生産性を上昇させる。このような労働生産性の上昇を学習効果と呼ぶ。
　生産量の上昇に伴って学習効果が高まると考えられるため、技術変数をB_tとして生産関数は

\begin{aligned} \begin{cases} Y_t&=B_tK_t^{\alpha}L_t^{1-\alpha}\\ B_t&=A\left(\displaystyle{\frac{K_t}{L_t}}\right)^{1-\alpha},\ A\gt0 \end{cases} \end{aligned}

と定式化する。A\gt0より1人当たりの資本ストックが上昇すると生産量が上昇し学習効果が高まって生産性が上昇する。これを代入すると

\begin{aligned} Y_t&=B_tK_t^{\alpha}L_t^{1-\alpha}\\ &=A\left(\displaystyle{\frac{K_t}{L_t}}\right)^{1-\alpha}\left(K_t^{\alpha}L_t^{1-\alpha}\right)\\ &=AK_t \end{aligned}

が得られる、すなわちこのモデルも\mathrm{AK}モデルである。
　このモデルでは資本ストックの上昇が労働生産性を高めるため、経済政策が経済成長に与える効果に関して以下の結論が得られる。

　資本ストックを増やすような政策、たとえば設備投資に対する補助金は経済成長を高める効果を持つ。

　注意すべきは、設備投資を促進する政策が直ちに経済の更生を高めるとは限らない点である。

9.3.5　人的資本モデル

　人的資本とは労働者が持つ知識や技能などを一括りにした概念である。人的資本の蓄積にも教育や訓練が必要で、何らかの費用が掛かる。基準化された労働時間の上限1のうちuを財・サービスの生産に、1-uを教育や訓練に費やすことを仮定する。教育・訓練は、現在働いていたら得られたはずの賃金を費用として人的資本を蓄積することで将来の高い賃金をもたらす。

　人的資本H_tを含む生産関数を

\begin{aligned} Y_t&=F\left(K_t,H_t,L_t\right)=K_t^{\alpha}\left(u H_tL_t\right)^{1-\alpha}\\ \displaystyle{\frac{H_{t+1}-H_t}{H_t}}&=1-u \end{aligned}

と特定化する。
　ここでuH_tは技術進歩を考慮したソロー・モデルの生産関数

\begin{aligned} Y_t=F\left(K_t,A_t,L_t\right) \end{aligned}

における技術変数A_tに相当する。そのためこのモデルから得られる結論は技術進歩を考慮したソロー・モデルと同じである。ただし以下の2点で異なっている：

  • 1人当たり\mathrm{GDP}成長率は内生的に決定される
  • 1人当たり\mathrm{GDP}成長率を上昇させると現在の一人当たり\mathrm{GDP}が低下する

これらの議論から、以下のような結論を得られる：

　学校教育への投資、補助金は家計の人的資本の蓄積を促進し、\mathrm{GDP}成長率を上昇させる。

ただしこの結論は、完全競争市場の下でのモデルであることに注意しなければならない。

問題*3

1.　質のはしごモデル

　質のはしごモデルにおいて時間選好率ρが上昇した場合に最適研究水準I^{*}がどのように変化するかを述べよ。

2.　公共サービスを含む内生的成長モデル

　公共サービスを含む内生的成長モデルを考える。

(a) 家計の得る所得に\tau\ (0\lt \tau\lt1)の所得税率が掛けられるときに、家計のEuler方程式がどのようになるか計算せよ。
(b) (a)で求めたEuler方程式から消費の成長率を求めよ。
(c) 企業の利潤最大化条件および政府の予算制約式を用いて利子率を求めよ。
(d) 消費の成長率を最大にするような所得税率を求めよ。

3.　人的資本モデル

　人的資本モデルについて以下に答えよ。
　生産関数をY_t=K_t^{\alpha} (H_t L_t)^{1-\alpha}と仮定し、生産された財は家計が消費し、そのほかには設備投資[tx:I_t^K]もしくは人的資本への投資I_t^Hに用いられるものとする。資本ストック及び人的資源の資本減耗率は0、すなわち資本ストックはK_{t+1}=K_t+I_t^K、人的資本はH_{t+1}=H_t+I_t^Hであると仮定するとき、以下に答えよ。

(a) 資本ストックの限界生産性と人的資本の限界生産性をそれぞれ求めよ。
(b) 資本ストックの限界生産性と人的資本の限界生産性が等しくなるように企業がK_tおよびH_tの水準を定めることを直観的に説明せよ。
(c) 資本ストックの限界生産性と人的資本の限界生産性が等しくなるとき、本問の生産関数がAKモデルに一致することを示せ。

解答

1.　質のはしごモデル

  • 質のはしごモデルにおいて時間選好率ρが上昇した場合に最適研究水準I^{*}がどのように変化するかを述べよ。

　労働市場の均衡条件および株価の無裁定条件

\begin{aligned} \begin{cases} \displaystyle{\frac{E}{w}}=\lambda L-\lambda a_I NI \displaystyle{\frac{E}{w}}=\displaystyle{\frac{\lambda N a_I}{\lambda-1}(\rho+I)} \end{cases} \end{aligned}

から均衡I^{*}は

\begin{aligned} I^{*}&=\displaystyle{\frac{\lambda-1}{\lambda Na_{I}}}\left(L-\displaystyle{\frac{N a_{I}}{\lambda-1}}\rho\right),\\ \left(\displaystyle{\frac{E}{w}}\right)^{*}&=L-\displaystyle{\frac{N a_{I}\rho}{\lambda}} \end{aligned}

で与えられる。したがって時間選好率\rhoが上昇すると研究開発投資量Iは減少する。
　また定性的には、r=\rhoより、\rhoが上昇すると利子率が上昇することになる。したがって利子率が上昇すると株価が小さくなる。株価が小さくなることで、研究開発の収益が低く見積もられることになり、研究開発が減少する。

2.　公共サービスを含む内生的成長モデル

　公共サービスを含む内生的成長モデルを考える。

(a) 家計の得る所得に\tau\ (0\lt \tau\lt1)の所得税率が掛けられるときに、家計のEuler方程式がどのようになるか計算せよ。
(b) (a)で求めたEuler方程式から消費の成長率を求めよ。
(c) 企業の利潤最大化条件および政府の予算制約式を用いて利子率を求めよ。
(d) 消費の成長率を最大にするような所得税率を求めよ。
  • (a) 　家計の予算制約式は

    \begin{aligned}\begin{cases}(1-\tau)I_1&=S+C_1\\(1-\tau)I_2+(1-\tau)S&=C_2\end{cases}\end{aligned}

    で与えられる。Sを消去することで

    \begin{aligned}C_1+\displaystyle{\frac{1}{(1+r)(1-\tau)}C_2}=I\end{aligned}

    を得る。したがって\mathrm{Euler}方程式は

    \begin{aligned}\displaystyle{\frac{u^{\prime}\left(C_1\right)}{u^{\prime}\left(C_2\right)}}=\displaystyle{\frac{(1-\tau)(1+r)}{1+\rho}}\end{aligned}

    である。
  • (b)　対数型効用u(C)=\log Cを仮定すると、u^{\prime}(C)=\displaystyle{\frac{1}{C}}であるから、

    \begin{aligned}\displaystyle{\frac{C_2}{C_1}}=\displaystyle{\frac{(1-\tau)(1+r)}{1+\rho}}\end{aligned}

    である。したがって

    \begin{aligned}g^{C}&=\displaystyle{\frac{C_2-C_1}{C_1}}=\displaystyle{\frac{C_2}{C_1}}-1\\&=\displaystyle{\frac{(1-\tau)(1+r)}{1+\rho}}-1\\&=\displaystyle{\frac{-\tau+r-r\tau-\rho}{1+\rho}}\end{aligned}

    を得る。
  • (c) 　このモデルにおいて

    \begin{aligned}&Y_t=AK_t^{\alpha}G_t^{1-\alpha}=AK_t^{\alpha}\left(\tau Y_t\right)^{1-\alpha}\\\therefore\ \ &Y_t&=A^{\frac{1}{\alpha}}\tau^{\frac{1-\alpha}{\alpha}}K_t\end{aligned}

    である。企業が利潤最大化を図るとき、利子率は資本の限界生産率に等しくなるから、

    \begin{aligned}r&=\displaystyle{\frac{\partial Y_t}{\partial K_t}}\\&=A^{\frac{1}{\alpha}}\tau^{\frac{1-\alpha}{\alpha}}\end{aligned}

3.　人的資本モデル

　人的資本モデルについて以下に答えよ。
　生産関数をY_t=K_t^{\alpha} (H_t L_t)^{1-\alpha}と仮定し、生産された財は家計が消費し、そのほかには設備投資[tx:I_t^K]もしくは人的資本への投資I_t^Hに用いられるものとする。資本ストック及び人的資源の資本減耗率は0、すなわち資本ストックはK_{t+1}=K_t+I_t^K、人的資本はH_{t+1}=H_t+I_t^Hであると仮定するとき、以下に答えよ。

(a) 資本ストックの限界生産性と人的資本の限界生産性をそれぞれ求めよ。
(b) 資本ストックの限界生産性と人的資本の限界生産性が等しくなるように企業がK_tおよびH_tの水準を定めることを直観的に説明せよ。
(c) 資本ストックの限界生産性と人的資本の限界生産性が等しくなるとき、本問の生産関数がAKモデルに一致することを示せ。
  • (a)生産関数Y_t=K_t^{\alpha}\left(H_tL_t\right)^{1-\alpha}を資本ストックK_tおよび人的資本H_tそれぞれで偏微分することで

    \begin{aligned}\displaystyle{\frac{\partial Y_t}{\partial K_t}}&=\alpha K_t^{\alpha-1}\left(H_t L_t\right)^{1-\alpha}=\alpha\left(\displaystyle{\frac{H_tL_t}{K_t}}\right)^{1-\alpha}\\\displaystyle{\frac{\partial Y_t}{\partial H_t}}&=(1-\alpha)K_t^{\alpha}L_t\left(H_tL_t\right)^{-\alpha}=(1-\alpha)\left(\displaystyle{\frac{K_t}{H_tL_t}}\right)^{\alpha}\end{aligned}

    である。
  • (b) 資本と人的資本に投資を配分するときに、もし資本の限界生産性の方が人的資本の限界生産性よりも大きかったならば(逆の場合も同様に議論できる。)、このときI_t=I_t^K+I_t^Hが成り立っている下で、人的資本を1単位減らし代わりに資本を1単位増やすことで、

    \begin{aligned}\displaystyle{\frac{\partial Y_t}{\partial K_t}}-\displaystyle{\frac{\partial Y_t}{\partial H_t}}\gt0\end{aligned}

    だけ生産が増える(減る)。これは利潤最大化と矛盾する。したがって利潤最大化の観点から考えると限界生産性は等しくなければならない。
  • (c) 資本ストックの限界生産性および人的資本の限界生産性が等しいとき、(a)で示した式から

    \begin{aligned}&\alpha\left(\displaystyle{\frac{H_tL_t}{K_t}}\right)^{1-\alpha}=(1-\alpha)\left(\displaystyle{\frac{K_t}{H_tL_t}}\right)^{\alpha}\\\Leftrightarrow&H_t L_t=\displaystyle{\frac{1-\alpha}{\alpha}}K_t\end{aligned}

    を得る。これを生産関数に代入することで

    \begin{aligned}Y_t&=K_t^{\alpha}\left(H_t L_t\right)^{1-\alpha}\\&=K_t^{\alpha}\left(\displaystyle{\frac{1-\alpha}{\alpha}}K_t\right)^{1-\alpha}\\&=\left(\displaystyle{\frac{1-\alpha}{\alpha}}\right)^{1-\alpha}K_t\\&=\tilde{A}K_t,\ \tilde{A}=\left(\displaystyle{\frac{1-\alpha}{\alpha}}\right)^{1-\alpha}\end{aligned}

    が得られる。これはL_tが一定であれば\mathrm{AK}モデルであることに他ならない。

*1:上で示した。

*2:道路などの公共インフラ設備、治安維持のための警察、裁判所などを含んでいる。

*3:二神孝一・堀敬一（2017）「マクロ経済学　第2版」有斐閣　PP.229-230参照。

プライバシーポリシー お問い合わせ