証券投資(現代ポートフォリオ理論)をコンパクトに学ぶべく、比較的最近に発刊され薄めの本である
を参考に学んでいく。
- 前回:
4. 資本資産評価モデル
効率的フロンティア上のポートフォリオと同一のリスクを持つ資本市場線上のポートフォリオ
とを比較する。
ポートフォリオは効率的ポートフォリオ
と無リスク証券の一次結合で表される。明らかに同じリスクに対してポートフォリオ
のリターンはポートフォリオ
のリターンよりも大きい。仮定から投資家はリスク回避的であるから、ポートフォリオ
よりもポートフォリオ
を選好する。資本市場線のすべてのポートフォリオは接点ポートフォリオ
以外の効率的フロンティア上のポートフォリオに優越する。このように無リスク証券がある場合には、効率的フロンティア上の接点ポートフォリオ
と無リスク証券とを組み合わせた資本市場線上のポートフォリオを選択することとなる。
無差別曲線の下での資本市場線と効率的フロンティア

投資家が選択する資本市場線上の効率ポートフォリオのうちどれを選択するかは、投資家のリスク選好=効用関数に依存する。
上図では最も効用の大きい無差別曲線との接点を選択する。もし無リスク証券が無ければ、投資家は無差別曲線と効率的フロンティアとの接点
(接点ポートフォリオ)を選択する。
もし無リスク証券がある場合、無リスク証券と効率的フロンティア上の接点ポートフォリオとを組み合わせた資本市場線上のポートフォリオ
を選択する。
効率的市場においてはすべての投資家は期待リターンとそのリスクについて同一の情報をもつため、すべての投資家は無リスク証券に、市場ポートフォリオに
を持つ。
このポートフォリオの期待リターンは
である。またこのポートフォリオの分散は
である。
ここから
を得る。期待リターンにこれを代入することで
と書け、これは資本市場線に他ならない。
資本市場線を書き換えることで
を得る。これはポートフォリオのリスク1単位当たりの超過リターンが市場ポートフォリオのそれに等しいことを意味する。
4.2 CAPMの拡張
この節では無リスク資産をリスクフリーレートで借り入れるには限界が存在すると仮定する。
このとき、リスクフリーレートでの借り入れを全投資家ができるわけではない場合、資本市場線上のあらゆるポートフォリオが達成可能ではないから、すべての投資家が期待リターンおよびリスクについて同一の予想を持っていても効率的フロンティアへの接線ポートフォリオ上の市場ポートフォリオは全投資家にとって平均=分散モデルにおける最適ポートフォリオではない。
この場合のCAPMはBlack(1972)で提唱された。BlackのCAPMでは以下の性質で支えられている。
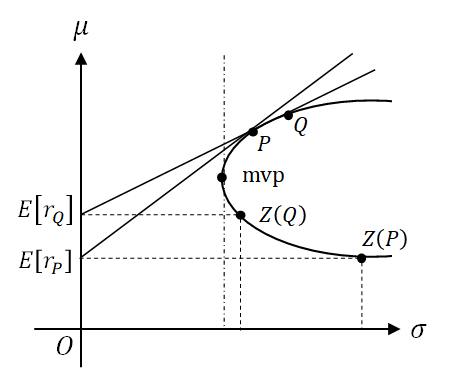
性質2で言及したポートフォリオは、効率的ポートフォリオと無相関であるから、ゼロベータ・ポートフォリオと呼ぶ。
BlackのCAPMにおいて任意の証券の期待リターン
は
で与えられる。
リスクフリーレートでの借入が不可能だと仮定すると、市場ポートフォリオでない2つのポートフォリオには
\end{aligned}
]
が成り立つ。これを資本配分線という。
借入が無い場合の資本配分線と資本市場線

いま2人の投資家を想定し、リスク回避的な投資家はリスクフリーレートで資金を貸すことでポートフォリオを組成し、もう一方のリスク許容的な投資家はポートフォリオ
を組成したとする。ポートフォリオ
はリスクフリーレート
から効率的フロンティアへの接点ポートフォリオである。
は
よりもリスクおよび期待リターンが大きい効率的ポートフォリオである。これらを一次結合したポートフォリオ
はリスクフリーレートでの借入ができないから、
のロングポートフォリオであるから、
の内分点である。
資本市場線がから成り立つならば、ポートフォリオ
は市場ポートフォリオである。
は効率的ポートフォリオであるから、性質1からポートフォリオ
は効率的市場ポートフォリオである。市場ポートフォリオ
は非効率的フロンティア上にゼロベータ・ポートフォリオ
をもち、性質2から
が成立する。成立3より任意の証券
の期待リターンは
に退化する。
上式はの代わりに
が効率的フロンティアに存在する限り、点
を接点とする資本市場線の縦軸
に等しい期待リターンをもつゼロベータ・ポートフォリオ
の期待リターン
が上式で表現できることを示した。このとき市場ポートフォリオ
とゼロベータ・ポートフォリオ
との相関係数は
である。
- 次回: