「大人の教養・知識・気付き」を伸ばすブログ

一流の大人（ビジネスマン、政治家、リーダー…）として知っておきたい、教養・社会動向を意外なところから取り上げ学ぶことで“気付く力”を伸ばすブログです。現在、コンサルタントの雛になるべく、少しずつ勉強中です(※2024年12月10日改訂)。

MENU

深くわかる金融(その14)：クレジット・デリバティブとは何ですか？

金融・ファイナンス 深くわかる金融

　今回はクレジット・デリバティブについて取り扱います。

今日のまとめ

  • 信用力(信用リスク)とは主体が債務を履行する蓋然性を表すものである。
  • クレジット・デリバティブとは、信用力を原資産としたデリバティブである。
  • 伝統的なクレジット商品は流動性に乏しいものが多いこともあり、クレジット・デリバティブはクレジット投資に有用な商品である。

1.　信用リスクとは何か

　クレジット・デリバティブを扱う前に、その投資対象となる信用リスクを説明する。

　信用リスクとは債務者による債務履行の蓋然性に起因するリスクをいう。具体的には、支払を取引相手が契約通りに実施しないことで損失を生じるリスクである。信用リスク顕現事由には債務者の倒産・債務不履行がある。たとえば銀行が企業に貸し出しているときに、貸出先が倒産して元本が毀損するリスクを指す。

　より具体的に述べると、たとえば元本が2億円でアモチ、半年後払で利率は0.5%、返済期間4年は担保は2,000万円分の預金があるものとする。このとき倒産しない場合とt=1.5にて債務者が倒産した場合を考えると以下のようになる。

2.　クレジット投資とは何か

　クレジット投資とは、取引相手の信用リスクを取ることの対価を受取るような投資をいう。
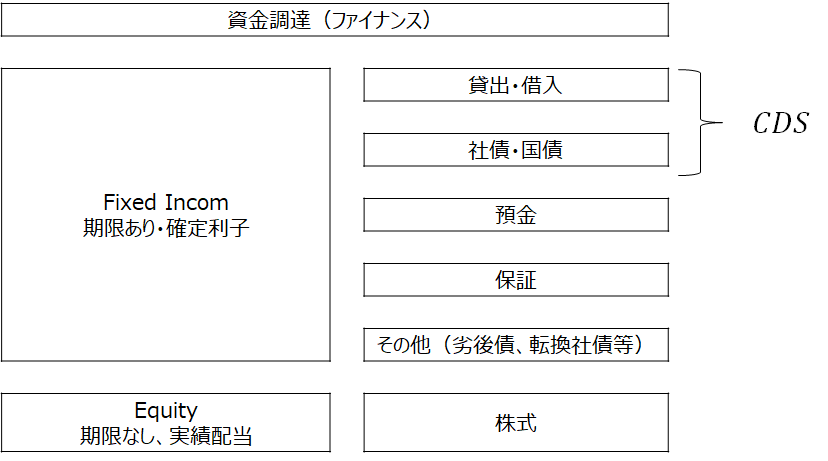
　伝統的なクレジット投資商品には、貸出・債券・信用保証・売掛債権がある。他方で近年開発された商品の中には、CDSの売買・クレジット・リンク債(対象企業の信用力変化に応じCFが変動する債券)がある。
　以降では、伝統的なクレジット商品には触れず、クレジット・デリバティブに焦点を当てる。

2.1.　クレジット・デリバティブとは

　クレジット・デリバティブとは信用力(Creditworthiness)を原資産としたデリバティブである。クレジット・デリバティブの原資産は、貸出、社債、売掛債権、信用保証といった信用力に投資する伝統的商品以外に企業や公的機関(Sovereign)自身の信用力がある。

2.2.　クレジット・デリバティブ取引の機能・特徴

　クレジット・デリバティブ取引には、様々な機能・特徴がある。

　 (1) 信用リスクの移転 信用リスクに対する伝統的投資商品は、一般に相対取引が多く流動性が低い。そこで信用リスク管理方法としてクレジット・デリバティブを売買することで、信用リスクの投資家は、自身の信用リスクに対するエクスポージャを機動的に調整することができる。
　 (2) 新市場の創造 CDSが活発的に取引されたりクレジット・デリバティブを組み込んだ債券を発行したりすることで、市場性のクレジット投資商品が少なかった日本において、多様な商品が提供されることとなった。
　 (3) 価格表示機能 信用リスクが市場で取引されることで、信用リスクの価値を推計することやデリバティブ価格から信用リスクの推計をリアルタイムで可能である。
　 (4) リスクが高い 伝統的金融商品の場合、発行者が発行する数以上の取引は不可能である一方で、デリバティブの場合、売買者がいる限り、無限に取引が可能である。そこで金融機関の過大なリスク・テイク先になる場合がある。


図表1　資金調達におけるCDSの範疇


図表2　クレジット商品の種類

2.3.　信用事由(Credit event)

　クレジット・デリバティブ(CDS)の取引対象となるクレジット・リスクの顕現を定義・明文化したものを信用事由という。信用事由はISDA(International Swaps and Derivative Association)の世界共通規格に則り決められる。
　信用事由は以下のように複数の事由があり、そのうち少なくとも1つが為されれば抵触したものと見なされる。

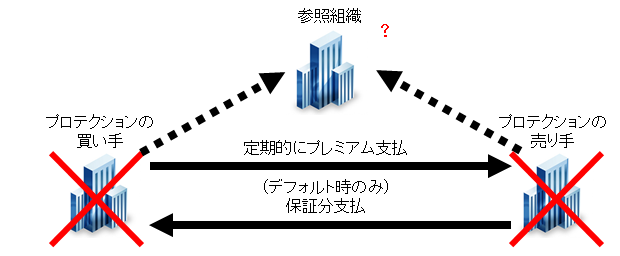
2.4.　カウンターパーティ・リスク(Counterparty Risk)

　スワップ取引特有のリスクとして、スワップ取引者がデフォルトするリスクを考慮する必要がある。買い手が満期までにデフォルトした場合、売り手はプレミアムを受取ることができなくなってしまう。一方で、売り手がデフォルトした場合、参照組織がデフォルトしても元本を得ることが出来なくなる。

2.5.　決済方法

　信用事由が起きた際の決済方法は3種類あるが、現在3つ目の入札決済が大半である。

　 (1) 現物決済 バイヤーは信用事由を起こした債務をセラーに渡す代わりに、取引額面金額全額に相当する現金をセラーから受け取る。
　 (2) 現金決済 信用事由発生後に回収率を設定、額面から回収額を差し引いた現金をセラーがバイヤーへ支払う。
　 (3) 入札決済 多数のディーラーが同一債務へ入札を行うことで回収率を設定の上、差額を決済する。

今では入札型が一般になっている。

3.　CDSとは何か

　CDSとは企業または公的機関の債務履行能力(Creditworthiness)を投資対象として取引するスワップ取引である。


図表3　CDSのスキームの模式図

3.1.　CDSの仕組み

  • 「CDSの買い手(Protection buyer)」は定期的に「プレミアム(Premium)」を「CDSの売り手(Protection seller)」へ支払う代わりに、「参照組織(Reference entity)」が予め定めた「デフォルト要件(信用事由: Credit event)」を満たした(起こした)場合、CDSの売り手から「想定元本(Notional principal)」などを受取ることができる。
  • 一部CDSは上場しており、投資家は自由に取引することができる*1。

　もし満期までに参照組織が信用事由に抵触しない場合、買い手は満期まで定期的にプレミアムを支払い売り手はプレミアムを受取ることで本CDSは契約を終了する。


　
　これに対し、満期前に参照組織が信用事由に抵触する場合、買い手はデフォルトするまで定期的にプレミアムを支払う。参照組織がデフォルトすると売り手は想定元本を買い手に支払い、本CDSは契約を終了する。

　たとえば主体A(プロテクションの買い手)が主体B(プロテクションの売り手)からCDSを購入した際の主体B側から見たのキャッシュフローを見る。なお本CDSは、参照組織をC社とし、取引期間は5年、想定元本は10億円であり、スプレッドは2.00\%(年1回、後払)とする。また簡単のため、信用事由に抵触した場合、想定元本を満額得られるものとする。このとき、満期まで信用事由に抵触しない場合(Case 1)とt=3にて信用事由に抵触する場合(Case 2)で以下のようなキャッシュフローが発生する。

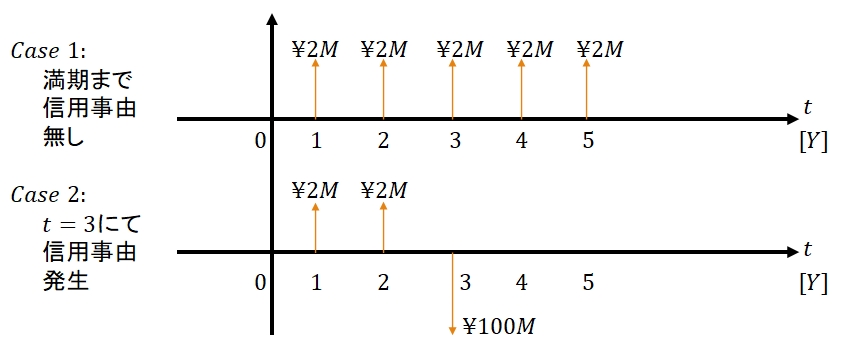
3.2.　CDSの機能

　CDSは多様な機能をもち、より柔軟なクレジット投資が可能となる。

　 (1) リスク移転機能 取引者間で信用リスクを柔軟かつ簡便に移転可能である。
　 (2) 取引条件の標準化による流動性 グローバルで規格が統一されていることから取引が容易であるため、市場参加者の拡大につながり、高い流動性を持つ。
　 (3) 価格形成機能 該当年限のCDSスプレッドを観測することで、信用リスクの価格を計測可能である。
　 (4) サイレント・ヘッジ機能 プロテクション・バイヤーは、自身の取引先の信用リスクを当該取引先に知らせることなくヘッジ可能である。
　 (5) 信用供与力創出機能 金融機関は貸出等の伝統的商品以外のクレジット投資商品を取り揃える事が可能である。
　 (6) リスク・プロファイル再構築機能 相対取引であるため、取引条件を柔軟に設定したクレジット投資商品を取り揃える事が可能である。

3.3.　CDSの参照組織候補

　CDSの参照組織には負債調達をしている(し得る)信用力を判定する意味のある企業や国家、自治体が該当する。参照組織の数および参照組織の注目点は商品に応じて異なる。

　 (1) シングル・ネーム 単一の主体を参照し、満期までにその主体が信用事由に抵触するか否かを焦点する。
　 (2) バスケット 複数の主体を参照し、満期までにどの主体が信用事由に抵触するかを焦点とする。
　 (3) ポートフォリオ 複数の主体を参照し、それらが信用事由に抵触して発生させた損失総額を焦点とする。

3.4.　CDSの種類

3.4.1.　シングル・ネームCDS

　最も簡単なCDSである。ある1つの主体を参照組織とし、同組織が満期までに信用事由に抵触するかを焦点とする。

3.4.2.　バスケット型

　複数の主体を参照し、満期までにどの主体が信用事由に抵触するかを焦点とするようなCDSをバスケット型という。
　ひとえにバスケット型といっても様々な種類がある。

　　 (1) リニア・バスケット バスケットに指定した複数銘柄に想定元本を按分して充てる。もしある参照組織が信用事由に抵触した場合、当該組織分の想定元本分のみ清算され、他の参照組織分は引き続き契約が続行する。すなわち、リニア・バスケット一つに投資することで、複数銘柄のシングル・ネームCDSに投資する(但し、エクスポージャは銘柄数で按分)のと同様の経済効果を与える。
　　 (2) ファースト・トゥ・デフォルト(First to default) バスケットに指定された複数銘柄のうち、ある参照組織がデフォルトした場合、当該組織に対するシングル・ネームCDSに全額投資した場合と同様の経済効果を与え、当該CDSの契約を終了する。参照組織間のデフォルト相関が低い場合、各参照組織のデフォルトが全てリスクとなるため、売り手にとっては、信用事由が起こりやすくなる(参考参照。)。
3.4.3.　ポートフォリオ型

　ポートフォリオ型(トランシェ型)にはファースト・ロス・プロテクション(First Loss Protection)がある。金額ベースでの損失を保証するCDSで、信用事由に至った銘柄に関係なく、当初定めた(Exposure\times LGD*2 )に至るまでの損失額すべてを保証するCDSである。

3.4.4.　インデックス型

　インデックス型は、複数のシングルネームCDSのプレミアムを一定のロジックで加工して作成したインデックスをプレミアムとするCDSである。当該CDSには、上場され活発に取引されているものが多い。

4.　その他クレジット投資商品

4.1.　クレジット・リンク債(Credit Linked Notes)

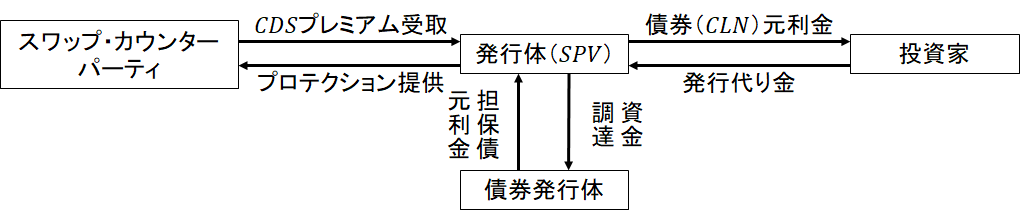
　通常の債券に発行体を参照するCDSを組み込み利回り向上を目指したクレジット投資商品をクレジット・リンク債という。

　　 (1) 投資家は発行体(アレンジャー銀行・SPV等)へ発行代り金を支払う。
　　 (2) 発行体(アレンジャー銀行・SPV等)は債券を購入すると共に、債券発行体の信用リスクの取得に必要なCDSのプロテクションをカウンターパーティへ売る。
　　 (3) これにより、債券発行体が信用事由を起こさなければ、債券からの元利金に加え、CDSのプレミアムを発行体が獲得し、それを経由して投資家はリターンを得ることができる。
　　 (4) しかし債券発行体が信用事由を生じさせた場合、債券自体のデフォルトによる信用リスクの顕現化に加え、CDSの支払による損失をも被ることになる。

4.2.　クレジット・リンク・ローン(Credit Linked Loan)

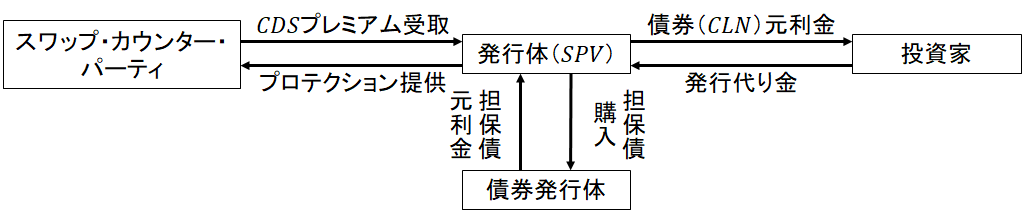
　貸出に貸出先を参照するCDSを組み込み利回り向上を目指したクレジット投資商品がクレジット・リンク・ローンである。前述したクレジット・リンク債と経済効用上は同一である。

　 (1) 投資家は発行体(アレンジャー銀行・SPV等)へ発行代り金を支払う。
　 (2) 発行体(アレンジャー銀行・SPV等)は貸出を行うと共に、貸出先の信用リスクの取得に必要なCDSのプロテクションをカウンターパーティへ売る。
　 (3) これにより、貸出先が信用事由を起こさなければ、当該貸出からの元利金に加え、CDSのプレミアムを発行体が獲得し、それを経由して投資家はリターンを得ることができる。
　 (4) しかし当該貸出先が信用事由を生じさせた場合、当該貸出のデフォルトによる信用リスクの顕現化に加え、CDSの支払による損失をも被ることになる。

4.3.　CDO(Collaborated Debt Obligation)

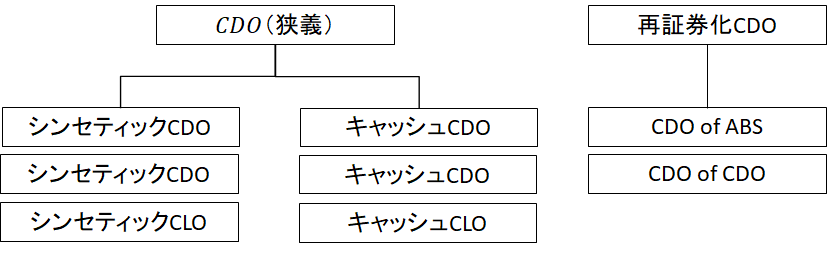
　複数の債務をひとつのポートフォリオとしてまとめあげ、そこから生じるキャッシュフローを複数の証券に切り分けて組成した金融商品をCDOという。原資産となる債務や切り分け方に応じ様々な種類のCDOがある(後述)。


4.4.　アセット・スワップ

　(固定金利)社債と変動化金利スワップを組み合わせた商品をアセット・スワップという。(固定金利)社債に普通に投資した場合、信用リスクに加えて金利変動リスクにも投資していることになる。そこでクーポンを打ち消すように固定金利支払、変動金利受取の変動化金利スワップを組み込むことで、投資家は信用リスクのみに投資できるようになる。

4.5.　トータル・リターン・スワップ(TROR)

　参照資産の価値変動を取引するスワップ取引をトータル・リターン・スワップ(TROR)という。通常、金融資産はインカムゲインを生むと共にキャピタルゲイン(ロス)を生む。トータル・リターン・スワップは両ゲインを交換する。

  • TRORぺイヤーは、期中に資産のインカムゲインを支払い、一方でTRORレシーバーはそれを受取る代わりにぺイヤーへ金利を支払う。
  • 満期には、参照資産が評価益を出していれば、TRORぺイヤーからレシーバーへ評価益分の金額が支払われる。一方、参照資産が評価損を出していれば、 TRORレシーバーからぺイヤーへ評価損分の金額が支払われる。

　TRORは参照資産を実際に売買することなく同資産の一定ポジションを構築したかのようなキャッシュフローを実現できるデリバティブである。

4.6.　CSO(Credit Spread Option)

　クレジット・スプレッドを原資産とするオプションをCSO(Credit Spread Option)という。

4.7.　DGP(Downgrade Protection)

　信用リスクの大きさを表章するものとして信用格付があるが、信用格付の格下げを参照する契約をDGPという。バイヤーは一定間隔でプレミアムをセラーに対して支払う代わりに、当初契約で定めた水準まで格付が下がった場合、セラーはバイヤーに一定金額を支払う。本取引は、カウンターパーティリスク上昇による評価損へのリスクヘッジに利用できる。

5.　CDO

5.1.　CDOの基本構造

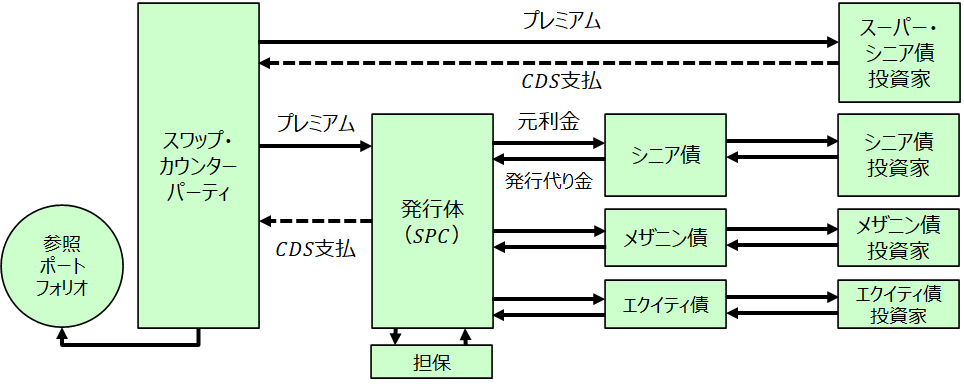
　CDOは証券化商品であり、証券化商品特有の各種要素を活用している。要約すると、

ポートフォリオ型のリスクを基に、異なる複数の信用補完水準の設定により優先劣後構造をつくり出し、発行体はリスクの異なるトランシェを発行する。各債権のキャッシュフローはカウンターパーティとの間でのスワップ取引で生み出され、元利金・諸経費の支払が行われる。全キャッシュフローは事前に定められた順番(Water Fall)に従い分配される。

5.2.　CDOの特徴(1)：ポートフォリオ

　CDOはポートフォリオとして原資産が複数存在することが最大の特徴である。社債や貸付債権(一般貸出、カードローン、オートローン、プロジェクトファイナンス、シンジケートローン等)、スワップ(CDS)、CDO、ABS等、様々な債権を原資産とする。原資産に応じて名前が変わる。たとえば貸付債権を原資産にするCDOはCLO(Collaborated Loan Obligation)などと呼ばれる。
　原資産数(個数)は組み入れる債権の種類により数件～数千件と様々である。

5.3.　CDOの特徴(2)：優先劣後構造

　証券化商品では複数債権のプールを基に、支払優先度合の異なるトランシェを発行するのが一般である。このトランシェは通常、シニア、メザニン、エクイティと呼ばれる(商品によっては更に分割する場合もある。)。
　利払タイミングになったら、まずシニア・トランシェの投資家に支払われる。次にメザニン・トランシェの投資家に支払われ、最後エクイティ・トランシェの投資家に支払われる。特にシンセティックCDO(上述)では、スーパー・シニアをシニアの上位に設ける場合がある。

5.4.　CDOの特徴(3)：発行体

　CDOの発行体はSPVである。これにより倒産隔離を図る。SPVは通常、ケイマン諸島、バミューダ諸島、キプロスなどのタックス・ヘイブンに設立されることが多い。

5.5.　CDOの特徴(4)：担保

　SPVが受取った発行代り金は、担保資産の購入に充てられる。

5.6.　CDOの特徴(5)：ウォーターフォール

　証券化商品は通常、全ての支払に対し順番が定められている(5.3.を参照。)。

5.7.　シンセティックCDO

　参照クレジット資産がCDSによって組成されるCDOをシンセティックCDOという。

6.　CDSを用いた信用リスク評価

　クレジット・デリバティブは信用力を取引する商品であるため、その価格は参照組織(資産)の信用力を反映しているはずである。そこで、クレジット・デリバティブの価格をモニタリングすることで、参照組織(資産)の信用力変化をモニタリングすることができる。
　ただしクレジット・デリバティブは相対取引で取引されることが大半であるため、流動性が低く信用力以外の情報が価格に織り込まれている場合があり、また価格情報が一般に公開されていないことが多い。

6.1.　CDSと信用力

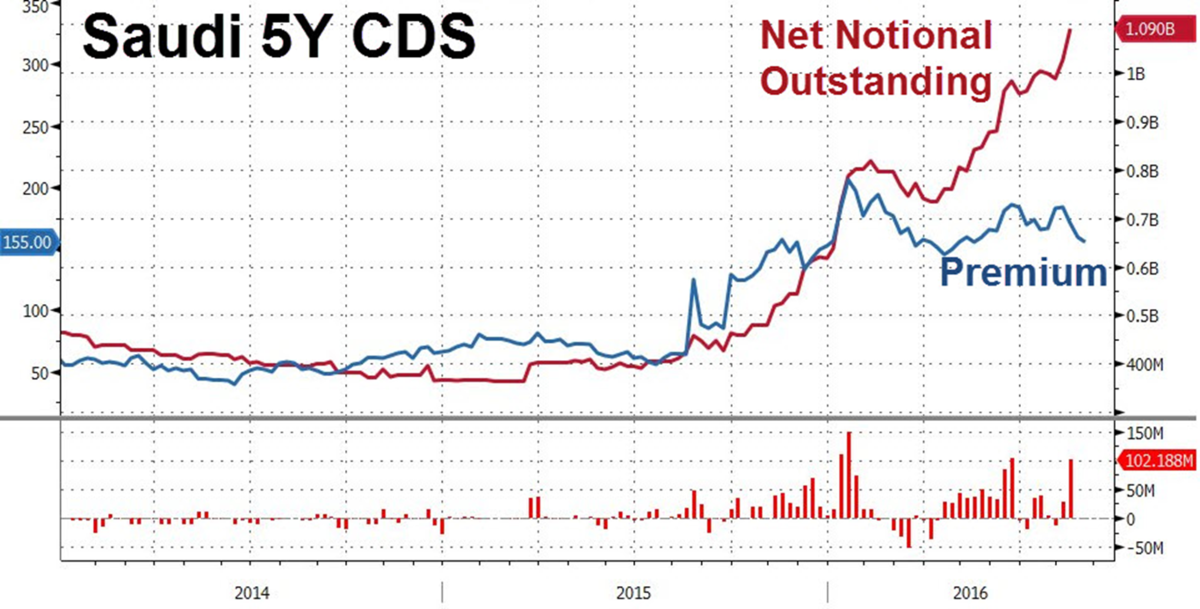
　CDSの場合、上場している商品の場合、流動性が高いこと、商品性が単純で参照組織の信用力が素直に反映されているため、CDSスプレッドから信用力を読み取ることができる。


図表4　事例：サウジアラビア・ソブリンCDS5年物


図表5　事例： S&P/ISDA Eurozone Developed Nation Sovereign CDS OTR Index

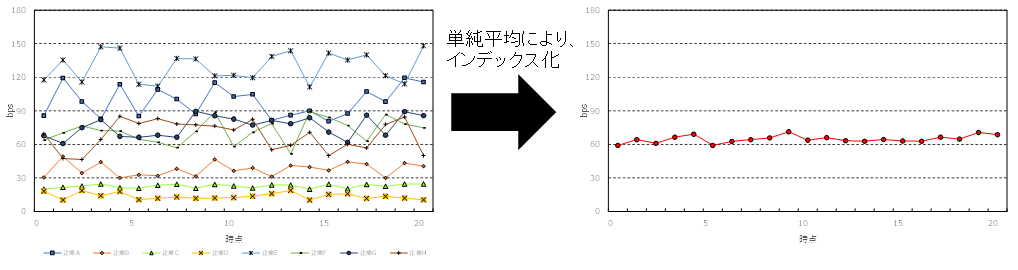
　図表5のS&P/ISDA Eurozone Developed Nation Sovereign CDS OTR Indexは、欧州圏の発展途上国のソブリンCDSを基に作成したインデックスである。2011年3月以降、欧州債務危機を受け欧州圏の信用力が下がっていると判断されていたことが読み取れる。

　クレジット・デリバティブは、信用力に対する投資商品であるため、投資対象の信用リスクを反映した価格設定がなされているはずである。そこで、一定のロジックの下で、市場で観測された価格から投資対象の信用リスクを逆算できるはずである。ここでは、最も単純なクレジット・デリバティブである𝐶𝐷𝑆を用いて、投資対象となる企業・ソブリンの信用リスク評価が可能であることを示す。
　このときCDSはスワップ取引であるから、バイヤーとセラーのお互いが受け取ることになる期待キャッシュフローの現在価値が一致することに注意する(逆に、理論的にはそうなるようにスプレッドが設定されているはずである。)。以降では、簡便法を考えることとする。

  • 現時点(t=0[Y])に約定するシングル・ネームCDS Cを考える。このCは
　 (1) 参照機関(企業またはソブリン):A社[国 etc.]
　 (2) 満期:T
　 (3) プレミアム:s[bps]
　 (4) 支払回数:年2回払(t=1/2,\cdots,T-1/2,T)
  • Cの参照機関であるAに対して、

　(1)Aがデフォルトした際の回収率(債務のうち自身で回収できる額の割合)：\delta
　(2)Aのデフォルト時点を表す確率変数：\tau
　(3)(リスク中立下で)Aがある時点tまでにデフォルトする確率：PD(t)=P\{\tau\leq t\}

  • ディスカウント・ファクター：D(t)=\exp\left(\displaystyle{\int_{0}^{t} r(s) ds}\right)とする。このときr(t)はスポット・レートで、 \tauと独立であると仮定する。
  • セラー・バイヤーのカウンターパーティ・リスクは考慮しない。

　現時点でCDS Cの市場価格(スプレッド)がsだったとする。このsは、市場が合理的な場合、 セラーもバイヤーも損をしないような無裁定な価格設定がなされているはずである。すなわちAがデフォルトした場合にバイヤーがセラーから受け取ることになる金額の現在価値とAがデフォルトするまでもしくは満期を迎えるまで(t=\min\{\tau,T\})にセラーがバイヤーから受け取るプレミアムの現在価値は一致しなければならない。そこでセラー側の現在価値とバイヤー側の現在価値をそれぞれ計算し恒等式を立てることで、信用力に関する等式を導く。
　セラーが受け取るのは、デフォルトするか満期が到来するまでの一定時点にバイヤーから支払われるプレミアムである。想定元本をPとおくと、ある時点tにセラーが受け取るプレミアムは、1bps=0.01\%であり、年2回払いであることに注意すれば


\begin{aligned} CF_{S}(t)=\displaystyle{\frac{s}{20000}}P\boldsymbol{1}_{\{\tau\gt t\}}(t) \end{aligned}


である。ここで、tに依存するある集合Sに対し\boldsymbol{1}_{S}(t)は


\begin{aligned} \boldsymbol{1}_{S(t)}(t)=\begin{cases} 1,\ &t\in S,\\ 0,\ &t\notin S,\\ \end{cases} \end{aligned}


で定義される(Indicator functionという。)。すなわち\boldsymbol{1}_{\{\tau\gt t\}}(t)は時点tにデフォルトしていない(\tau\gt t)ならば1を、Aがデフォルトしている(\tau\leq t)ならば0を返す関数である。
　したがってセラーが受け取るキャッシュフローの現在価値PV_Sは、 セラーがプレミアムを受け取ることのできる回数をk(=\lfloor T/2\rfloor：満期を2で割ったときの商)とすると、


\begin{aligned} PV_S&=\mathbb{E}^{P}\left[\displaystyle{\sum_{i=1}^{k}D\left(\displaystyle{\frac{i}{2}}\right)\frac{s}{20000}P\boldsymbol{1}_{\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}}}\right]\\ &=\displaystyle{\frac{sP}{20000}}\ \mathbb{E}^{P}\left[\displaystyle{\sum_{i=1}^{k}D\left(\displaystyle{\frac{i}{2}}\right)\boldsymbol{1}_{\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}}}\right]\\ &=\displaystyle{\frac{sP}{20000}\sum_{i=1}^{k}}\ \mathbb{E}^{P}\left[\displaystyle{D\left(\displaystyle{\frac{i}{2}}\right)\boldsymbol{1}_{\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}}}\right]\\ &=\displaystyle{\frac{sP}{20000}\sum_{i=1}^{k}}\left\{\displaystyle{D\left(\displaystyle{\frac{i}{2}}\right)\mathbb{E}^{P}\left[\boldsymbol{1}_{\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}}\right]}\right\}\\ &=\displaystyle{\frac{sP}{20000}\sum_{i=1}^{k}}\left\{\displaystyle{D\left(\displaystyle{\frac{i}{2}}\right)P\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}}\right\}\\ &=\displaystyle{\frac{sP}{20000}\sum_{i=1}^{k}}\left\{\displaystyle{D\left(\displaystyle{\frac{i}{2}}\right)\left(1-PD\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}\right)}\right\} \end{aligned}


すなわち割引後の受取キャッシュフローの大きさを、受取時点の生存確率で加重平均したものがセラーの受取キャッシュフローの現在価値となる。
　一方でバイヤーが受け取るのは、デフォルト時点にセラーから支払われる、想定元本のうち回収できなかった部分(1-\delta)Pである。したがってある時点tにバイヤーが受け取るキャッシュフローは、


\begin{aligned} {CF}_{B}(t)=(1-\delta)P\boldsymbol{1}_{\{\tau\leq t+dt|\tau\geq t\}}(t) \end{aligned}


である。ここで\{\tau\leq t+dt|\tau\geq t\}とは、t=tとなる直前まではデフォルトしていないが、微小時間dt後(つまり、 \tau=Tになった途端)デフォルトするという事象である*3。
　したがって、バイヤーが受け取るキャッシュフローの現在価値PV_{B}は、


\begin{aligned} PV_B&=\mathbb{E}^{P}\left[\displaystyle{\int_{t}^{T}D(u)(1-\delta)P\boldsymbol{1}_{\{\tau\leq t+dt|\tau\geq t\}}(u)du}\right]\\ &=(1-\delta)P\displaystyle{\int_{t}^{T}D(u)dP\{\tau\leq u\}} \end{aligned}


である。
　CDSはスワップ取引であるから、セラー側の受け取るキャッシュフローの現在価値とバイヤー側の受け取るキャッシュフローの現在価値は等しくなければならない。したがって、


\begin{aligned} s=\displaystyle{\frac{20000(1-\delta)\displaystyle{\int_{t}^{T}D(u)dP\{\tau\leq u\}}}{\displaystyle{\sum_{i=1}^{k}}\left\{\displaystyle{D\left(\displaystyle{\frac{i}{2}}\right)\left(1-PD\left\{\tau\gt\displaystyle{\frac{i}{2}}\right\}\right)}\right\}}} \end{aligned}

6.2.　CDSと信用力：簡便法

　ここでは簡便的にデフォルト率を求める方法を考える。デフォルトし得る債券の金利y(t)とリスクフリーレートr_f(t)からデフォルト率を以下のとおりで推計できる。


\begin{aligned} &\ (1-PD(T))Pe^{-T\cdot r_f(T)}+PD(T)\delta e^{-T\cdot r_f(T)}=\delta P e^{-T\cdot y(T)}\\ \therefore &\ PD(T)=\displaystyle{\frac{1-\exp\left\{-(y(T)-r_f(T))T\right\}}{1-\delta}} \end{aligned}


ここでy(T)-r_f(T)はクレジット・スプレッドを表しているため、これを年限T年のCDSスプレッドs_T(但し、ここでは実数表示)に置き換えることで、


\begin{aligned} PD(T)=\displaystyle{\frac{1-e^{-sT}}{1-\delta}} \end{aligned}


を得ることができる。逆に言えば、


\begin{aligned} &\ \log\left\{1-(1-\delta)PD(T)\right\}=-sT\\ \therefore&\ s=-\displaystyle{\frac{\log\left\{1-(1-\delta)PD(T)\right\}}{T}} \end{aligned}

参考

  • ファースト・トゥ・デフォルトとデフォルト相関

    　極端な例を考えてみよう。あるファースト・トゥ・デフォルトCDSがn社を参照しているとする。簡単のため、全組織が満期Tまでにデフォルトする確率を一律2\%とする。すなわち\tau_iをある参照組織i,i=1,2,\cdots,nのデフォルト時点とする。すなわち

\begin{aligned} P\{\tau_i\leq T\}=0.02 \end{aligned}

である。
　もし全ての参照組織のデフォルトが独立に起きる場合(このとき、デフォルト相関は0である。)、このCDSが信用事由に至る確率は、少なくとも一つの参照組織がデフォルトに至る確率であるから、

\begin{aligned} P\left\{\displaystyle{\bigcup_{i\in\{1,\cdots,n\}}\{\tau_i\leq T\}}\right\}=\displaystyle{\sum_{i=1}^{n}}P\{\tau_i\leq T\}=0.02n \end{aligned}

である。
　一方で、全参照組織のデフォルト相関が1であるならば、この𝐶𝐷𝑆が信用事由に至る確率は、少なくともある一つの参照組織がデフォルトに至る確率であるから、

\begin{aligned} P\left\{\displaystyle{\bigcup_{i\in\{1,\cdots,n\}}\{\tau_i\leq T\}}\right\}=P\{\tau_1\leq T\}=0.02 \end{aligned}

である。
　以上から、参照組織の単独のデフォルト率のみならず、デフォルト相関もCDSが信用事由を起こす確率に影響することが分かった。なおCDSが信用事由を起こす確率は当然プレミアムに跳ねてくる。デフォルト率が高い方がプレミアムは高い。すなわち今回の事例では、前者の方がプレミアムが高くなり後者の方はプレミアムは低くなる。

参考文献

*1:日本では非上場。

*2:エクスポージャは(信用)リスクに晒されている金額である。貸出であれば元本であり、CDSであれば想定元本である。LGDはLoss Given Defaultの略で、デフォルトしたときに毀損する比率(1-\displaystyle{\frac{担保カバー額}{エクスポージャ}})で計算できる。

*3:なぜこのような記述をするかというと、連続変数に対する確率には、P\{X=x\}=0、つまりある値ちょうどを取る確率は0となるという性質があり、上記事象を正確に表現するには、上の表記を用いて計算時に正確にデフォルト確率を織り込む必要があるからである。

プライバシーポリシー お問い合わせ