深くわかる金融(その13)：スワップ取引とは何ですか？ - 「大人の教養・知識・気付き」を伸ばすブログ

　今回はスワップ取引について取り扱います。

今日のまとめ

「約定時点で現在価値の等しいキャッシュフローの交換」をスワップ取引という。

スワップ取引は取引者双方が支払うないし受け取る資金のうち割安な方の調達コストによる含み益を関係者で分配することで関係者に利益をもたらし得る取引である。

1.　スワップ取引のための基礎事項
2.　スワップ取引とは
3.　スワップ取引のプライシング
4.　リーマンショック後の変化
- 4.1.　マルチ・イールド・カーブ
- 4.2.　信用評価調整・ファンディング評価調整
参考
参考文献

1.　スワップ取引のための基礎事項

　スワップ取引を学ぶために必要な事項として、キャッシュフローおよび割引を取り扱う。

1.1.　キャッシュフロー

　キャッシュフローとは、お金について、

金額：いくら
時点：いつ
方向：受取(+）、支払(-）

を同時に併せた概念である。
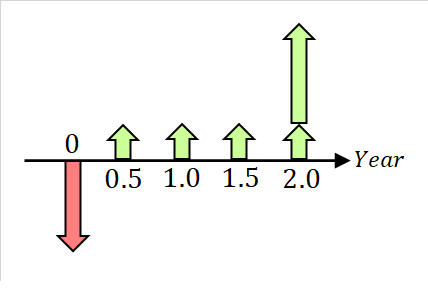
　たとえば半年払満期2年の国債のキャッシュフローを図示すると以下のようになる。

図表1　キャッシュフローのイメージ(例：利付2年債)

また個々の発生する金額もキャッシュフローと呼ぶ。

1.2.　現在価値と割引

　受取(支払）が異なる期間で生じる場合は、その期間における時間価値を価格に織り込む必要がある。
　具体的には、将来のある時点 $s=t$ における価値(将来価値：Future Value）が $X$ であるようなキャッシュフローの現在時点( $s=0$ )の価値(現在価値：Present Value）は、適当な金利 $r$ を用いて

$\begin{aligned} PV=\displaystyle{\frac{X}{\left(1+\displaystyle{\frac{r}{n}}\right)^{nt}}}=X\cdot D(t) \end{aligned}$

として行う。現在価値を計算することを割引くといい、上式の $D(t)$ を割引因子(discount factor)という。

図表2　現在価値のイメージ

1.2.1.　NPV

　複数のキャッシュフローを発生させる資産の現在価値をどう考えればよいか。これは異なる年限の割引債を複数保有(もしくは空売り）することと経済効果的に等しいため、それぞれのキャッシュフローを割引き、和を取ってやればよい。すなわち時点 $t=t_1,t_2,\cdots,t_n$ にそれぞれキャッシュフロー $CF(t_1),CF(t_2),\cdots,CF(t_n)$ が発生するような資産の現在価値 $NPV$ は

$\begin{aligned} NPV=\displaystyle{\sum_{i=1}^{n}D(t_i)CF(t_i)} \end{aligned}$

で表される。これを正味現在価値(NPV: net present value）という。

1.3.　スポットレート

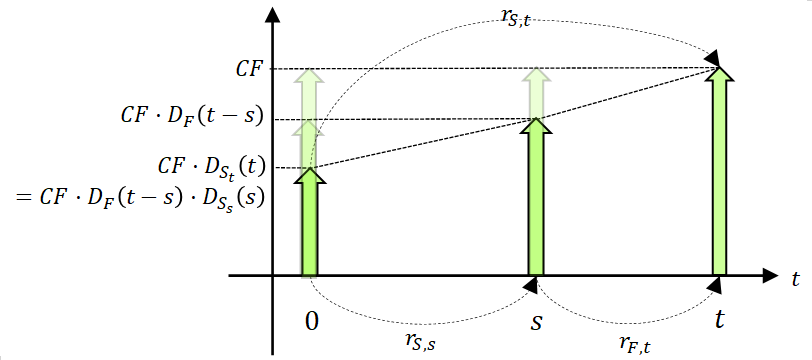
　適当な金利 $r$ と書いたが、どのような金利 $r$ を用いるのが適当なのか。割引に用いるべき金利は、割引したい資産の将来時点に対応したスポット・レートである。
　スポット・スタート(現時点スタート)のゼロ・クーポン・キャッシュフロー(割引債のキャッシュ・フロー)に内在する金利(implied interest rate）をスポット・レートという。キャッシュ・フローに内在する金利とは、将来時点のキャッシュ・フローと0時点のキャッシュ・フローを等しくする(正味現在価値 $NPV=0$ とする*1 )ような金利をいう。すなわち満期が時点 $t=t$ に到来する、額面が $FV$ であるような割引債の価格が現時点( $t=0$ )において $PV$ であるとき、

$\begin{aligned} &NPV=-PV+FV\cdot D(t)=0\\ \Leftrightarrow&D(t)=\displaystyle{\frac{PV}{FV}}\\ \Leftrightarrow&\displaystyle{\frac{1}{(1+r)^t}}=\displaystyle{\frac{PV}{FV}}\\ \Leftrightarrow&(1+r)^t=\displaystyle{\frac{FV}{PV}}\\ \Leftrightarrow&r=\sqrt[t]{\displaystyle{\frac{FV}{PV}}}-1\\ \end{aligned}$

　スポット・レートは市場で直接観察できないため、市場で観察可能な金利から算出する。たとえば国債からスポット・レートを誘導する*2。
　このとき、ディスカウント・ファクターは時間価値を考慮するために用いることから、用いる金利はスポット・レートが割引く対象と同程度の各種リスクを備えた金利でなければならない。たとえばLIBORを参照するスワップ取引を割引くためのスポット・レートはLIBORから誘導するかLIBORと同程度のリスクを内包するように調整する。

1.4　フォワード・レート

　将来スタートのゼロ・クーポン・レートに内在する金利をフォワード・レートという
　フォワード・レートは金利における裁定取引を考えるために重要である。時点 $t=0$ で時点 $t=s$ までスポット・レートで運用すると同時に、時点 $t=s$ スタートで時点 $t=t$ までの金利先物を購入したとする。このとき無裁定であれば、金利先物の金利(これはフォワード・レートになる）は、時点 $t=0$ で時点 $t=t$ までスポット・レートで運用するときの総資産額と等しくなるように決まる。
　時点 $t=0$ から時点 $t=k$ までで適用されるスポットレートを $r_{S_k}$ とし金利 $r_{X_Y}$ を用いたディスカウント・ファクターを $D_{X_Y}(t)$ とするとき、時点 $t=s$ スタートで時点 $t=t$ までのフォワードレート $r_{f,s,t}$ は、簡単のために時点 $t=t$ に発生するキャッシュフローの大きさを $1$ としたときに

$\begin{aligned} &D_{S_t}(t)=D_{F_{t-s}}(t-s) D_{S_s}(s)\\ \Leftrightarrow&\displaystyle{\frac{1}{(1+r_{S_t})^{t}}}=\displaystyle{\frac{1}{(1+r_{F_{t-s}})^{t-s}}}\displaystyle{\frac{1}{(1+r_{S_s})^{s}}}\\ \Leftrightarrow&(1+r_{S_t})^{t}=(1+r_{F_{t-s}})^{t-s}(1+r_{S_s})^{s}\\ \Leftrightarrow&(1+r_{F_{t-s}})^{t-s}=\displaystyle{\frac{(1+r_{S_t})^{t}}{(1+r_{S_s})^{s}}}\\ \Leftrightarrow&r_{F_{t-s}}=\sqrt[t-s]{\displaystyle{\frac{(1+r_{S_t})^{t}}{(1+r_{S_s})^{s}}}}-1\\ \end{aligned}$

が成り立つ。左辺は $t=0$ から $t=t$ までスポットレート $r_{S_t}$ で運用すると額が $1$ になるということを、右辺は $t=0$ から $t=s$ までスポットレート $r_{S_s}$ で運用した後に $t=0$ で契約した $t=s$ から $t=t$ までの金利先物でフォワード・レート $r_{F_{t-s}}$ で運用したら額が $1$ になるということを意味し、無裁定であるからこれらは等しくなるはずである。

図表3　フォワードレートのイメージ*3

2.　スワップ取引とは

2.1.　スワップ取引の定義

　「約定時点で現在価値の等しいキャッシュフローの交換」をスワップ取引という。
　スワップを分類するには2つの観点に注目すれば十分である：

(1)	通貨	同じ通貨の異なる金利を交換するスワップ取引を金利スワップ、異なる通貨の元本と金利を交換するスワップ取引を通貨スワップという。
(2)	元本	スワップの期間を通じて元本が一定であるスワップをブレット、元本が逓減するものをアモチゼーション、一旦逓増した後逓減するスワップをローラー・コースターと呼ぶ。

2.2.　スワップ取引の歴史

　初めてのスワップ取引は1981年8月に米ソロモン・ブラザーズが仲介したものである。

図表4　世界初のスワップ取引の模式図

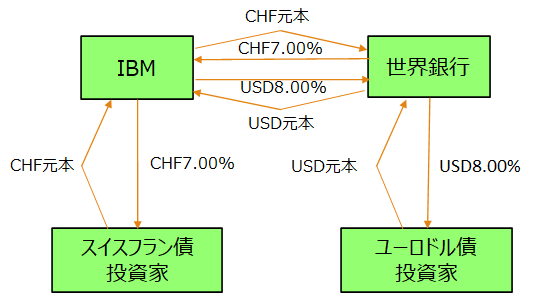
　IBMは当時、米国市場で調達しきれない米ドルを、債券発行により調達したスイスフランをドル転することで調達していた。為替ヘッジを行わないでいた所、スイスフラン安になり含み益が発生。一方で世界銀行はスイスフラン調達を希望するものの、世銀債についてスイスフラン市場において過剰感があることから断念し、ユーロドルを調達した。そこでソロモンブラザーズは、IBMと世界銀行との間で両通貨のスワップ取引を提案した。スワップ取引を通じて、両者はそれぞれ自身にとって割安な通貨で資金調達をしつつ必要な通貨を調達でき、為替リスクから解放された。またIBMは為替含み益が出ている時点のレートで交換できたことから、含み益を確定することが出来た。
　1982年には、マーケット・メーカーが登場し、流動性の高い米国債によるヘッジを基に米ドルを中心としてスワップ取引が活性化した。日本では、1984年の解禁と共にスワップ取引を開始した。

2.3.　スワップ取引の意義

　スワップ取引は「現在価値が等しいキャッシュ・フローの交換」であるから、一方が利益を得、他方が損失を被る取引というわけではない。では、スワップ取引で得られる利益はどこから来たものなのか。
　スワップ取引の損益は以下の２つから現れたと考えられる。

(1)	割安な原調達の利益がスワップ取引により顕在化した。
(2)	資金調達者が何らかのリスクを負ったことで、当面の利益を得たのみにすぎない。

具体的な事例で考えてみよう。

図表5　スワップ取引の仮想例

図表6　上記スワップ取引における各企業の資金調達コスト

資金調達コスト	固定金利	変動金利
企業A	$5.00\%$	OISレート $+0.10\%$
企業B	$6.50\%$	OISレート $+1.00\%$

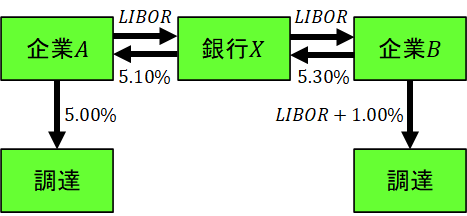
　企業A,Bの資金調達コストが図表6のとおりであったとして銀行Xは図表5のスワップを提案した。
　すると企業Aは資金調達コストを

$\begin{aligned} \left|−OIS−5.00\%+5.10\%\right|=\left|OIS−0.10\%\right| \end{aligned}$

企業Bは資金調達コストを

$\begin{aligned} \left|−(OIS+1.00\%)+OIS−5.30\%\right|=6.30\% \end{aligned}$

と、共に $0.20\%$ コストを削減することができた*4。また銀行Xは $0.20\%$ の利益を得た。
　これらの総削減コストおよび銀行収益の総計 $0.60\%$ の原資は、企業A,B双方が相対的に割安な原調達を選んだときに削減し得る金利

$\begin{aligned} \left\{(6.50\%)+(OIS+0.10\%)\right\}−\left\{(5.00\%)+(OIS+1.00\%)\right\}=0.60\% \end{aligned}$

である。このようにスワップ取引の意義はスワップ締結者双方の割安な原調達の利益を関係者で分配できることだと言える。

2.4.　スワップ取引の種類

2.4.1.　金利 スワップ

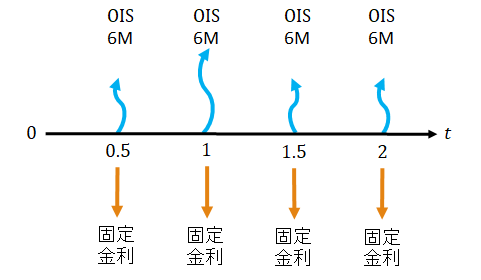
　現在価値の等しい同一通貨間の異なるキャッシュフローを交換するものを金利スワップという。プレーン・バニラ・スワップ *5のキャッシュフローはたとえば以下のようになる。

	通貨	日本円
	想定元本	￥1,000,000,000
	契約開始日	20XX年4月1日
	期間	2年
	参照金利(固定)	2.20%( $a$ /365,半年後払)
	参照金利(変動)	OISレート6か月物( $a$ /360,半年後払)
	金利支払日	毎年4月1日および10月1日
	固定金利支払者	企業A
	変動金利支払者	銀行B

図表7　企業Aから見たプレーン・バニラ・スワップのキャッシュフロー

　この取引は企業Aと銀行Bとの間で締結された金利スワップであり、企業Aが固定金利を銀行Bへ支払い、逆に銀行Bが支払った変動金利を企業Aが受け取るというスキームである。
　まず本契約は日本円を取引に用いる通貨とする。想定元本は￥1,000,000,000である(ただし金利スワップでは為替リスクが無いために両者の債権債務を相殺することで通常、元本は交換しない。それぞれが支払う金利額を計算するのに用いる。)。本契約は20XX年4月1日から2年間継続し、その間に契約で定めたタイミングでキャッシュフローを交換する。
　固定金利側の参照金利は $2.20\%$ /年であり、直前の利払日から次の利払日までの期間*6はその期間の実日数である $a$ を365*7で割った( $a$ /365)年とし、他方で変動金利側の参照金利はOISレート6か月物であり、直前の利払日から次の利払日までの期間はその期間の実日数である $a$ を360*8で割った( $a$ /360)年とする。金利支払日は毎年4月1日および10月1日であり、契約開始から終了期間である2年後までに到来した4月1日および10月1日にキャッシュフローの交換を行うということである*9。ただしいずれの金利も後払であるから、参照期間が終わってから支払う*10。
　企業A側は、 $i$ 回目の利払日において、直前の利払時点(または契約時点(ここでは20XX年4月1日) ) $t=t_{i-1}$ から今回の利払時点 $t=t_{i}$ までの日数 $a=[tex:t=t_{i}$ - $t=t_{i-1}$ ]に対応する固定利息

$\begin{aligned} 固定金利\times \displaystyle{\frac{a}{365}}\times 元本=2.20\%/年\times \displaystyle{\frac{a}{365}}\times 1,000,000,000 \end{aligned}$

を銀行Bへ支払い、その代わりにこの取引に対応する時点(この取引は後払であるから $t=t_{i-1}$ 時点)のOISレート6か月物 $r_{OIS,t_{i-1}}$ から計算する変動利息

$\begin{aligned} 変動金利\times \displaystyle{\frac{a}{360}}\times 元本=r_{OIS,t_{i-1}}[\%/年]\times \displaystyle{\frac{a}{360}}\times 1,000,000,000 \end{aligned}$

を受け取る*11。

2.4.2.　通貨スワップ

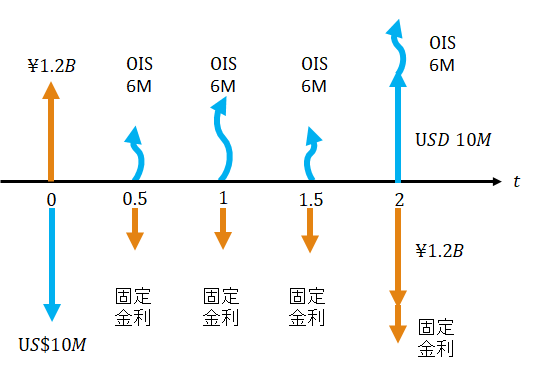
　現在価値の等しい異なる通貨間の異なるキャッシュ・フローを交換するスワップ取引を通貨スワップという。簡単な通貨スワップのキャッシュ・フローを見る。

	通貨	日本円、米ドル
	想定元本	JPY1,200,000,000/USD10,000,000
	契約開始日	20XX年4月1日
	期間	2年
	参照金利(日本円)	2.00%( $a$ /365,半年後払)
	参照金利(米ドル)	OISレート6か月物( $a$ /360,半年後払)
	金利支払日	毎年4月1日および10月1日
	日本円支払者 (米ドル受取者)	企業A
	米ドル支払者 (日本円受取者)	銀行B

図表8　企業Aから見た通貨スワップのキャッシュフロー

　この取引は企業Aと銀行Bとの間で日本円と米ドルとを対象として締結された通貨スワップであり、企業Aは自身のもつ米ドルを支払う代わりに日本円を受け取り、その日本円を運用した結果(金利)を相手に支払う代わりに当初支払った米ドルの運用結果(金利)を受け取り、満期には運用結果および当初支払った米ドルを受け取る*12というスキームである。
　想定元本は￥1,200,000,000／$10,000,000である(外貨取引は相殺は行わないのが慣習であるから、金利スワップとは異なり元本も交換する。)。本契約は20XX年4月1日から2年間継続し、その間に契約で定めたタイミングでキャッシュフローを交換する。
　日本円金利側の参照金利は $2.00\%$ /年であり、直前の利払日から次の利払日までの期間*13はその期間の実日数である $a$ を365で割った( $a$ /365)年とし、他方で米ドル金利側の参照金利はOISレート6か月物であり、直前の利払日から次の利払日までの期間はその期間の実日数である $a$ を360で割った( $a$ /360)年とする。金利支払日は毎年4月1日および10月1日であり、契約開始から終了期間である2年後までに到来した4月1日および10月1日にキャッシュフローの交換を行うということである*14。ただしいずれの金利も後払であるから、参照期間が終わってから支払う。

2.4.3.　スワップション

　権利行使日に条件を満たしているとスワップ取引が開始する権利を売買する取引をスワップションという。すなわちスワップ取引を原資産とするオプションである。

	ペイヤーズ・スワップション	固定金利払い、変動金利受けのスワップを行うスワップション。
	レシーバーズ・スワップション	変動金利払い、固定金利受けのスワップを行うスワップション。

2.4.4.　コーラブル・スワップ

　取引当事者の一方が事前に定めた期日に当該スワップを終了させる権利を通常の金利スワップに付与した金利スワップをコーラブル・スワップという。たとえば事業法人Aと銀行B間で締結し、銀行Bが売りポジションで、銀行Bの支払額が一定以上に達した際、銀行Bが当該スワップを終了できるコーラブル・スワップがある。銀行Bは自分が一定以上の損失を被る場合に当該契約を終了させられる権利を持ち有利であるため、事業法人Aへ支払う金利が終了権利の無い金利スワップよりも上乗せする。

2.4.5.　イールドカーブ スワップ

　参照期間と利払期間が異なる金利を交換する金利スワップをイールドカーブスワップという。たとえば片方は「OISレート6ヶ月物+スプレッド」、もう片方は「各々の金利計算期間の開始日2営業日前の10年物スワップ・レート：とするものが考えられる。長短金利差が今後大きくなると予想する場合のヘッジに利用する。

2.4.6.　インフレーションスワップ

　『「変動金利+スプレッド」または「固定金利」』と「インフレーション指標に連動する指数から算出される金額」を交換するスワップをインフレーションスワップという。

2.4.7.　ベーシススワップ

　適用金利が両者とも変動金利となっている通貨スワップをベーシススワップという。

2.4.8.　OISスワップ

　「固定金利」と「無担保コールオーバーナイト金利(OIS金利)から計算される変動金利」を交換する金利スワップをOISスワップという。無担保コールオーバーナイト金利は、コール市場で担保なしで資金を借り、翌営業日に返済する取引の金利である。変動金利は以下で計算する：

$\begin{aligned} \left\{\prod_{i=1}^{M}(1+O_i\delta_i)-1\right\}\times \displaystyle{\frac{365}{a}} \end{aligned}$

(1)	$M$	当該金利計算期間における銀行営業日の日数を表すための添字。
(2)	$O_i$	$i$ 番目の銀行営業日付の無担保コールオーバーナイト金利。
(3)	$\delta_i$	$i$ 番目の銀行営業日付の無担保コールオーバーナイト金利が適用される実日数÷365(デイ・カウント・フラクション)。
(4)	$a$	当該金利計算期間の実日数。

3.　スワップ取引のプライシング

　スワップ取引において各種条件を定めることをプライシングという。特に(金利)スワップにおいて固定金利(スワップ・レート)を決定することを指す。
　具体的にはその他条件を決めた後に正味現在価値が理論的に $0$ になるようにスワップの条件を見つけることをいい、変動金利は契約時点では未定であるから確率モデルを導入し確率を加味した現在価値を算出することでスワップ・レートを決定する。
　またスワップ取引の価値を決めるとは、スワップ取引の正味現在価値を算出することをいう。契約時点ではスワップ取引の定義からその正味現在価値は $0$ である。しかし契約後(たとえば決算のための時価評価時点)は正になったり負になったりする。

　以下、簡単な例としてプレーン・バニラ・スワップのプライシングを考えることにしよう。満期 $T$ において額面 $1$ 単位通貨を受け取る割引債(discount bond)を考え、それの時点 $t(t\leq T)$ における価格を $v(t,T)$ とする。
　ここでは簡略化のために*15 スワップ取引として参照する変動金利 $r_S(t,t+\delta)$ をスポットレート

$\begin{aligned} 1+L(t,t+\delta)=\exp\left(\displaystyle{\int_{t}^{t+\delta}f(t,s) ds}\right)=\displaystyle{\frac{1}{v(t,t+\delta)}} \end{aligned}$

で定義する。ここで $f(t,s)$ は $t=t$ から $t=s$ までの瞬間スポット・レートである。
　時点列 $0\leq T_0\lt T_1\lt \cdots\lt T_{n-1}\lt T_n$ に対して $\delta_i=T_{i+1}-T_i$ とおくと、変動金利 $r_S(t,t+\delta)$ は

$\begin{aligned} r_S(T_i,T_{i+1})=\displaystyle{\frac{1-v(T_i,T_{i+1})}{\delta_i v(T_i,T_{i+1})}} \end{aligned}$

で書ける。

　現時点を $0$ とし、時点 $T_0$ からスタートする金利スワップを考え、スワップ・レート $s$ を求めたい。簡単化のため、想定元本を1単位円、利払間隔は $\delta$ 年で計 $n$ 回支払があるとする。
　固定金利支払側では、固定金利による利息 $S^{\prime}=\delta s$ を時点 $T_i=T_0+i\delta$ で支払うことになる。したがって、固定金利側の総支払利息の現在価値 $PV_{FIX}$ は、ディスカウント・ファクター $D(t)=v(0,t)$ となることから、

$\begin{aligned} PV_{FIX}&=S^{\prime}v(0,T_1)+\cdots+S^{\prime}v(0,T_n)\\ &=\delta S\displaystyle{\sum_{i=1}^{n} v(0,T_i)} \end{aligned}$

　一方で変動金利支払側は、時点 $T_{i+1}$ で変動金利による利息 $L_i^{\prime}=\delta r_S(T_i,T_{i+1})$ を支払うことになる。しかし、現時点( $t=0$ )では将来時点の $t=T_i$ に定まる $r_S(T_i,T_{i+1})$ は不確定である。
　そこで、割引債を用いて変動金利を複製してみる。以下の取引を考える。

	(1)	現時点 $0$ で満期 $T_0$ の割引債を購入し、同時に満期 $T_n$ の割引債を売却する。
	(2)	時点 $T_0$ において、(1)で購入した満期 $T_0$ の割引債による償還額である1単位円を時点 $T_0$ の変動金利 $r_S(T_0,T_1)$ (この時点では確定している。)で運用する。
	(3)	時点 $T_i,i=1,\cdots,n-1$ で得た利息 $L_{i-1}^{\prime}$ を支払い、元本1単位円を時点 $T_0$ の変動金利 $r_S(T_0,T_1)$ で運用する。
	(4)	時点 $T_n$ で得た利息 $L_{n−1}^{\prime}$ を支払い、元本1単位円で(1）で売却した割引債償還額を支払う。

　以上の取引は、現時点で満期 $T_0$ の割引債を受け取り、同時に満期 $T_n$ での割引債の償還額を支払うものであるから、その現在価値は、

$\begin{aligned} {PV}_{FR}=v(0,T_0)-v(0,T_n) \end{aligned}$

である。
　金利スワップ取引は、契約時点において固定金利側の現在価値と変動金利側の現在価値とが釣り合うように条件を定めることから、

$\begin{aligned} &\ {PV}_{FIX}={PV}_{FR}\\ \Leftrightarrow &\ v(0,T_0)-v(0,T_n)=\delta S\displaystyle{\sum_{i=1}^{n}v(0,T_i)}\\ \therefore&\ S=\displaystyle{\frac{v(0,T_0)-v(0,T_n)}{\delta\displaystyle{\sum_{i=1}^{n}v(0,T_i)}}} \end{aligned}$

　以上は非常に簡単化された一種の理想状態に基づくプライシングであるが、このような要領で条件に応じた数学モデルを用いてプライシングを行う。

4.　リーマンショック後の変化

4.1.　マルチ・イールド・カーブ

　リーマンショック後、信用リスクや流動性リスクを市場参加者が意識するようになった結果、市場参加者はリスクプレミアムを要求するようになり、テナー・ベーシス・スワップ *16、カレンシー・ベーシス・スワップ *17などのスプレッドに差が出るようになった。その結果、どの金利を基にイールド・カーブを構築したかによって、水準に無視できない差が生じるようになった。

4.2.　信用評価調整・ファンディング評価調整

　リーマンショック時に問題となったことの一つに、カウンターパーティ・リスクがあった。
　デリバティブ取引相手の信用力変化によるリスクをカウンターパーティ・リスクという。リーマンショック時には、カウンターパーティのデフォルトにより顕現化した損失額よりも、カウンターパーティの信用力悪化に伴う時価評価上の損失の方が大きかった。これを受け、デリバティブ取引では担保付取引が主流となった一方で、対一般事業法人取引では事務的な観点などから、担保付取引は困難であり、カウンターパーティリスクを $CVA$ (カウンターパーティ・リスクに係る期待損失額)としてデリバティブ時価に考慮することとなった。また自身の信用リスクを考慮した $DVA$ も用いられるようになった。
　また、リーマンショック後、金融機関の調達金利も金融機関毎にまちまちとなり、プライシングに用いる調達金利の差異がデリバティブ価値に大きく影響を与えるようになった。これへの対策として $FVA$ (担保金利と自己調達金利との差を調整するための、担保でカバーされない調達額分の調達金利と担保金利の差から生じる損益)を考慮させるようになった。すなわち

$\begin{aligned} 信用評価調整およびファンディング評価調整後のデリバティブ価値=&完全担保の場合のデリバティブ価値-CVA+DVA-FVA\\ =&完全担保の場合のデリバティブ価値-CVA+DVA-FCA+FBA \end{aligned}$

参考

連続複利

　Discount Factorを計算するときは、特に理論的に考える場合、計算の都合上連続複利を用いるのが普通である。
　年 $n$ 回の利払がある場合、Discount Factorは

$\begin{aligned} D(t)=\left(1+\displaystyle{\frac{r}{n}}\right)^{nt} \end{aligned}$

と書ける。これを一瞬一瞬に利息が発生すると考えると、

$\begin{aligned} D(t)=\left(1+\displaystyle{\frac{r}{n}}\right)^{nt}=\left(1+\displaystyle{\frac{r}{n}}\right)^{(\frac{r}{n})^{-1}rt}\rightarrow e^{-rt}(n\rightarrow\infty) \end{aligned}$

通常、 Discount Factorは $D(t)=e^{-rt}$ と書く。

スポット・レートの厳密な定義

　スポット・レートを厳密に定義する。リスクの無い、額面1単位円の支払を受ける割引債を考え、時点 $t(t\leq T)$ におけるこの割引債の価格を $v(t,T)$ とする。
　ここで考えている割引債はリスクが無いと仮定しているため、その価格は時間価値のみが考慮されたものとなっている。そこで、リスクが無い割引債から時間価値のみを純粋に考慮できる金利を抽出することを考える。連続複利を導入すると、割引債価格から金利が得られる。ここで得た金利を最終利回りまたはイールド(Yield）という。

$\begin{aligned} v(t,T)=e^{-(T-t)Y(t,T)} \end{aligned}$

　イールド(Yield）は以下のように変形できる。

$\begin{aligned} v(t,T)=e^{-(T-t)Y(t,T)}\Leftrightarrow Y(t,T)=-\displaystyle{\frac{\log v(t,T)}{T-t}} \end{aligned}$

　イールドにおいて $T\rightarrow t$ とした瞬間的な金利

$\begin{aligned} r(t)=-\displaystyle{\lim_{T\rightarrow t}\frac{\log v(t,T)}{T-t}}=-\displaystyle{\frac{\partial}{\partial T}\log v(t,T)|_{T=t}} \end{aligned}$

をスポット・レートと定義する。
　時点 $t$ において $T(T\gt t)$ までスポット・レートで1単位円を運用すると、

$\begin{aligned} B(t,T)=\exp\left(\displaystyle{\int_{t}^{T} r(s) ds}\right),\ 0\leq t\leq T \end{aligned}$

となる。これを銀行預金(money-market account)*18と呼ぶ。

スポット・レートとパー・レート

　債券価格が当該債券の $NPM$ を上回ることをオーバー・パー、下回ることをアンダー・パーといい、債券価格が $NPM$ と等しくなることをパーという。逆に債券価格が観測されたときに当該債券の $NPV$ をパーにするような金利をパーレート(スワップ・レート）という。
　パー・レートとスポット・レートは異なることに注意せよ。パー・レートはそれ単独で $NPV$ をパーにする金利である。すなわち、期中の割引金利は、CFの発生時点に関わらずパー・レートで一定と仮定することとなる。

$\begin{aligned} NPV=\displaystyle{\frac{1}{(1+r_{par})^{t_1}}}X_{t_1}+\displaystyle{\frac{1}{(1+r_{par})^{t_2}}}X_{t_2}+\cdots+\displaystyle{\frac{1}{(1+r_{par})^{t_k}}}X_{t_k} \end{aligned}$

一方、スポット・レートは発生時点に応じて異なる値を取り得る。

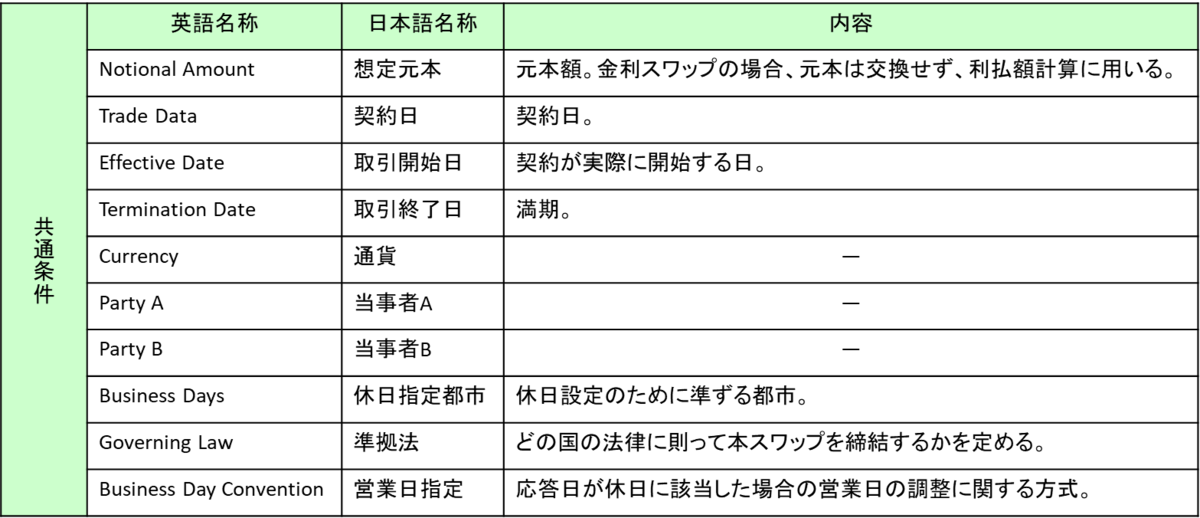
$\begin{aligned} NPV=\displaystyle{\frac{1}{(1+r_{Spot}(t_1))^{t_1}}}X_{t_1}+\displaystyle{\frac{1}{(1+r_{Spot}(t_2))^{t_2}}}X_{t_2}+\cdots+\displaystyle{\frac{1}{(1+r_{Spot}(t_k))^{t_k}}}X_{t_k} \end{aligned}$

スワップ取引の契約に掛かる諸用語

参考文献

木島正明(1999）「期間構造モデルと金利デリバティブ」朝倉書店
杉本浩一、福島良治、若林公子(2011）「スワップ取引のすべて　第4版」金融財政事情研究会
杉本浩一、福島良治、若林公子(2016）「スワップ取引のすべて　第5版」金融財政事情研究会

*1:価格は投資家からすれば支払うものであるから、負と見なす。

*2:誘導とは上式のように理論に当てはめて、必要なパラメータおよび価格から金利を計算することをいう。

*3:簡略化のためフォワードレートでのディスカウント・ファクターを $D_{F}$ で表している。

*4:企業Aは変動金利を選択しているため、絶対利率が大きくなる可能性はある。しかしそれは変動金利を受け入れたことに依るものであり、スワップ取引のリスクとは言えない。

*5:プレーン・バニラとは特段カスタマイズの無いといった意味の修飾語としてデリバティブ取引の呼称として用いる。スワップ取引では、一般にLIBORと固定金利を交換するような取引を指す。プレーン・バニラの対義語、すなわち基本的なスワップ取引とは異なるカスタマイズの入ったものをエキゾチックという。

*6:契約以後はじめての利払日の場合は、契約開始時点からの日数とする。

*7:これは実日数に関係なく1年=365日と見なすという意味である。

*8:これは実日数に関係なく1年=360日と見なすという意味である。

*9:無論、エキゾチックの中には支払時点をズラしたものも存在し得る。もっとも支払と受取の相殺が出来なくなるので複雑化するし、コストが掛かる。

*10:たとえば20XX年10月1日の支払は20XX4月1日から同9月30日までの期間に対する支払を行うものである。

*11:実際には、受取と支払を一部相殺し一方のみが支払うべき額を相手方に支払う。

*12:銀行から見ればすべて逆になる。すなわち自身のもつ日本円を支払う代わりに米ドルを受け取り、その米ドルを運用した運用した結果(金利)を相手に支払う代わりに当初支払った日本円の運用結果(金利)を受け取り、満期には運用結果および当初支払った日本円を受け取る。

*13:契約以後はじめての利払日の場合は、契約開始時点からの日数とする。

*14:元本と同様にこれは相殺しない。

*15:現実的ではない。

*16:同じ通貨の満期までの期間の異なる金利のスワップ。

*17:元本交換ありの通貨スワップ取引で交換金利が LIBOR( $+\alpha$ )となるもの。

*18:無論、本当の「銀行預金」という意味ではない。英語名が物語るように、スポット・レートで運用するという理想的な金利市場での運用結果を表している。誤訳ではないかと個人的には思っている。

1. スワップ取引のための基礎事項

1.1. キャッシュフロー

1.2. 現在価値と割引

1.2.1. NPV

1.3. スポットレート

1.4 フォワード・レート

2. スワップ取引とは

2.1. スワップ取引の定義

2.2. スワップ取引の歴史

2.3. スワップ取引の意義

2.4. スワップ取引の種類

2.4.1. 金利スワップ

2.4.2. 通貨スワップ

2.4.3. スワップション

2.4.4. コーラブル・スワップ

2.4.5. イールドカーブスワップ

2.4.6. インフレーションスワップ

2.4.7. ベーシススワップ

2.4.8. OISスワップ

3. スワップ取引のプライシング

4. リーマンショック後の変化

4.1. マルチ・イールド・カーブ

4.2. 信用評価調整・ファンディング評価調整

参考