深くわかる金融(その12)：コーポレート・ファイナンスとは何ですか？その1

　今回はコーポレート・ファイナンスの概要について取り扱います。

今日のまとめ

コーポレート・ファイナンスは「財務に関する意思決定を考える学問分野」である。

企業価値評価に先立ち、現在価値、割引を理解する必要がある。

企業価値評価では、まずファンダメンタルに着目する。

1.　金利の確認
2.　コーポレート・ファイナンスとは
- 2.1　コーポレート・ファイナンスの基本的概念
- 2.2　コーポレート・ファイナンスの焦点
3.　DCF法
4.　企業価値評価：ファンダメンタル手法
5.　企業価値評価
次回
参考文献

1.　金利の確認

1.1　金利とは何か

　過去稿でも取り扱ったとおり、金融取引とは現在の支払(受取)と将来の受取(支払)とを契約を通じて交換する取引である。この金融取引時の価格が「金利」に相当する。具体的には、現在支払う(受け取る)財と将来受取る(支払う)財との交換比率を表す。ここに現時点・将来時点との間の選好(時間選好率)と将来の不確実性に対する対価である「リスク・プレミアム」が加わる。
　金利はモノとカネとの間の相対価格である「物価」からも影響を受ける。経済的要因から決まる現時点の財と将来時点の財との交換比率を自然利子率(実質利子率)と呼び、ここに物価上昇率を上乗せしたものを名目利子率と呼ぶ。
　狭義の金融取引であれば、金利が直接的に介在する債券(やローン)の交換比率を考えればよいだろう。

1.2　金利の計算方法

　具体的に、金利をどうやって計算するか。

　割引債(期中のクーポン支払が無く、満期における償還のみ受取のある債券((狭義には、更にデフォルトが無く満期に確実に債務が履行されるものとする。)))を考える。このときの年間平均利益率を利回りといい、これが金利である。つまり、現時点における債券時価を $P$ 、満期償還額を $R$ 、満期までの期間を $n$ とおくと、利回り $r$ は、

$\begin{aligned} r=\displaystyle{\sqrt[n]{\frac{R}{P}}}\Longleftrightarrow P(1+r)^n=R \end{aligned}$

　ここでは年間平均利益率を利回りと定義したが、これが半年毎、1/3年毎、四半年毎、…、 $\displaystyle{\frac{1}{m}}$ 年毎になると、

$\begin{aligned} 1+\displaystyle{\frac{r}{m}}=\displaystyle{\sqrt[mn]{\frac{R}{P}}}\Longleftrightarrow P(1+\displaystyle{\frac{r}{m}})^{mn}=R \end{aligned}$

　より瞬間的に利益が発生する、つまり $m$ が大きくなっていく( $m\rightarrow\infty$ )と、

$\begin{aligned} (1+\displaystyle{\frac{r}{m}})^{mn}=(1+\displaystyle{\frac{r}{m}})^{\frac{m}{r}r\cdot n}\rightarrow e^{nr} \end{aligned}$

したがって

$\begin{aligned} &\ P e^{nr}=R\\ \Leftrightarrow&\ r=\displaystyle{\frac{1}{n} \log\left(\frac{R}{P}\right)} \end{aligned}$

となる。これを連続複利による金利(連続金利)という。
　利付債(満期の償還額に加え、期中に利息を受け取ることができる債券)の場合、満期までに都度都度支払われる利息に加え、購入額と償還額との差を加味する必要がある。一年間の利息額を $c$ とすると、

$\begin{aligned} r=\displaystyle{\frac{c+\displaystyle{\frac{R-P}{n}}}{P}} \end{aligned}$

であり、これを最終利回りと呼ぶ。日本では国債の発行利回りは、習慣的に最終利回りで表示する。
　一方で、期中に利息を再投資することによる収益を加味するために複利最終利回りも一般に用いられる。

$\begin{aligned} P(1+R)^n=c(1+r)^{n-1}+c(1+r)^{n-2}+\cdots+c(1+r)+R+c \end{aligned}$

　これは、現時点での時価 $P$ を満期までこの利回りで運用した場合の価値(左辺)と各時点で得られるクーポンおよび元金を満期までこの利回りで運用したときの総額(右辺)が等しくなるような利回りである。このように、購入額と金融商品のキャッシュフローの現在価値を等しくする、期間に関わらず一定値を取ると考える金利をパーレートとも呼ぶ。
これは $r$ に関する $n$ 次方程式であるから、通常、数値計算で根(解)を算出する。

1.3　リスク・フリー・レート

　流通市場で取引される債券の場合、現時点に取引するが将来時点から資金のやり取りが発生する先渡取引(先物取引)もある。これは、取引開始時点が満期となる債券をショート(売り)し、取引終了時点が満期となる債券をロングする(買う)場合の採算を計算することで利回りを計算する参照レートと呼ばれる標準的な金利に加え、金利スワップや金利先物等を用いて算出した完全な安全度を持つ仮想的な資産の金利をリスク・フリー・レートという。
　以上の手法を用いて、横軸を満期までの期間、縦軸をその期間に対応するリスク・フリー・レートとしてグラフ化することで、金利変化に対する人々の予想を概観することができる。リスク・フリー・レートに限らず、満期までの期間の異なる金利をグラフ化したものをイールド・カーブという。一般には、満期までの期間に応じて金利水準は変化するはずである。この満期までの期間と金利との関係を金利の期間構造という。

2.　コーポレート・ファイナンスとは

　コーポレート・ファイナンスは「財務に関する意思決定を考える学問分野」である。コーポレート・ファイナンスは「企業経営者の業務は企業価値および現在の株価を増加させることである」ことを前提とする。

2.1　コーポレート・ファイナンスの基本的概念

　更にコーポレート・ファイナンスは以下を基本的な考え方とする：

コーポレート・ファイナンスは企業価値の最大化に関する学問である。
資本の機会コストが投資に関する意思決定の水準を定める。
安全なおカネはリスクのあるおカネよりも価値がある。
投資の意思決定を賢明に行う方が、資金調達の意思決定よりも価値を生む。
良いガバナンスが重要となる。

　企業の意思決定は、事業を行うという意味で以下の二つに類別できる。

投資に関する意思決定：実物資産に投資を行うこと。　例：機械を購入する、人材に教育をするetc.
資金調達に関する意思決定：金融資産を売却し投資資本を調達すること。　例：株式を発行する、借入を受けるetc.

　コーポレート・ファイナンスの議論においては、企業は株主Principalの所有物であり、経営者は株主の代理で企業経営を行うAgentと見なす。したがって、経営者の業務は
自身が代理を務める株主利益の最大化となる。しかし、PrincipalとAgentの利害関係は一致するとは限らない。AgentがPrincipalの利益を最大化するための一連の問題をAgency問題という。なぜ経営者と株主(所有者)を分離するのか。それは、所有と経営の分離を通じて、以下が可能となるからである。

企業経営に秀でた人間に経営を委託することで、より利益を増すことが出来うる。
投資家が資金を引き揚げても、経営者不在にならず企業は存続が可能となる。
投資家は資金を引き揚げて、分散投資が図れるようになる。

　以上から、所有・経営の分離を維持しつつ、Agency問題を軽減することが、投資家の資産価値を高めることにつながると考えられる。

2.2　コーポレート・ファイナンスの焦点

　企業は、負債または株式発行(資本家による出資)で調達した資金を基に事業を行い(これは資金運用の観点から言えば営業ないし資産運用のための資産を購入することに相当する)、利益を出す。
　黒字赤字以前に資本コスト(企業が事業のために調達する資本にかかるコスト(後述))を上回る利益を出さなければ、企業は自転車操業を繰り返すのみで成長することはできない。また、事業リスクが高ければ、投資家は必然高いリターンを要求する。

図表1　財務における投資家と企業の関係性

　企業活動を通じて企業は売上を得るが、それは各ステークホルダーへ配分される。特に最後、株主へ配分される。株主に帰属する利益を最大化するためには売上を上げつつ、株主以外への配分額を最小化すればよい。

図表2　企業の利益構造(損益計算書)とステークホルダーとの配分関係

図表3　企業資源とコーポレート・ファイナンスの関係

3.　DCF法

　投資家が企業に投資するのは、収益の分配として将来キャッシュを受け取ることができるからである。したがって、投資家にとって、企業価値とは将来受け取ることが期待できるキャッシュの評価額である。企業が事業に投資するのも、その事業が将来キャッシュを生み出すからである。そこで、投資案件や企業の価値を将来キャッシュフローから評価する方法を導入する。
　将来キャッシュフローの評価では、お金には時間価値がある(お金は時間が経つにつれその価値を上げていく)ことを前提にしている。また投資に関する意思決定においては、投資で得られる利益の総額のみでなく、収益を得られるタイミングが重要となってくる。したがって、①キャッシュの金額の大きさ、②キャッシュ・イン(+)なのかキャッシュ・アウト(-)なのか、③基準時点から見ていつ時点に発生するのか、の3点がキャッシュフロー評価では焦点になる。

例：手許に投資資金を $10$ 億円保有している企業Aが以下の2つの事業のうちいずれかに携わるという意思決定を行なう状況を考える。

(1)	初期投資として $10$ 億円、追加投資として毎年 $4$ 億円が必要だが $11$ 年後に $50\%$ の確率で $100$ 億円が得られる事業。利益を得るまでの期間の資金調達さえできれば大きなリターンが期待できる。
(2)	初期投資に $11$ 億円かかるが、追加投資が不要で $1$ 年後から $12$ 年間、毎年 $1.5$ 億円だけ利益が得られる事業。初期時点で $1$ 億円調達できれば確実に利益があがる。

これらの選択に合理的に出来るようにする必要がある。
　将来に発生が予想される資金の出入りを、その資金の発生時点に応じた金利で割り引くことで現在価値を算出する方法をDiscounted Cash Flow(DCF)法という。この方法では、ある金融商品の理論価値(企業価値)は、当該資産(企業)が生み出すキャッシュフロー(キャッシュ・イン、キャッシュ・アウトを含)の割引現在価値の総和であると考える。

3.1　現在価値

　将来時点で発生するキャッシュフローがもし現時点で発生する場合に得られた場合に等価と見なすことが出来る価値を現在価値といい、金銭の時間的価値を勘案するために用いる。
　前述したように、キャッシュフローでは、

キャッシュの金額の大きさ
キャッシュ・イン(+)なのかキャッシュ・アウト(-)なのか
基準時点から見ていつ時点に発生するのか

の3点が焦点になる。現在価値はこの3点目を考慮するためのものである。
　具体的には、その価値評価に適当な金利 $r$ を持ち出し「割引く」ことになる。

3.2　ディスカウント・ファクター

　前節で扱った金利の議論を思い出されたい。たとえば連続複利 $r$ を考えるとして、現時点に $X(0)$ だけ投資したところ、将来時点 $t$ に $X(t)$ だけ収益が得られる取引を考えると、これらの価値の間に

$\begin{aligned} X(0)\exp\left(rt\right)=X(t) \end{aligned}$

が成り立つ。これは将来時点に得られる収益を中心に見れば、将来時点 $t=t$ に $X(t)$ だけ得るというのは、現時点 $t=0$ に $X(0)$ だけ得るのと価値として等価だということを意味する。この観点から式変形すると、

$\begin{aligned} X(0)=X(t)\exp\left(-rt\right) \end{aligned}$

が成り立つ。更に見方を変えれば、これは将来時点の価値をそれと等価な現在時点における価値に変換したと言える。そしてそれは上式では $\exp\left(-rt\right)$ に相当する。この $\exp\left(-rt\right)$ をディスカウント・ファクター(割引因子)と呼ぶ。
　これを時点 $t$ の関数として $DF(t)$ と書くこともある。連続複利であれば上述のように $DF(t)=\exp\left(-rt\right)$ とするが年 $k$ 回払と見なすならば

$\begin{aligned} DF(t)=\displaystyle{\frac{1}{\left(1+\frac{r}{k}\right)^{kt}}} \end{aligned}$

と書ける。連続複利にするのか否かは正しいか否かというよりは、その商品特性や評価において求める精度の良さに応じて決めればよい*1。
　ファイナンス理論では通常、価値とは現在価値 $PV$ を指す。

3.3　NPV

　前節で割引や現在価値を議論したが、では実際に金融資産や投資プロジェクトを評価する場合、それらが生み出すないし必要とする将来時点に発生するすべてのキャッシュフローのそれぞれの現在価値を評価しそれらを合算することで行う。この合算価値を正味現在価値(Net Present Value: NPV)といい、

$\begin{aligned} NPV=\displaystyle{\sum_i PV_{i}}=\displaystyle{\sum_i DF(t_i)\cdot CF(t_i)} \end{aligned}$

$PV_i$	時点 $t=t_i$ に発生するキャッシュフロー $i$ の現在価値
$DF(t_i)$	時点 $t=t_i$ のディスカウント・ファクター
$CF(t_i)$	時点 $t=t_i$ に発生するキャッシュフロー $i$ 。これが収益ならば正、投資(損失・支出)ならば負を取る。

で定義する。金融資産や投資プロジェクトの現在価値(評価価値)はこのNPVを用いる。

3.4　割引に利用する利回り

　割引に当たってどの金利を用いるべきか？シンプルな事案であれば、キャッシュフローの年限に対応する「スポット・レート」を用いる*2。
　スポット・スタート*3のキャッシュフロー(ゼロクーポン債 *4をスポット・レート(ゼロ・クーポン・レート、ゼロ・イールドとも言う)という。市場で観測できないため、国債の利回り、スワップ・レート等から年限別スポット・レートを導出する*5。

3.4.1　スポット・レートの算出例(1) 国債を利用する方法

　国債をリスクフリー(信用リスク等のリスクが上乗せされておらず、時間的価値のみが考慮されている状態)であると仮定し、ブートストラッピングにて算出する方法がスポット・レート算出方法として知られている。

(0)	市場から満期が $1$ 年未満であるゼロクーポン債の利回りを得、これを1年のスポット・レートとする*6。
(1)	市場から $1$ 年ゼロクーポン債の利回りを得、これを1年のスポット・レートとする。
(2)	$t=1,2,\cdots, 9$ について、 $\displaystyle{\frac{2k+1}{2}}$ 年のスポット・レートを、 $k$ 年のスポット・レートおよび $k+1$ 年のスポット・レートの平均と仮定する。利付国債は年2回払い(半年に1回支払)であることを踏まえつつ、パーレートをスポット・レートと見なして計算する。
(3)	(2),(3)を $k$ に関して繰り返す。以上で得た全年限のスポット・レートを補間*7して任意時点のスポット・レートを得る。

3.4.2　スポット・レートの算出例(2) スワップ・レートを利用する方法

　無リスク金利(OIS金利など)を参照するプレーン・バニラ・スワップのスワップ・レートからスポット・レートをブートストラッピング法にて算出する。考え方は国債と同様であるので省略する。

3.4.3　スポット・レートの算出例(3)　金利モデルを利用する方法

　金利に関する数理モデルを用いてスポット・レートを推定する。最も利便性が高く実務上でも頻用されるのは、Nelson-Siegelモデルである。
　本モデルでは、時点 $t$ における瞬間フォワード・レート・カーブ*8 $f(t)$ が

$\begin{aligned} f(t)=\beta_0+\beta_1\exp\left(-\displaystyle{\frac{t}{\tau}}\right)+\beta_2\left\{\displaystyle{\frac{t}{\tau}}\exp\left(-\displaystyle{\frac{t}{\tau}}\right)\right\} \end{aligned}$

で与えられるとする。
　スポット・レート $r(t)$ は瞬間フォワード・レート $f(t)$ を用いて

$\begin{aligned} r(t)=\displaystyle{\frac{1}{t}\int_{0}^{t}f(x)dx} \end{aligned}$

と書けるから、Nelson-Siegelモデルを用いるとスポット・レートは

$\begin{aligned} r(t)=&\displaystyle{\frac{1}{t}\int_{0}^{t}f(x)dx}=\displaystyle{\frac{1}{t}\int_{0}^{t}\left[\beta_0+\beta_1\exp\left(-\displaystyle{\frac{x}{\tau}}\right)+\beta_2\left\{\displaystyle{\frac{x}{\tau}}\exp\left(-\displaystyle{\frac{x}{\tau}}\right)\right\}\right]dx}\\ =&\beta_0+(\beta_1+\beta_2)\left(\displaystyle{\frac{\tau}{t}}\right)\left\{1-\exp\left(-\frac{t}{\tau}\right)\right\}-\beta_2\exp\left(-\frac{t}{\tau}\right) \end{aligned}$

で与えられる。
　市場で観測した金利からパラメータ $\beta_i,i=0,1,2,\tau$ を推定し、スポット・レートを推定すればよい。

3.4.4　現在価値の算出事例(1)　コンソル債

　元本償還がない代わりに永遠に利息支払が行われる債券をコンソル債という。コンソル債の理論価値を求めてみよう。
　あるコンソル債は年1回、クーポン $C$ (一定)が支払われるとする(これは契約により予め定まっている。)。スポット・レートは期間に関わらず $r$ (一定)だとするとき、このコンソル債の現在価値 $PV$ は、

$\begin{aligned} PV&=\displaystyle{\sum_{k=1}^{\infty}\frac{C}{(1+r)^k}}\\ &=\displaystyle{\lim_{n\rightarrow\infty}\frac{C}{1+r}\cdot \frac{1-\left(\displaystyle{\frac{1}{1+r}}\right)^{n-1}}{1-\left(\displaystyle{\frac{1}{1+r}}\right)}}\\ &=\displaystyle{\frac{C}{1+r}\lim_{n\rightarrow\infty}\frac{1-\left(\displaystyle{\frac{1}{1+r}}\right)^{n-1}}{1-\left(\displaystyle{\frac{1}{1+r}}\right)}}\\ &=\displaystyle{C\cdot \lim_{n\rightarrow\infty}\frac{1-\left(\displaystyle{\frac{1}{1+r}}\right)^{n-1}}{r}}\\ &=\displaystyle{\frac{C}{r}} \end{aligned}$

で与えられる。

3.4.5　現在価値の算出事例(2)　定率成長

　企業評価において、ゴーイング・コンサーン *9だと仮定し、配当を年1回 $C$ だけ支払うと仮定する。更にその配当が年間 $g\lt r$ で定率成長していくとする場合にこの企業を評価する。

$\begin{aligned} PV&=\displaystyle{\sum_{k=1}^{\infty} C\cdot \frac{(1+g)^k}{(1+r)^k}}\\ &=\displaystyle{\sum_{k=1}^{\infty} \frac{C(1+g)}{1+r}\cdot \frac{(1+g)^{k-1}}{(1+r)^{k-1}}}\\ &=\displaystyle{\sum_{k=1}^{\infty} \frac{C(1+g)}{1+r}\cdot \frac{1-\displaystyle{\left(\frac{1+g}{1+r}\right)^{k-1}}}{1-\left(\displaystyle{\frac{1+g}{1+r}}\right)}}\\ &=C(1+g)\displaystyle{\lim_{k\rightarrow\infty}\displaystyle{\frac{1-\left(\displaystyle{\frac{1+g}{1+r}}\right)^{k-1}}{(1+r)-(1+g)}}}\\ &=C\cdot \displaystyle{\lim_{k\rightarrow\infty}\frac{1-\left(\frac{1+g}{1+r}\right)^{k-1}}{r-g}}\\ &=\displaystyle{\frac{(1+g)C}{r-g}} \end{aligned}$

で評価できる。
　なお $g\gt r$ の場合には $\displaystyle{\frac{1+g}{1+r}}\gt1$ となるために $\left(\displaystyle{\frac{1+g}{1+r}}\right)^{n-1}\rightarrow\infty(n\rightarrow\infty)$ と発散する。

3.5　回収期間と内部収益率

　投資プロジェクト評価にはNPV以外にも回収期間または内部収益率を用いる方法もある。

3.5.1　回収期間

　投資金額が何年で回収できるかを算出しそれが目標値よりも小さい場合に投資を実行するという手順で行う評価方法が回収期間による投資判断である。但し、回収期間が短いことを評価するため、近視眼的な投資が行われやすくなるデメリットがある。

3.5.2　内部収益率

　他に $NPV=0$ となるような割引金利を逆に求め、その割引金利(内部収益率という)を比較するという手順で行う評価方法が内部収益率による投資判断である。これは割引率を用いる必要がない点で優れている。

$\begin{aligned} NPV=\displaystyle{\sum_{t}\frac{C_t}{(1+IRR)^{t}}}=0 \end{aligned}$

キャッシュインが多かったりキャッシュアウトが少なかったり、キャッシュインのタイミングが速かったりキャッシュアウトのタイミングが遅ければ内部収益率は大きくなる。

4.　企業価値評価：ファンダメンタル手法

　企業価値とは「将来に渡って優れた経済活動を実践している企業に対して社会がそれを評価し、与えた対価(=利益) の合計額(現在価値)」と定義できる。この定義による企業価値を「本源的価値」、「内在価値」とも呼ぶ。
　内在価値が株式市場で適切に評価されているのであれば株式価格に利益が適切に反映されているため、「株式時価総額＝内在価値」である。しかし一般には、これは成立しない。
　「株式時価総額に有利子負債金額を加えたもの」を狭義の意味での企業価値(ここではEnterprise Value)と呼び、上記の意味での企業価値の代替値として用いる場合もある。

4.1　企業価値創造を目指すべき背景

　日本企業は、外部環境の変化を受け、企業価値創造の面で相対的に海外企業に劣後していると言われる。

(1)	会計制度の改革	会計制度改革やIFRSの影響の結果、企業価値評価や公正価値評価が必要となり、市場変動や為替変動に関するリスク管理が従前以上に必要となった。
(2)	所有構造の変化	バブル崩壊以後、持ち合い株の解消や外国人投資家の参入の結果、企業価値に対する感度が高い主体が株式を保有。
(3)	M&Aの増加	少子高齢化・長期的なデフレーション、市場のボーダーレス化の結果、国内市場の縮小・海外市場の進出が必然となり、成長施策の一案として、M&Aが身近になった。
(4)	現金保有高の増加	有利子負債額を超える額の現預金を保有している「実質無借金会社」が増加しているが、投資家からすれば、設備投資か配当・自社株買いによる還元を求めるはずであり、経営者は適切な対応が求められる。
(5)	非財務情報の開示	資本市場や経営者の短期(経営)志向を回避し、持続的成長を促すための方策として、非財務情報の開示に注目が集まっている。

4.2　日本M&A市場の推移

　日本M&A市場は、バブル期以降、拡大している。

図表4　日本M&A市場の規模(左：1985年以降のマーケット別M&A件数の推移、右：1985年以降のマーケット別M&A金額の推移)

出典：MARR Online*10

4.3　企業価値評価の観点

　企業価値創造を目標とするためには、まず企業価値の評価方法を学ぶ必要がある。企業価値評価に当たっては、

経営
財務
経営戦略

の3点から総合的かつ高度な分析を行う必要がある。
　企業は、以下の一連の活動を繰り返して成長していく。

債権者・株主より資金を調達する。
調達資金で資源(インプット)を購入、製品・サービス(アウトプット)を提供し、利益を得る。
利益から債権者・株主に還元し、残存利益を企業が受取る。

4.4　資金調達と企業

企業と債権者・株主の関係は、財務諸表との関係で概容をつかむことができる。

5.　企業価値評価

　企業価値の測定に当たっては、以下の3概念を理解する必要がある。

キャッシュフロー
時間価値(現在価値)
資本コスト

　企業価値算出に当たっては、フリー・キャッシュフローをWACC(後述)で割引くことで企業価値を算出することが多い。

5.1　企業価値評価の事例

　初期投資として $30$ 億円を要求し、2年目から $10$ 年間、確定的に $7$ 億円のキャッシュ・インフローを発生させる投資プロジェクトを考える。資金提供者である銀行が $5\%$ の利息を要求する場合、当該プロジェクトの価値はいくらか。

$\begin{aligned} NPV=&-30+\displaystyle{\frac{7}{1.05}}+\cdots+\displaystyle{\frac{7}{1.05^{10}}}\\ =&24.05[億円] \end{aligned}$

5.2　企業価値評価のための財務(ファンダメンタル)分析

　企業価値評価に当たっては、以下の観点から企業の財務評価を行う。

(1)	収益性の分析	過去の成果を評価する。
(2)	効率性の分析	企業が効率的に収益を上げているかを評価する。
(3)	安全性の分析	資金ショートの蓋然性を評価する。
(4)	成長性の分析	企業の将来的な姿を評価する。

最後、以上を総合的に評価する。

5.2.1　企業価値評価におけるROE

　企業価値評価において、最も汎用的な指標は自己資本利益率(ROE)である：

$\begin{aligned} 自己資本利益率=&\displaystyle{\frac{当期純利益}{自己資本}}\times 100 [\%]\\ =&\displaystyle{\frac{当期純利益}{株主資本+その他の包括利益累計額}}\times 100 [\%]\\ \end{aligned}$

なぜならばROEが株価と連関性をもつためである。株価は以下のように分解できる。

$\begin{aligned} 株価=PER\times EPS=\displaystyle{\frac{株価}{1株当たり純利益}\times\frac{当期純利益}{期中平均発行済普通株式数}} \end{aligned}$

　ここに、以下を代入する。

$\begin{aligned} EPS=\displaystyle{\frac{自己資本}{期中平均発行済普通株式数}\times\frac{当期純利益}{自己資本}} \end{aligned}$

　以上から、株価はPER、EPS、BPSを介してROEと連関性を持つことが分かる。

$\begin{aligned} &株価=\displaystyle{\frac{株価}{1株当たり純利益}\times \frac{自己資本}{期中平均発行済普通株式数}\times \frac{当期純利益}{自己資本}}\\ \therefore\ &株価=PER \times BPS \times ROE \end{aligned}$

　また、過去回で紹介済だが、ROEはROAと財務レバレッジに分解できる。つまり利益が少なくとも、レバレッジを掛けることでROEを向上させることができる。

$\begin{aligned} ROE=&\displaystyle{\frac{当期純利益}{自己資本}}=\displaystyle{\frac{当期純利益}{総資産}}\times \displaystyle{\frac{総資産}{自己資本}}\\ =&ROA \times 財務レバレッジ\\ =&\displaystyle{\frac{当期純利益}{売上高}}\times\displaystyle{\frac{売上高}{総資産}}\times 財務レバレッジ \end{aligned}$

　ここで導入したROAは、分母の総資産に株主と債権者が拠出した資産の合計であるが、分子は、支払利息控除済の当期純利益を用いており、評価に当たり齟齬を生じている。

$\begin{aligned} ROA =\displaystyle{\frac{当期純利益}{総資産}}\times100 \end{aligned}$

　そこで、収益性の分析に当たっては、代替として(総資本事業利益率)を用いる場合がある。

$\begin{aligned} ROI=\displaystyle{\frac{事業利益}{総資産}}\times100 \end{aligned}$

5.2.2　企業価値評価における効率性分析

　総資産回転率は、資産活用の効率性を測っている。

$\begin{aligned} 総資産回転率=&\displaystyle{\frac{売上高}{総資産}} \end{aligned}$

実務では、個々の資産が適切に活用されているのかを測るため、様々な指標を用いる。

$\begin{aligned} 有形固定資産回転率=&\displaystyle{\frac{売上高}{有形固定資産}},\\ 棚卸資産回転率=&\displaystyle{\frac{売上高}{棚卸資産}},\\ 売上債権回転率=&\displaystyle{\frac{売上高}{売掛金+受取手形+割引手形}},\\ 仕入債務回転率=&\displaystyle{\frac{売上高}{買掛金+支払手形}} \end{aligned}$

　回転日数を総合した指標として、CCC(Cash Conversion Cycle)がある。

$\begin{aligned} CCC=棚卸資産回転期間+売上債権回転期間-仕入債務回転期間 \end{aligned}$

　また、手元流動性の判断基準として、手元流動性比率を利用する。以下では月商を用いる。

$\begin{aligned} 手元流動性比率=\displaystyle{\frac{現金預金+短期性有価証券}{売上高/12}} \end{aligned}$

5.2.3　キャッシュフロー分析

　企業が、どの程度の現(預)金を稼ぎ、投資し、借金を返済しているのかを理解するためにキャッシュフローを見る。
そこで、

(1)	営業キャッシュフロー	営業活動によって現金流入があるかどうか？
(2)	投資キャッシュフロー	投資活動によって現金が流出しているか？
(3)	財務キャッシュフロー	財務活動(借入・返済)によって現金が流出しているか？

のうち、特に(1)、(2)を見る。
　キャッシュフローを分析するには、各々の符号だけでもいくつかわかることがある。

図表5　キリンホールディングスのキャッシュフローの推移

　キャッシュフロー分析においては、フリー・キャッシュフロー(FCF)も重視される。これは、資本提供者(株主・債権者)に分配・提供可能なキャッシュを意味する。具体的には、営業CFから経常的な活動に必要なキャッシュ・アウトを差し引いたものとして定義する(簡便的には営業CFから投資CFを差し引く)。

$\begin{aligned} FCF=&営業CF-経常的な活動に必要なキャッシュ・アウトフロー\\ =&NOPAT(=営業利益\times(1-正味法人税率) )+当期減価償却費\\&-設備投資費-正味運転資本増加額\\ \approx&営業CF-投資CF \end{aligned}$

　経常的な活動に必要なキャッシュ・アウトフローとして、何を用いるかは議論があるが、特段憂慮事項がなければ、投資CFが用いられることが多い。
　また、フリー・キャッシュフローについては、その利用用途にも目を配る必要がある。配当や自社株買いにより株主に還元しているのか、借入債務の返済に充てるのか、内部留保として企業内部に蓄積するのか、といった様々な利用が考えられる。

5.3　グループ経営分析

　通常、ある程度の規模の事業体であれば、子会社等複数の企業を抱えた企業グループを成す場合が多い。このとき、当該事業体の中で主体となる(単体)企業がグループ内でどの程度の地位を占めているかを分析する手法を考える。
　簡単なものとしては、連単倍率がある。ある指標 $X$ について、連結の場合の値と単体の場合の値とを比較する。

$\begin{aligned} 連単倍率=\displaystyle{\frac{X(連結)}{X(単体)}}[倍] \end{aligned}$

但し、持株会社や子(関連)会社を持たない場合、意味をなさない。
　また、グループに焦点を当てるには、セグメント分析がある。セグメントとは、以下の3条件をすべて満たす企業の構成単位を言う。

(1)	収益を獲得し、費用が発生する事業活動。
(2)	企業の最高意思決定機関が意思決定を行なう単位。
(3)	分離された財務情報が入手できる。

通常、セグメント情報は、有価証券報告書上で事業別や地域別に開示されていることが多い。またセグメント情報を用いてセグメント毎の事業価値を計算し、これらを合算することで算出する企業価値算出方法をSum of th Partsという。

5.4　経営戦略分析

　会計情報の分析を通じて、企業の経営戦略・産業特性を分析することもできる。例えばROEの所在国別分布を見ると、日本企業は高水準企業が他国対比で少ないが赤字企業も他国対比で少ないという特徴を持ち、全体として、他国対比で低ROEである。
　この差異は、策定した戦略を好業績に結び付けるだけの実行力がないことが一因であると考えられる。以下の2点が戦略実行力を支えると考えられる。
(1)戦略目標の策定能力
(2)戦略実行の分析・評価能力

5.4.1　企業価値創造のための経営戦略過程

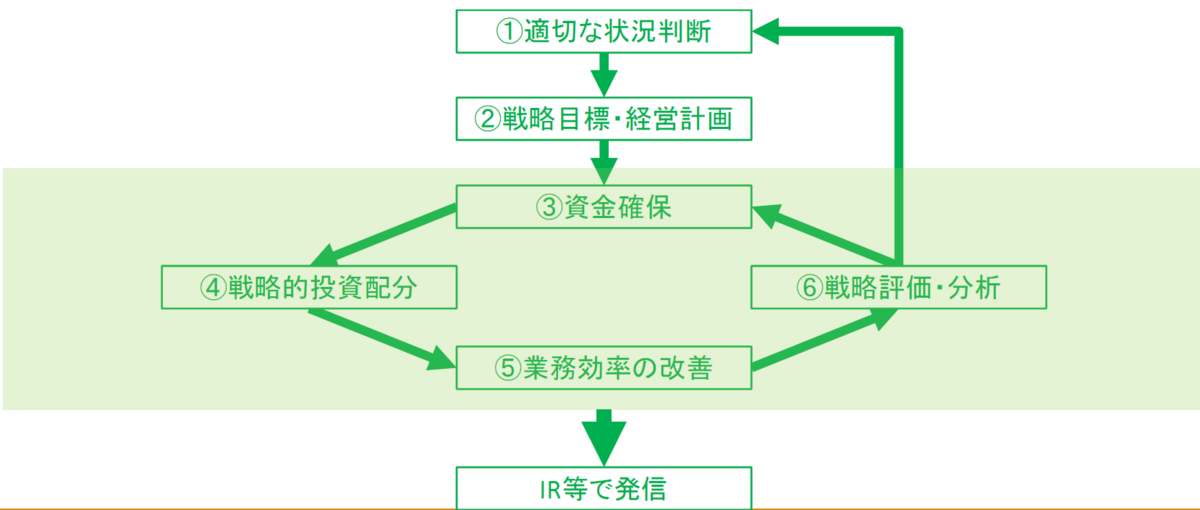
5.4.2　企業価値創造のための経営戦略分析

　企業価値を分析するに当たって考慮すべき経営戦略の分析手法をまとめると以下の4つになる。

分析内容

(1)	業界構造分析	企業が属する、参入する業界の特性分析。	Five Forces Analysis, Market Position Analysis, Value Chain Analysis
(2)	事業構造分析	目標・計画達成のため注力する事業の選定・投資金額の配分・投資成果の分析。	Market Portfolio Analysis
(3)	業務構造分析	業務の効率性の分析。	Turnover Analysis, Break-Even Point Analysis
(4)	資本構造分析	目標・計画達成に最適な資本調達手段の分析。	Finance Leverage Analysis

　これらはROEの分解式において各要素に関係する：

5.4.3　Five Forces Analysis

　Michael Porterが提唱した概念で、企業の競合を整理するためのフレームワークである。

図表6　Five Forces Analysisの概念図

出典：Porter(1980)を基に作成

5.4.3　業界の競争度合いを計測する方法

　業界の競争度合いを計測する指標としてHHI(Herfindahl-Hirschman Index)がある。
　ある市場(業界)における企業(または製品・サービス)のシェアが既知であるとする。ある市場に存在する企業(または製品・サービス) $i$ の市場占有率 *11を $S_i,\ i=1,2,\cdots,n,\ 0\lt S_i\lt1,\ \displaystyle{\sum_{i}^{n}S_i=1}$ とおく。このときHHIを以下で定義する：

$\begin{aligned} HHI=\displaystyle{\sum_{i=1}^{n}{S_i}^2} \end{aligned}$

　HHIは独占状態( $n=1$ )のとき $1$ を取り、また $S_i\gt0$ であるから $0\lt HHI\leq1$ が成り立つ。すなわち、HHIが小さければ小さいほど競争は激しく、逆にHHIが大きければ競争は緩やかであり、競争が無い独占状態であるときにHHIは最大値 $1$ を取る。
　またシミュレーション結果から以下の傾向が分かる：

企業(または製品・サービス)間の市場占有率の差が小さいほど(=突出してシェアを持つ企業(または製品・サービス)が無ければ無いほど)、HHIは小さくなる。
市場に参加する企業(または製品・サービス)数が増えるほど、HHIは小さくなる。

図表7-1　HHIのシミュレーション結果(1)(左=2社の場合,右=3社の場合*12 )

図表7-2　HHIのシミュレーション結果(2)(企業数が変化する場合*13 )

5.4.4　バリューチェーン分析

　各企業の利益率を分析するに当たり、バリューチェーン分析も重要である。すなわち製品・サービスの生産における各過程で付与される付加価値を分析するものである。
　バリューチェーン分析に当たっては、近年、製造(サービス)工程の上流・下流の付加価値が大きい(中流での付加価値が低い)という、スマイルカーブ現象が報告されている。

図表8　バリューチェン分析におけるスマイルカーブ現象のイメージ

5.4.5　事業構造分析とPPM

　事業構造分析の狙いは、戦略目標・経営計画を達成するために注力すべき事業、各事業へ配分する投資金額、投資と成果との関係を分析することにある。
　そもそも多角化を図る目的にはリスク分散がある。実際、セグメント数が増すにつれて利益率のバラツキが小さくなることが知られている。その一方で、セグメント数が増すにつれて利益率水準も小さくなることも確認されている。そこで利益率を優先するならば、セグメント数を適度な水準に保ち、状況によっては撤退をしてセグメント数を減らす必要がある。
　そうした意思決定を踏まえて事業構造分析をするに当たっては、BCGが開発したPPMが使われることがある。PPMは以下の3つの仮定を置いた、資源配分の効率化を目的としたツールである：

相対市場シェアが高い程、キャッシュ創造能力が高い。
所属する市場成長率が高い程、キャッシュ(投資)が多く必要になる。
時間の経過と共に市場成長率は逓減する。

図表9　PPMの模式図*14

　自社のセグメントが所属する市場について、そのセグメントの相対市場シェアと当該市場成長率をプロットし、相対市場シェアの高低・市場成長率の高低に応じて4象限に当てはめる。

　PPMによる分析結果を基にすると、以下の3つの方策を取るべきである：

「負け犬」および「競争力のない問題児」からは撤退し、資金を回収する。
回収資金や金のなる木が生んだ資金は、競争力のある「問題児」に投資して、「花形」へと育成する。
「花形」および「金のなる木」には、市場シェア維持のために一定量の投資。

5.4.6　業務構造分析

　業務構造分析に当たっては、回転率分析が重要となる。何の回転率を分析するかは、業種等によって異なるため、まずはその見極めが課題となる。例えば、製造業であれば、棚卸資産回転率を見ることで、在庫の多さを検討することができる。
　また売上高とそのコストとの関係性を通じた損益を分析する手法として、損益分岐点分析を通じて企業のコスト構造を把握し効率的な経営のための参考情報を得ることができる。
　まずは全ての費用(コスト・原価)を変動費(売上高や販売量に応じ比例して変化する原価)、固定費(売上高や販売量といった営業量とは無関係に固定的に発生する原価)に分類する。すると利益が売上から費用を差し引いたものであるという関係から以下が成り立つ：

$\begin{aligned} 利益=&売上高-費用,\\ 利益=&売上高-(固定費+変動費) \end{aligned}$

　理想的な経営状態では変動費 $=0$ のときに利益が最大化する。すなわち利益はこれを上回ることはない。このときの利益を限界利益といい、限界利益の売上高に対する割合を限界利益率という(対照的に変動費が売上高に占める割合を変動費率という。)。

$\begin{aligned} 限界利益=&売上高-変動費\\ 限界利益率=&\displaystyle{\frac{限界利益}{売上高}}=\displaystyle{\frac{売上高-変動費}{売上高}}=1-変動費率 \end{aligned}$

　次に、利益が $0$ となる、すなわち赤字にならないように最低限確保すべき売上高(損益分岐点売上高)を考えることができる。すなわち、

$\begin{aligned} 売上高=固定費+変動費 \end{aligned}$

が成り立つような売上高を損益分岐点売上高という。
　より具体的に分析する。ある製品の売上について、その販売数を $X$ 、販売数1単位当たりの売上高・変動費をそれぞれ $S,C$ とし、固定費・利益をそれぞれ $F,P$ と書くことにする。通常、費用に利益を上乗せした額で販売すると考えられるから、 $S\gt C$ *15であると仮定でき、このとき

$\begin{aligned} P=S\cdot X-(C\cdot X+F) \end{aligned}$

が成り立つ。したがって限界利益 $P_{m}$ および限界利益率 $r_{m}$ は

$\begin{aligned} P_m=&S-F\\ r_m=&\displaystyle{\frac{S-F}{S}}=1-\displaystyle{\frac{F}{S}} \end{aligned}$

である。
本式で $P=0$ とおいた際に $X$ について解いた解から得られるのが損益分岐点売上高である。すなわち、損益分岐点売上高 $S_0$ は、そのときの $X=X_0$ とすれば、

$\begin{aligned} \ &(S_0-C)X_0-F=0\\ \ & S_0X_0=F+CX_0\\ \therefore\ &\ X_0=\displaystyle{\frac{F}{S_0-C}}=\displaystyle{\frac{\displaystyle{\frac{F}{S_0}}}{\displaystyle{\frac{S_0-C}{S_0}}}}=\displaystyle{\frac{固定費率}{1-変動費率}}\\ \ &S_0=SX_0=\displaystyle{\frac{FS}{S_0-C}}=\displaystyle{\frac{固定費}{1-変動費率}}=\displaystyle{\frac{固定費}{限界利益率}} \end{aligned}$

が成り立つ。
　また、以下の安全性(安全余裕率)を計算することで、経営の安全性を測ることもできる。これは、現在の売上高の何 $\%$ までならば売上が減少しても赤字にならないで済むかを見る指標である。

$\begin{aligned} 安全余裕率=\displaystyle{\frac{実際の売上高− 損益分岐点売上高}{実際の売上高}}\times 100 [\%] \end{aligned}$

　実例を挙げて考えてみる。
　A商店は、商品Bを1単位当たり1,000円で売っている。原価等の変動費は商品B1単位当たり500円かかり、店舗維持として固定的に200万円かかるとする。このとき、店舗売上が赤字にならないためには、少なくとも400万円(4,000単位)を
売上げなければならない。

$\begin{aligned} \ &(0.1万円-0.05万円)X-200万円=0 \therefore\ &\ X=\displaystyle{\frac{200}{0.05}}=4000,\\ \ &\ S_0=0.1X_0=400万円 \end{aligned}$

また6,900単位売上げたときの安全余裕度は

$\begin{aligned} 安全余裕率=\displaystyle{\frac{1000\times 6900−4000000}{1000\times 6900}}\times 100 =42.029[\%] \end{aligned}$

である。
　高い収益を上げるためには、損益分岐点を下げる(損益分岐点売上高を下げる)ことが必要となる。これには、
　(1)固定費を下げる
　(2)変動費を下げる
ことが有効だか、それぞれを変化させた際のインパクトを数値で検証できることが損益分岐点分析の利点である。

5.4.7　資本構造分析

　企業の資金調達状況を分析するために、企業の資本構造を分析する*16。
　ROE分解式を見れば、負債調達をすることで、財務レバレッジを通じてROEを高めることができる。しかし過度に負債調達すれば返済負担が増し安全性が低減する。他方で負債調達による支払利息は税金がかからないため節税効果が得られるのであり、これらにはトレードオフ関係があるため、企業は負債・株式の最適な資本構成を模索することとなる。
　この最適な資本構成では、Modigliani-Millerの定理が有名である。すなわち

Modigliani-Millerの定理(第一命題) $税金や取引に関わる諸経費が存在しない「完全市場」においては、\\資本構成(負債と株主資本の組み合わせ)は企業価値に影響を与えない。$

　法人税を考慮したMMの修正命題では、法人税を考慮すると、レバレッジを掛ける(負債を増やす)と資本コスト(加重平均資本コスト(WACC) 後述)が下落するのため、企業価値向上に寄与することを主張している。このように企業価値向上のための資本構成において、理論的にも適度な負債調達が必要であるが主張されている。
　なお資本構造の最適性は、ビジネスモデルや既存株主属性、当社の信用力・金利水準等、様々な要素が複雑に絡むため、定量分析のみならず、定性面にも留意する必要がある。

次回

power-of-awareness.com

参考文献

砂川伸幸、川北英隆、杉浦秀徳(2008)「日本企業のコーポレートファイナンス」日本経済新聞社
砂川伸幸、川北英隆、杉浦秀徳、佐藤淑子(2013)「日本企業のコーポレートファイナンス」日本経済新聞社
Brealey, Myers, Allen (2014), ”Principles of Corporate Finance, Global Edition,“ McGraw Hill
伊藤邦雄(2014)「新・企業価値評価」日本経済新聞出版社
Porter M. (1980), “Competitive Strategy,” Free Press
代田豊一郎／馬場直彦(2002)「リアル・オプションの基本原理と経済学への応用について―不確実性下の意思決定モデル―」金融研究(http://www.imes.boj.or.jp/research/papers/japanese/kk21-2-9.pdf)

*1:このディスカウント・ファクターを具体的に計算するときには、割引に用いる金利(割引金利という)として何を用いるかが焦点の1つになる。リスク・フリー・レートにその評価対象のリスクに見合ったプレミアムを乗せた金利を用いるなどが考えられるが、これについては後述する。

*2:そのまま利用するのはデフォルトの無い債券の評価に用いるのみであり、実際には評価対象となるもののリスクに見合ったプレミアムをスポット・レートに上乗せしたものを割引金利として用いる。

*3:理論的には現時点でスタートするという意味。

*4:完全に無リスクで期中のクーポン支払いの無い債券)))に内在する金利((内在する金利とは将来時点のキャッシュフローの現在価値と現在時点のキャッシュフローの金額を等しくする割引金利を意味する。

*5:課題は、日本の場合、ゼロクーポン債が2ヶ月、3ヶ月、6ヶ月、1年物しかない点である。

*6:日本の場合、国庫短期証券が相当する。なお満期が1年以上の債券と国庫短期証券は逆イールド(年限が短い債券の金利の方が高くなる現象。)が実証的に起こりがちで、評価における重要性に応じてこれを良しとするか考えるべきである。たとえば数年～数十年スパンのキャッシュフローを評価し、短期のキャッシュフロー金額が相対的に小さいのであればその重要性は低いから無視しても良いということになる。

*7:簡便的には線形補間だが、デリバティブの評価などである程度の正確性などが求められるのであれば、スプライン補間(3次スプラインが良く用いられる)を行なう。

*8:スポット・レートは現時点から始まる金利であるが、これに対して将来時点から始まるをフォワード・レートといい。その時間に対する微小変化を瞬間フォワード・レートという。

*9:企業がデフォルトせず永続すること。

*10:https://www.marr.jp/genre/graphdemiru参照。

*11:何を用いて市場占有率を計算するかは議論の余地が大きい。売上高を使うことも考えられるし、たとえば自動車であれば新車販売台数を使うなど、個々の問題に応じて適当なものを思案する必要がある。

*12:3社の場合において、 $y=1-x$ よりも右上(厳密には $\{(x,y)|0\leq x\leq1,0\leq y\leq1,y\geq1-x\}$ )ではHHIが定義できない点に注意。

*13:シェアは全社同一とした。

*14:各セグメントの売上高(ないし利益額)を本図のようにプロットの大きさで表す場合がある。

*15:後に $分母=0$ となることを避けるための便宜的なものであるので、実際には採算割れ $S\lt C$ もあり得る。 $S\neq C$ でない限り、以降の議論が成り立つ。

*16:ここでいう資本は企業に拠出された資本の意味で、会計用語でいう資産を指す。

1. 金利の確認

1.1 金利とは何か

1.2 金利の計算方法

1.3 リスク・フリー・レート

2. コーポレート・ファイナンスとは

2.1 コーポレート・ファイナンスの基本的概念

2.2 コーポレート・ファイナンスの焦点

3. DCF法

3.1 現在価値

3.2 ディスカウント・ファクター

3.3 NPV

3.4 割引に利用する利回り

3.4.1 スポット・レートの算出例(1) 国債を利用する方法

3.4.2 スポット・レートの算出例(2) スワップ・レートを利用する方法

3.4.3 スポット・レートの算出例(3) 金利モデルを利用する方法

3.4.4 現在価値の算出事例(1) コンソル債

3.4.5 現在価値の算出事例(2) 定率成長

3.5 回収期間と内部収益率

3.5.1 回収期間

3.5.2 内部収益率

4. 企業価値評価：ファンダメンタル手法

4.1 企業価値創造を目指すべき背景

4.2 日本M&A市場の推移

4.3 企業価値評価の観点

4.4 資金調達と企業

5. 企業価値評価

5.1 企業価値評価の事例

5.2 企業価値評価のための財務(ファンダメンタル)分析

5.2.1 企業価値評価におけるROE

5.2.2 企業価値評価における効率性分析

5.2.3 キャッシュフロー分析

5.3 グループ経営分析

5.4 経営戦略分析

5.4.1 企業価値創造のための経営戦略過程

5.4.2 企業価値創造のための経営戦略分析

5.4.3 Five Forces Analysis

5.4.3 業界の競争度合いを計測する方法

5.4.4 バリューチェーン分析

5.4.5 事業構造分析とPPM

5.4.6 業務構造分析

5.4.7 資本構造分析

次回