ファイナンス練習(2021年09月16日) - 「大人の教養・知識・気付き」を伸ばすブログ

　業務でC#を用いることになったので、最近勉強していなくて朧気になってきた知識をReviseする意味でも、以下の書籍を読みながらC#で実装してみる。今回はP.214-222まで。

EXCEL&VBAで学ぶファイナンスの数理

Amazon

8. 金融工学の基礎

8. 金融工学の基礎

　最後となる本章では、デリバティブの価格付け理論を取り扱う。価格付け理論の根本原理は「同一のキャッシュフローを生成する金融資産の現在価値は等しい」という一物一価の法則である。これを正当化するために、更に

コスト無しに無リスクで利益を上げられる投資機会を裁定機会という。

という概念を定義した上で、無裁定であることをかていする。

8.1 二項モデルによるオプション評価

8.1.1 1期間モデル

　行使価格 $K$ のコール・オプションを評価する。原資産価格が1期間後に確率 $p$ で上昇、確率 $1-p$ で下落するとする。また各パラメータを以下の設定どおりとする：

現時点における原資産の市場価格： $S$
1期間後において確率 $p$ で発生する上昇局面での上昇率： $u\gt1$
1期間後において確率 $1-p$ で発生する下落局面での上昇率： $d\lt1$
無リスク金利 $r-1$

また

$\begin{aligned} d\lt1\lt r\lt u \end{aligned}$

を条件として課す。
　さてここからデリバティブの価格付けを行うに当たり、複製の概念を定義する：

　任意の資産 $X$ のキャッシュフローとポートフォリオ $Y$ のキャッシュフローが完全に一致するとき、ポートフォリオ $Y$ は資産 $X$ を複製するといい、このときポートフォリオ $Y$ を複製ポートフォリオという。

この議論では、ポートフォリオ $Y$ として原資産と無リスク資産を適当な数量（原資産の保有数： $x$ , 無リスク資産の保有額： $B$ とする）で保有することによって価格評価対象となる資産（オプション）を複製する。
　複製するためには、上昇・下落局面での資産価格をそれぞれ $C_u,\ C_d$ として1期間後のペイオフに関し

${\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} uSx+rB&=C_u,\\ dSx+rB&=C_d \end{array} \right. \end{eqnarray} }$

が成立しなければならない。これを解くことで

$\begin{aligned} x=\displaystyle{\frac{C_u-C_d}{(u-d)S}},\ B=\displaystyle{\frac{uC_d-dC_u}{(u-d)r}} \end{aligned}$

が得られる*1。
　以上から、ポートフォリオの現在価値が資産の現在価値となるから、資産の価格 $C(0)$ は

$\begin{aligned} C(0)=xS+B=\displaystyle{\frac{C_u-C_d}{u-d}}+\displaystyle{\frac{uC_d-dC_u}{(u-d)r}} \end{aligned}$

である。
　オプションの期待収益率は原資産の期待収益率に比べ大きくなりがちである。これは、オプションの場合、自分の想定していない局面に原資産価格が遷移した場合*2でも、オプションの権利放棄（＝オプション価格分の損失）により損失の下限が設定されているからである*3。
　一般に原資産とその上に書かれたデリバティブの単位リスク当たり超過収益率

$\begin{aligned} \displaystyle{\frac{\mu-r}{\sigma}} \end{aligned}$

は一致する。原資産の単位リスク当たり超過収益率をリスクの市場価格*4という。

　原資産とその上に書かれたデリバティブの単位リスク当たり超過収益率は一致するものの、一般に期待収益率は一致しない。これはすなわち原資産のリスクとデリバティブのリスクが、単位リスク当たり超過収益率が一致するような値になっている＝リスクも一般に一致しないことを意味する。これはまた、この相違するリスク分に対してリスク・プレミアムが要求されることを意味する。すなわちリスクが調整されることで複製が可能になっている。
　これに対して、リスクを調整するのではなく、（上昇・下落の）確率を調整することで複製を可能にすることを考えるのも可能である。このようにリスクを確率で調整する、すなわちリスク中立な確率を用いることをリスク中立化法という。このリスク中立な確率は、具体的には、原資産の期待現在価値が現在の価格に一致するように確率を定めればよい（数学ではこの状態をマルチンゲールという。）。この時の確率をマルチンゲール確率という。

8.2. 一般的な二項モデル

　ここまでは1期間としてきたが、これは多期間にすることを考える。つまり、行使価格 $K$ のコール・オプションを評価する問題に対し、原資産価格が翌期間に確率 $p$ で上昇、確率 $1-p$ で下落するとし、

現時点における原資産の市場価格： $S$
翌期間において確率 $p$ で発生する上昇局面での上昇率：時点にかかわらず $u\gt1$
翌期間後において確率 $1-p$ で発生する下落局面での上昇率：時点にかかわらず $d\lt1$
無リスク金利 $r-1$ ：時点にかかわらず一定

とする。
　このような問題設定では、将来時点における原資産価格は複数パターン存在する。 $n$ 時点における下から $(i-1)$ 番目*5のノードを $(n,i)$ とし、このノードにおける株価を $S(n,i)$ 、オプション価格を $C(n,i)$ とする。このとき

$\begin{aligned} S(n,i)=Su^{i}d^{n-i}, i=1,\ 2,\cdots,n,\ n=1,\ 2,\cdots,\ T,\ S(0,0)=S \end{aligned}$

である。
　ノード $(n,i)$ における原資産価格の変動を考えると、

${\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} S(n+1,i+1)&=uS(n.i),\\ S(n+1,i)&=dS(n.i) \end{array} \right. \end{eqnarray} }$

が成り立つ。
　コール・オプション価格は1期間モデルと同様に複製を考えると、

$\begin{aligned} x=\displaystyle{\frac{C(n+1,i+1)-C(n+1,i)}{(u-d)S(n,i)}},\ B=\displaystyle{\frac{uC(n+1,i)-dC(n+1,i)}{(u-d)r}} \end{aligned}$

が得られ、その結果、

$\begin{aligned} C(n,i)=xS(n,i)+B=\displaystyle{\frac{C(n+1,i+1)-C(n+1,i)}{u-d}}+\displaystyle{\frac{uC(n+1,i)-dC(n+1,i)}{(u-d)r}} \end{aligned}$

である。さて満期におけるコール・オプションのペイオフ関数は、

$\begin{aligned} C(T,i)=\max\{S(T,i)-K,0\}=\max\{Su^{i}d^{T-i}-K,0\} \end{aligned}$

が成立する。以上から、満期 $T$ から $C(n+1,i+1)$ および $C(n+1,i)$ から $C(n,i)$ を計算する形で遡っていくことでオプション価格 $C(0,0)$ を計算できる。

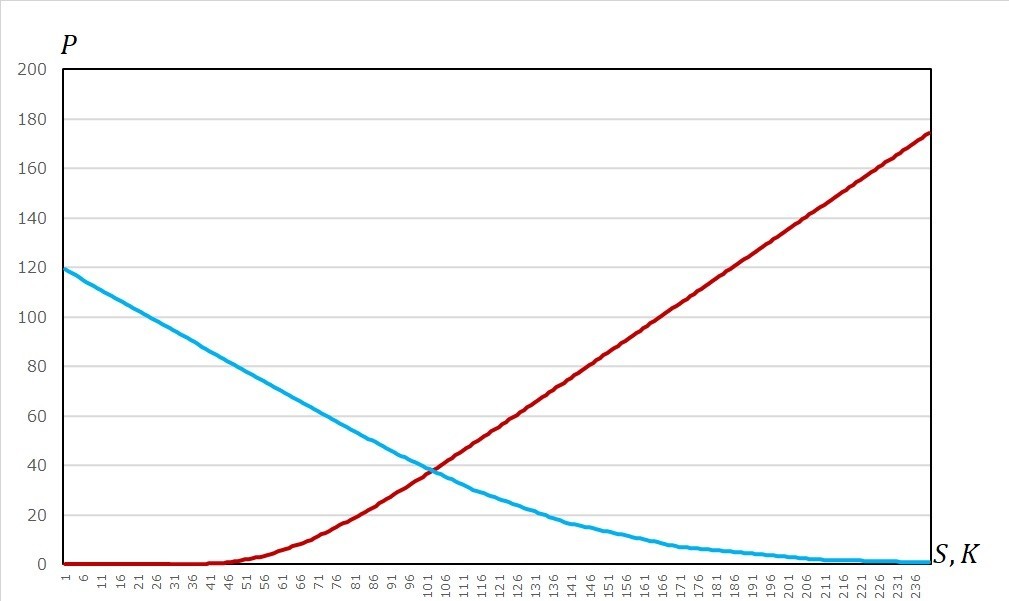
8.3. C#による実装

/// <summary>
/// 2つの値のうち大きい方を取得する
/// </summary>
/// <param name="x">一方の値</param>
/// <param name="y">もう一方の値</param>
/// <returns>max{x,y}</returns>
private static double max(double x, double y)
{
    double z = x + y;
    z += Math.Abs(x - y);
    return 0.5 * z;
}

/// <summary>
/// 多期間二項モデルによるコール・オプション価格評価モデル
/// </summary>
/// <param name="S0">初期時点t=0における原資産価格</param>
/// <param name="K">行使価格</param>
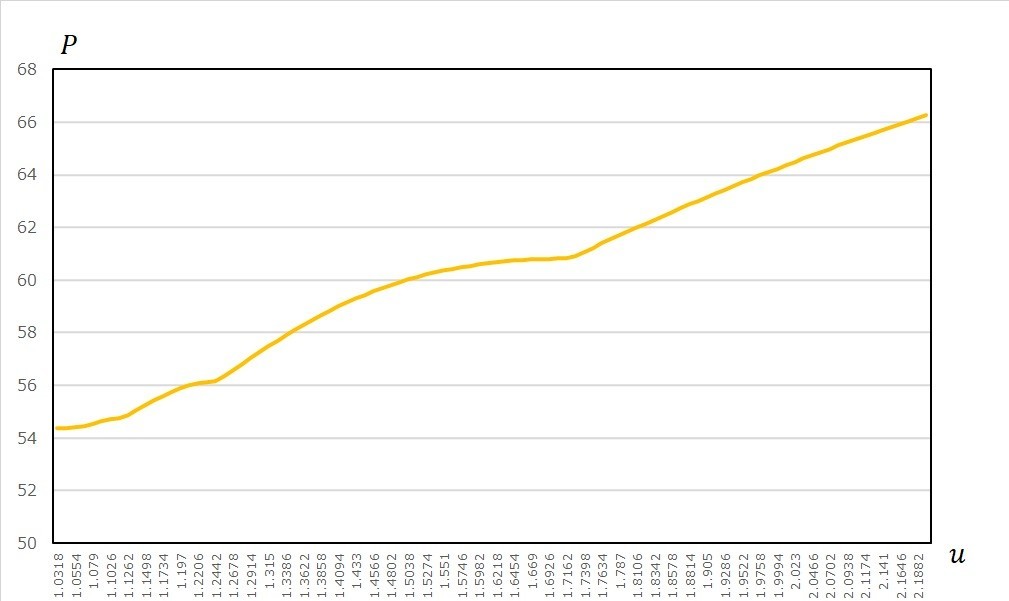
/// <param name="u">上昇率</param>
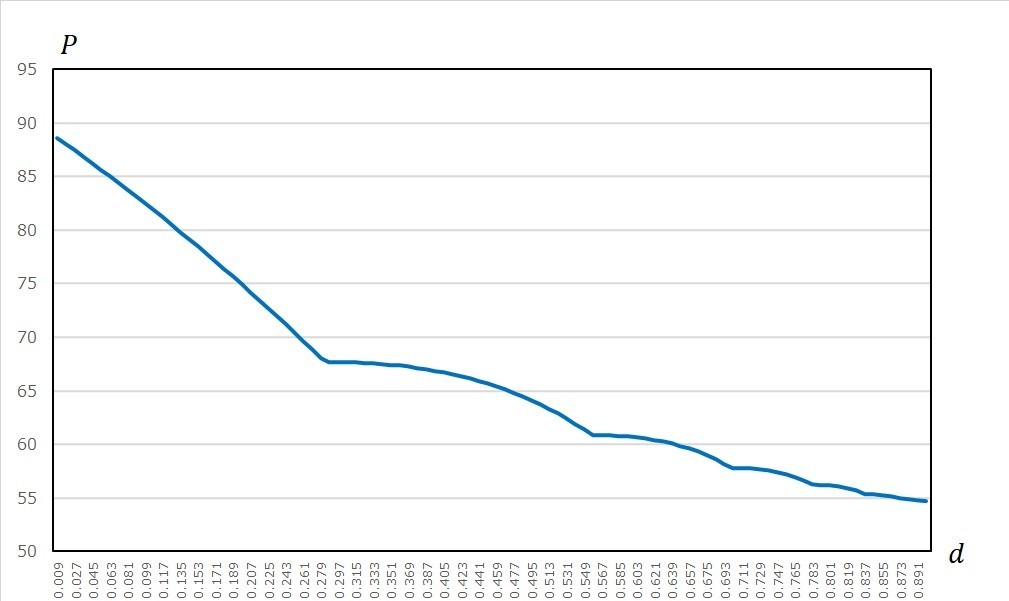
/// <param name="d">下落率</param>
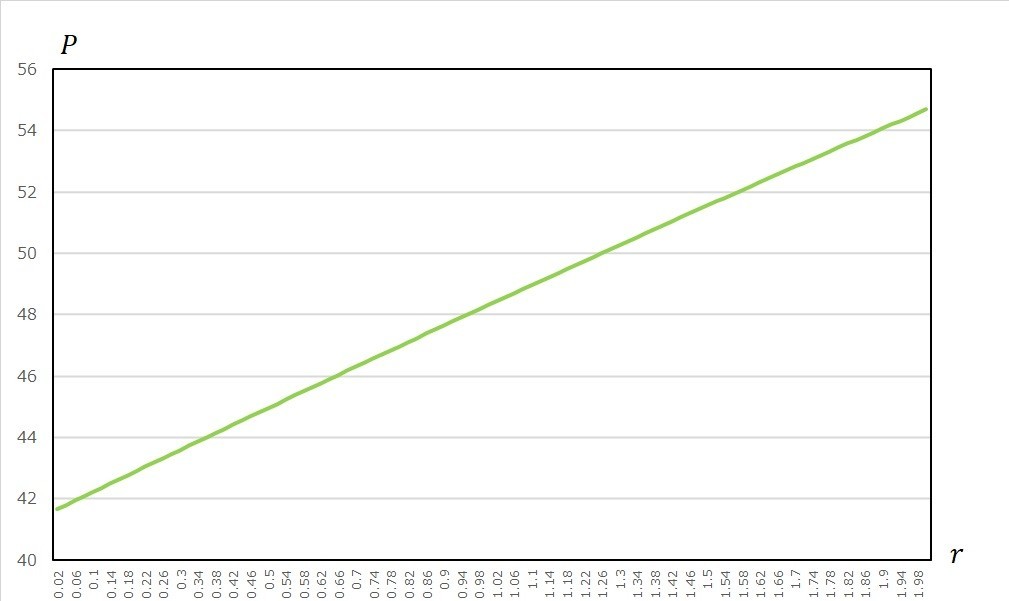
/// <param name="r">無リスク金利</param>
/// <param name="T">満期時点数</param>
/// <returns>初期時点におけるコール・オプション価格</returns>
public static double MultiPeriodBinomialModel(double S0, double K, double u, double d, double r, int T)
{
    // エラーハンドリング①
    if (S0 <=0)
    {
        Console.WriteLine("原資産価格S0が0以下です。0よりも大きい値を入力して下さい。");
        return 0;
    }
    if (K <= 0)
    {
        Console.WriteLine("行使価格Kが0以下です。0よりも大きい値を入力して下さい。");
        return 0;
    }
    if (T<=0)
    {
        Console.WriteLine("満期までの時点数Tが0以下です。1以上を入力して下さい。");
        return 0;
    }

    // エラーハンドリング②：無裁定条件
    if (d>=1)
    {
        Console.WriteLine("下落率が1以上です。1未満の値を入力して下さい。");
        return 0;
    }
    if (r <= 0)
    {
        Console.WriteLine("無リスク金利は正の値のみ受け付けます。");
        return 0;
    }
    if (1 + r >=u)
    {
        Console.WriteLine("上昇率は(1+無リスク金利r)以上でなければなりません。");
        return 0;
    }

    // 各ノード(時点i×上昇数j)のオプション（ペイオフ）価格
    double[,] OptionPrices = new double[T + 1, T + 1]; 

    double OptionPrice = 0.0; //各ノードのオプション価格を一時的に格納
    double OptionPrice_1 = 0.0; //満期でない時点の各ノードのオプション価格第1項部分
    double OptionPrice_2 = 0.0; //満期でない時点の各ノードのオプション価格第2項部分

    // 満期からオプション価格評価
    for (int i = T; i >= 0; i--) // 時点
    {
        for (int j = i; j >= 0; j--) // i時点における各ノードを表す
        {
            // 満期時点の場合はペイオフを評価
            if (i == T)
            {
                OptionPrice = S0 * Math.Pow(u, j) * Math.Pow(d, i - j);
                OptionPrice = max(OptionPrice - K, 0.0);
            }
            else
            {
                OptionPrice_1 = OptionPrices[i + 1, j + 1] - OptionPrices[i + 1, j];
                OptionPrice_1 /= u - d;

                OptionPrice_2 = u * OptionPrices[i + 1, j] - d * OptionPrices[i + 1, j + 1];
                OptionPrice_2 /= (u - d) * (1 + r);

                OptionPrice = OptionPrice_1 + OptionPrice_2;
            }

            OptionPrices[i, j] = OptionPrice;

            OptionPrice = 0.0; //初期化
            OptionPrice_1 = 0.0; //初期化
            OptionPrice_2 = 0.0; //初期化
        }
    }

    return OptionPrices[0, 0];
}

8.4 シミュレーション結果

　基本的なパラメータ値は以下の通りである：

入力パラメータ	概要
初期時点の株価 $S_0$	： $120$
行使価格 $K$	： $80$
上昇率 $u$	： $1.1$
下落率 $d$	： $0.9$
無リスク金利 $r$	： $2\%$
満期までの時点数 $T$	： $10$ 時点

図表1-1　原資産価格 $S$ および行使価格 $K$ を $1$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210916054803j:plain

図表1-2　上昇率 $u$ を動かしたときのオプション価格推移
f:id:suguru_125:20210916054811j:plain

図表1-3　下落率 $d$ を動かしたときのオプション価格推移
f:id:suguru_125:20210916054821j:plain

図表1-4　無リスク金利 $r$ を動かしたときのオプション価格推移
f:id:suguru_125:20210916054829j:plain

図表1-5　満期までの時点数 $T$ を動かしたときのオプション価格推移
f:id:suguru_125:20210916054837j:plain

*1: $u,\ d,\ r$ に課した条件は上式が意味を持つために課したものである。

*2:コール・オプションであれば下落、プット・オプションであれば上昇を指す。

*3:この損失はオプションの売り手が受け持っている。すなわちオプションは買い手が一定以上の損失＝リスクを売り手に転嫁することで買い手は損失によるリスクを限定化し売り手はオプションの売値分を利益として得る代わりに損失が生じた場合には引き受けるというリスクの転移を可能にする金融商品である。この意味でオプションはリスクを取引しているのであり、オプション価格はこのリスクを定量化・可視化していると言えるのである。

*4:CAPMでの議論（https://power-of-awareness.com/entry/2021/09/06/050000）で導入済みである。

*5:下落が $n-i+1$ 回起こったという株価になったということである。