ファイナンス練習(2021年09月15日) - 「大人の教養・知識・気付き」を伸ばすブログ

　業務でC#を用いることになったので、最近勉強していなくて朧気になってきた知識をReviseする意味でも、以下の書籍を読みながらC#で実装してみる。今回はP.206-211まで。

EXCEL&VBAで学ぶファイナンスの数理

Amazon

7. Monte Carloシミュレーション

7. Monte Carloシミュレーション

7.6 満期のペイオフが従う分布が未知なオプション評価

　株価 $S(t)$ が幾何ブラウン運動

$\begin{aligned} dS(t)=rS(t)dt + \sigma S(t)dz(t) \end{aligned}$

に従うと仮定する。ここで $r$ ハムリスク金利、 $\sigma$ はボラティリティ、 $z(t)$ はブラウン運動を表す。
　 $\varepsilon\sim N(0,1)$ として、これを離散化すると

$\begin{aligned} \Delta S(t)=rS(t)\Delta t + \sigma S(t)\varepsilon \sqrt{\Delta t} \end{aligned}$

である。ここで現時点を $0$ 、満期時点を $T$ 、離散化のための分割数を $N$ とすれば、

$\begin{aligned} \Delta t&=T/N\\ \Delta S(t)&=S(t+\Delta t)-S(t)\\ dz(t)&=\varepsilon\sqrt{\Delta t} \end{aligned}$

である。以上から $t=i\Delta t, S_i=S(i\Delta t)\approx S(t)$ として

$\begin{aligned} S_{i+1}=(1+r\Delta t)S_i+\sigma S_i\varepsilon \sqrt{\Delta t},\ i=1,2,\cdots,N-1 \end{aligned}$

が成り立つ。
　この離散化過程を前提とすれば、時点数 $N$ 個分の標準正規乱数を生成すれば、満期時点の株価のシミュレーション値を1つ生成できる。これを多数計算することで、満期時点の株価の分布を生成できる。オプションの文脈で言えば、同様に満期時点の株価のシミュレーション値を1つ生成できるとペイオフ関数を計算でき、その結果としてオプション価格のシミュレーション値が1つ得られる。これを多数繰り返して得た複数のシミュレーション値の平均値を取ることで、得たい期待値（のシミュレーションでの近似値）が得られる。

7.6.1 ルックバック型最大値オプション

　株価 $S(1),S(2),\cdots,S(T)$ のうち最大のもの $\displaystyle{\max_{1\leq t\leq T}\left[S(t)\right]}$ を対象にペイオフを決定する。したがってこのオプションのペイオフ関数 $c_{T}^{(i)}$ は

$\begin{aligned} c_{T}^{(i)}=\max\left[\max_{1\leq t\leq T}\left[S(t)\right]-K,0 \right] \end{aligned}$

である。

7.6.2 ルックバック型平均オプション

　株価 $S(1),S(2),\cdots,S(T)$ の平均 $\bar{S}(T)=\displaystyle{\frac{1}{T+1}}\sum_{t=0}^{T}S(t)$ を対象にペイオフを決定する。したがってこのオプションのペイオフ関数 $c_{T}^{(i)}$ は

$\begin{aligned} c_{T}^{(i)}=\max\left[\bar{S}(T)-K,0 \right] \end{aligned}$

である。

7.6.3 ルックバック型デイ・カウント・オプション

　株価 $S(1),S(2),\cdots,S(T)$ に対し、それらがある基準株価 $\hat{S}$ 以上になった日数が $a$ 以上であった場合に、それらの株価の平均値を対象とするオプションである。すなわち

$\begin{aligned} c_{T}^{(i)}&=\max\left[\left[\displaystyle{\displaystyle{\frac{\sum_{t=1}^{T}S_{t}^{(i)}\cdot \boldsymbol{1}_{\left\{S_{t}^{(i)}\geq \hat{S} \right\}}(S_{t}^{(i)})}{b}}}\right]\cdot\boldsymbol{1}_{\left\{b\geq a \right\}}(b)-K,0\right],\\ b&=\displaystyle{\sum_{t=1}^{T}\boldsymbol{1}_{\left\{S_{t}^{(i)}\geq \hat{S} \right\}}(S_{t}^{(i)})} \end{aligned}$

である。ここで集合 $S$ に対して

${\displaystyle \begin{eqnarray} \boldsymbol{1}_{S}(x)= \left\{ \begin{array}{l} 1, x\in S\\ 0, x\notin S \end{array} \right. \end{eqnarray} }$

と定義する。

7.7 Monte Carlo法のまとめ

　Monte Carloシミュレーションによる価格評価では、原資産の現在価格から将来価格を計算し、発生したそれぞれの経路について価格評価しその平均値を取るという過程を辿る。アメリカン・オプションの場合、各時点で行使可能であるためにより多くのシミュレーション数が必要になるため、様々な工夫がなされる。たとえば準乱数列（ある一様性の基準を満たす確定的な点列）を用いてより効率的な数値積分を行なう。

7.8 C#による実装

7.8.1 準備

　本筋には関係しないもの、内部で参照するメソッドをここで実装しておく。具体的には、

2値のうち大きい方を返すメソッド
株価系列を返すメソッド

の2つを実装する。

using System;
using MathNet.Numerics;

/// <summary>
/// 2つの値のうち大きい方を取得する
/// </summary>
/// <param name="x">一方の値</param>
/// <param name="y">もう一方の値</param>
/// <returns>max{x,y}</returns>

private static double max(double x, double y)
{
    double z = x + y;
    z += Math.Abs(x - y);
    return 0.5 * z;
}

/// <summary>
/// 初期時点から満期までの株価終値の系列を与える
/// </summary>
/// <param name="S0">初期時点の株価。</param>
/// <param name="r">無リスク金利。</param>
/// <param name="std">株価の年次ボラティリティ。0より大きいこと。</param>
/// <param name="T">満期までの日数。1日以上であること。</param>
/// <returns>株価のシミュレーション値</returns>
public static List<double> SimStockPricePath(double S0,double r, double std, int T)
{
    var Ret = new List<double>();

    if (std <= 0)
    {
        Console.WriteLine("ボラティリティが0以下です。0より大きい値を入力して下さい。");
        Ret.Add(-99999.0);

        return Ret;
    }

    if (T < 1)
    {
        Console.WriteLine("日数Tが1未満です。1以上を入力して下さい。");
        Ret.Add(-99999.0);

        return Ret;
    }

    // リターンのパラメータを日次に変換
    double r_d = r / T;
    double std_d = std / Math.Sqrt(T);

    var Random = new MathNet.Numerics.Random.MersenneTwister();

    double StockPrice = 0.0;

    // 初期時点を格納
    Ret.Add(S0);

    //　翌時点t=1から満期t=Tまで
    for (int i =1; i<T; i++)
    {
        StockPrice = (1 + r_d) * Ret[i - 1] + std_d * Ret[i-1] * Random.NextDouble();

        Ret.Add(StockPrice);
    }

    return Ret;
}

7.8.2 ルックバック型最大値オプション

　株価 $S(1),S(2),\cdots,S(T)$ のうち最大のもの $\displaystyle{\max_{1\leq t\leq T}\left[S(t)\right]}$ を対象にペイオフを決定する。したがってこのオプションの価格 $c$ は

$\begin{aligned} c=\displaystyle{\frac{1}{n}\sum_{i=1}^{N}e^{-rT}\max\left[\max_{1\leq t\leq T}\left[S(t)\right]-K,0 \right]} \end{aligned}$

である。

入力パラメータ	概要
初期時点の株価 $S_0$	：初期時点の株価。
行使価格 $K$	：行使価格。
無リスク金利 $r$	：年次無リスク金利。
ボラティリティ $\sigma$	：株価リターンの年次ボラティリティ。
満期までの日数 $T$	：初期時点から満期までの日数。
シミュレーション回数 $N$	：シミュレーションを行う回数。

using System;
using MathNet.Numerics;

/// <summary>
/// ルックバック型最大値コール・オプションの価格を返す
/// </summary>
/// <param name="S0">初期時点の株価。</param>
/// <param name="K">行使価格。</param>
/// <param name="r">無リスク金利。</param>
/// <param name="std">株価の年次ボラティリティ。0より大きいこと。</param>
/// <param name="T">満期までの日数。1日以上であること。</param>
/// <param name="N">シミュレーション数。</param>
/// <returns>ルックバック型最大値コール・オプションの価格</returns>
public static double SimLookBackMaxOption(double S0, double K, double r, double std, int T, int N)
{
    double Ret = 0.0;

    var StockPricePath = new List<double>();

    // エラーハンドリング
    if (K <= 0)
    {
        Console.WriteLine("行使価格Kが0以下です。0以上を入力して下さい。");
        return -99999;
    }

    // 各ペイオフを生成・合成
    for (int i = 0; i<N; i++)
    {
        // 株価系列を取得
        StockPricePath = SimStockPricePath(S0, r, std, T);

        // 最大値を獲得
        StockPricePath.Sort();
        double MaxStockPrice = StockPricePath[StockPricePath.Count - 1];

        double Payoff = max(MaxStockPrice - K, 0);

        Ret += Payoff;
    }

    // 平均化
    Ret /= N;

    // 割引
    double r_d = r / 250;
    Ret *= Math.Exp(-r * T);

    return Ret;
}

7.8.3 ルックバック型平均値オプション

入力パラメータ	概要
初期時点の株価 $S_0$	：初期時点の株価。
行使価格 $K$	：行使価格。
無リスク金利 $r$	：年次無リスク金利。
ボラティリティ $\sigma$	：株価リターンの年次ボラティリティ。
満期までの日数 $T$	：初期時点から満期までの日数。
シミュレーション回数 $N$	：シミュレーションを行う回数。

using System;
using MathNet.Numerics;

/// <summary>
/// ルックバック型アベレージ・コール・オプションの価格を返す
/// </summary>
/// <param name="S0">初期時点の株価。</param>
/// <param name="K">行使価格。</param>
/// <param name="r">無リスク金利。</param>
/// <param name="std">株価の年次ボラティリティ。0より大きいこと。</param>
/// <param name="T">満期までの日数。1日以上であること。</param>
/// <param name="N">シミュレーション数。</param>
/// <returns>ルックバック型アベレージ・コール・オプションの価格</returns>
public static double SimLookBackAverageOption(double S0, double K, double r, double std, int T, int N)
{
    double Ret = 0.0;

    var StockPricePath = new List<double>();

    // エラーハンドリング
    if (K <= 0)
    {
        Console.WriteLine("行使価格Kが0以下です。0以上を入力して下さい。");
        return -99999;
    }

    double AveStockPrice = 0.0;

    // 各ペイオフを生成・合成
    for (int i = 0; i < N; i++)
    {
        // 株価系列を取得
        StockPricePath = SimStockPricePath(S0, r, std, T);

        // 株価系列の平均値を獲得
        foreach(double SP in StockPricePath)
        {
            AveStockPrice += SP;
        }

        AveStockPrice /= T;

        double Payoff = max(AveStockPrice - K, 0);

        Ret += Payoff;
    }

    // 平均化
    Ret /= N;

    // 割引
    double r_d = r / 250;
    Ret *= Math.Exp(-r * T);

    return Ret;
}

7.7.4 ルックバック型デイ・カウント・オプション

入力パラメータ	概要
初期時点の株価 $S_0$	：初期時点の株価。
基準株価 $\bar{S}$	：基準株。
行使価格 $K$	：行使価格。
無リスク金利 $r$	：年次無リスク金利。
ボラティリティ $\sigma$	：株価リターンの年次ボラティリティ。
基準日数 $\bar{c}$	：初期時点から満期までの格株価が基準株価を超えた日数の最低基準。
満期までの日数 $T$	：初期時点から満期までの日数。
シミュレーション回数 $N$	：シミュレーションを行う回数。

using System;
using MathNet.Numerics;

/// <summary>
/// ルックバック型デイ・カウント・コール・オプションの価格を返す
/// </summary>
/// <param name="S0">初期時点の株価。</param>
/// <param name="S_bar">デイ・カウントの基準株価</param>
/// <param name="K">行使価格。</param>
/// <param name="r">無リスク金利。</param>
/// <param name="std">株価の年次ボラティリティ。0より大きいこと。</param>
/// <param name="cnt_bar">基準日数。</param>
/// <param name="T">満期までの日数。1日以上であること。</param>
/// <param name="N">シミュレーション数。</param>
/// <returns>ルックバック型デイ・カウント・コール・オプションの価格</returns>
public static double SimLookBackDayCountOption(double S0,double S_bar, double K, double r, double std,int cnt_bar, int T, int N)
{
    double Ret = 0.0;

    var StockPricePath = new List<double>();

    // エラーハンドリング
    if (K <= 0)
    {
        Console.WriteLine("行使価格Kが0以下です。0以上を入力して下さい。");
        return -99999;
    }
    
    // 各ペイオフを生成・合成
    for (int i = 0; i < N; i++)
    {
        // 株価系列を取得
        StockPricePath = SimStockPricePath(S0, r, std, T);

        int cnt = 0;
        double AveStockPrice = 0.0;

        // 株価系列の平均値を獲得
        foreach (double SP in StockPricePath)
        {
            if(SP >= S_bar)
            {
                cnt += 1;
                AveStockPrice += max(SP - S_bar, 0.0);
            }
        }

        // 1日も基準株価に到達しなかった経路の場合で場合分け
        if (cnt > 0)
        {
            AveStockPrice /= cnt;

            double Payoff = max(AveStockPrice - K, 0);

            if (cnt >= cnt_bar)
            {
                Ret += Payoff;
            }
        }
    }

    // 平均化
    Ret /= N;

    // 割引
    double r_d = r / 250;
    Ret *= Math.Exp(-r * T);

    return Ret;
}

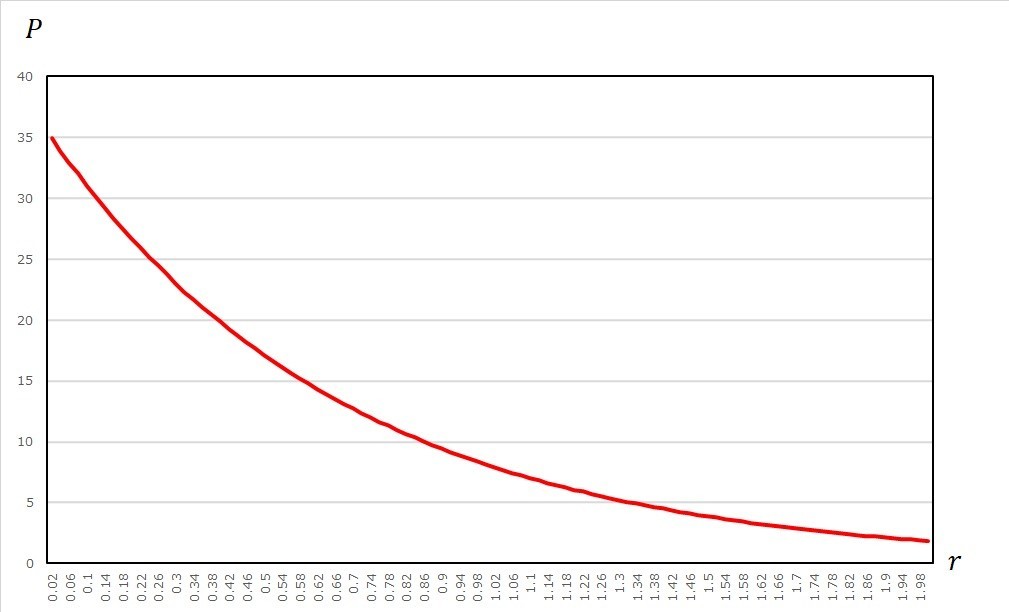
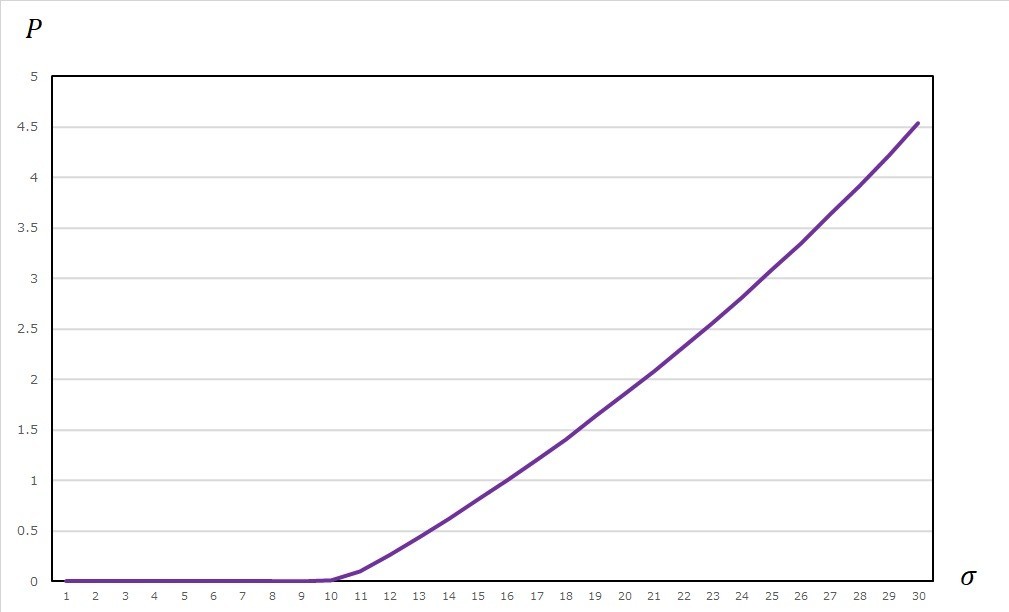
7.9 シミュレーション結果

　上記実装でシミュレーションしてみた結果を以下に掲げる。

7.9.1 ルックバック型最大値オプション

　すべてのパラメータを1つずつ動かして前掲したコードでシミュレーションした。なお動かさないパラメータ値は以下の通りである：

入力パラメータ	概要
初期時点の株価 $S_0$	： $100$
行使価格 $K$	： $80$
無リスク金利 $r$	： $2\%$
ボラティリティ $\sigma$	： $20\%$
満期までの日数 $T$	： $150$ 日
シミュレーション回数 $N$	： $10,000$ 回

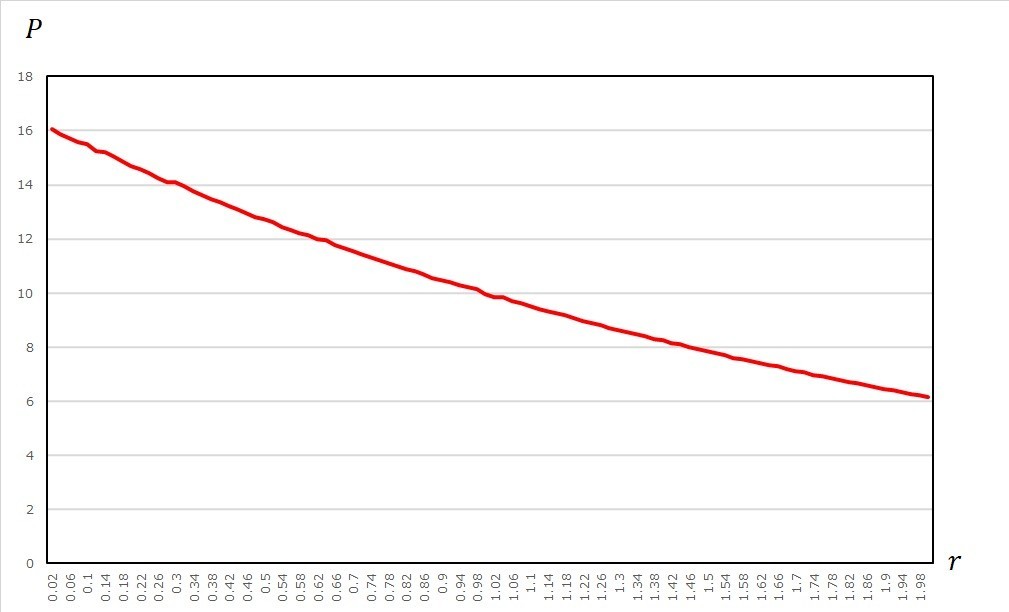
図表1-1　原資産価格 $S$ および行使価格 $K$ を $1$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915033856j:plain

図表1-2　無リスク金利 $r$ を $0.02\%$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915033905j:plain

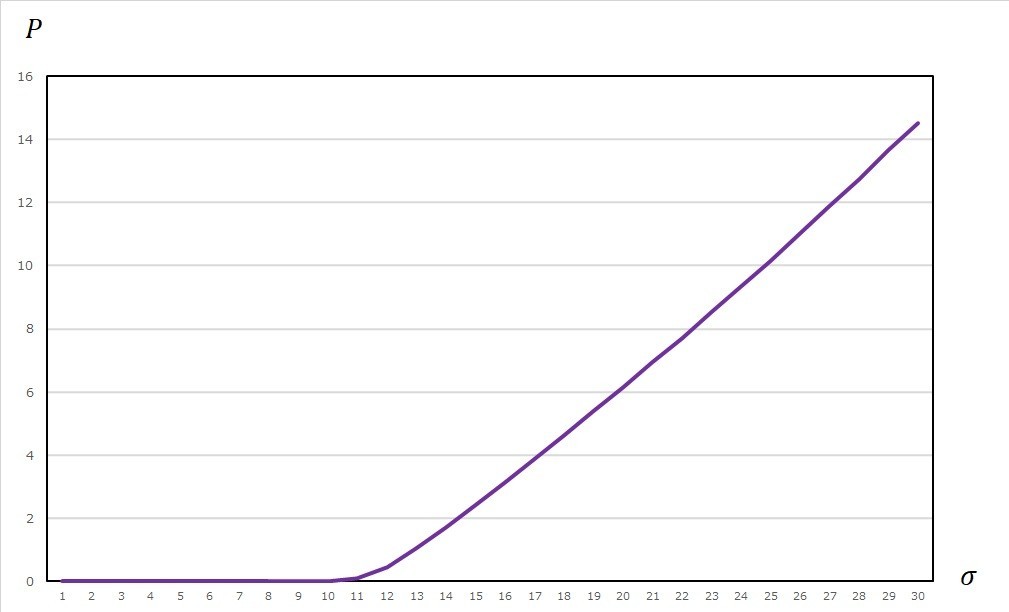
図表1-3　満期 $T$ を $1$ 日ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915033914j:plain

図表1-4　ボラティリティ $\sigma$ を $0.01(=1\%)$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915033923j:plain

図表1-5　シミュレーション回数 $N$ を $50回$ ずつ増やしたときのオプション価格推移
f:id:suguru_125:20210915033932j:plain

7.9.2 ルックバック型平均値オプション

　すべてのパラメータを1つずつ動かして前掲したコードでシミュレーションした。なお動かさないパラメータ値は以下の通りである：

入力パラメータ	概要
初期時点の株価 $S_0$	： $100$
行使価格 $K$	： $80$
無リスク金利 $r$	： $2\%$
ボラティリティ $\sigma$	： $20\%$
満期までの日数 $T$	： $150$ 日
シミュレーション回数 $N$	： $10,000$ 回

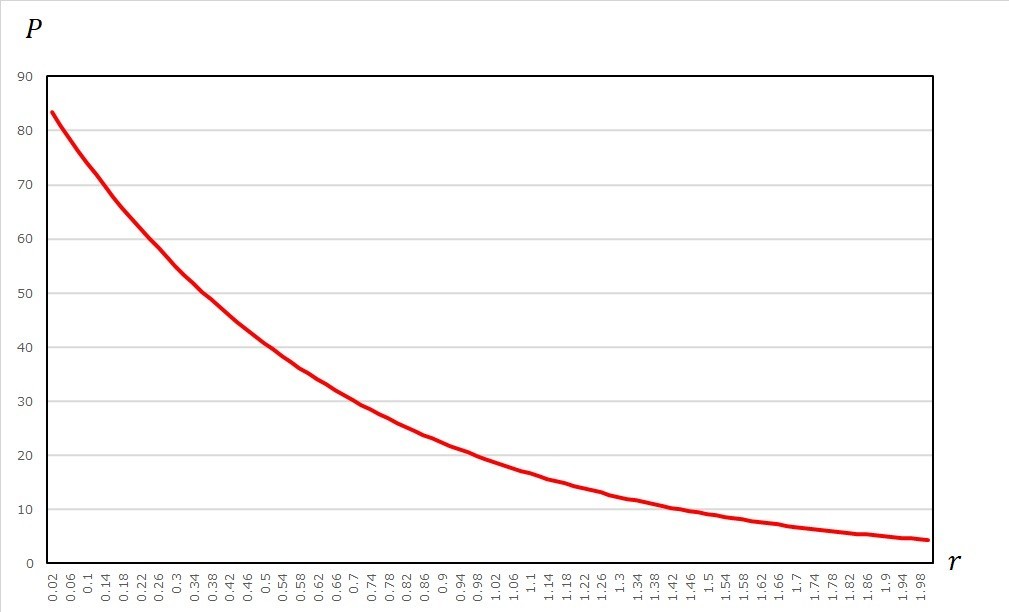
図表2-1　原資産価格 $S$ および行使価格 $K$ を $1$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915033945j:plain

図表2-2　無リスク金利 $r$ を $0.02\%$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915033957j:plain

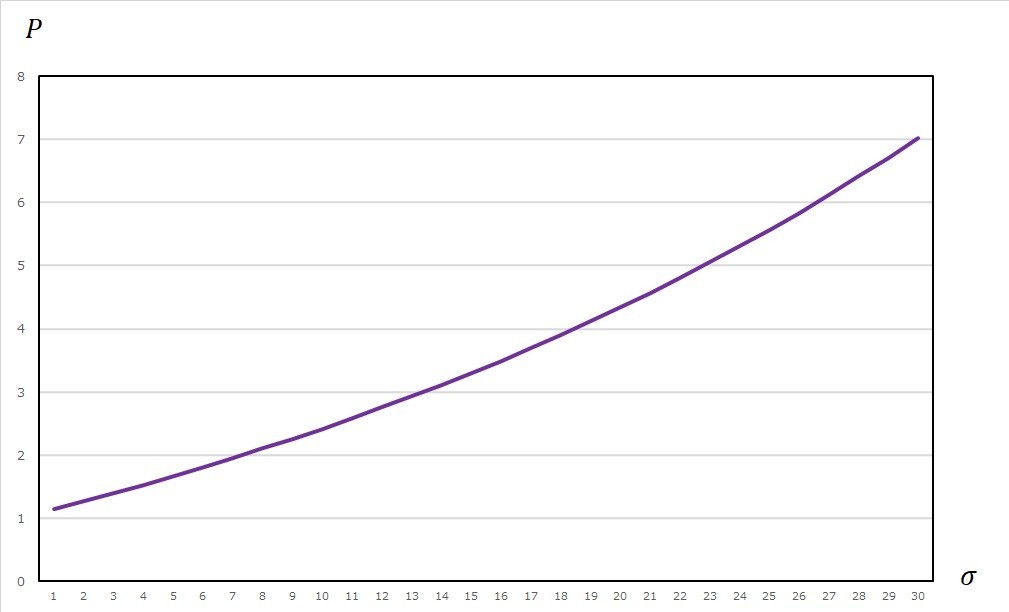
図表2-3　満期 $T$ を $1$ 日ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915034007j:plain

図表2-4　ボラティリティ $\sigma$ を $0.01(=1\%)$ ずつ動かしたときのオプション価格推移
f:id:suguru_125:20210915034016j:plain

図表2-5　シミュレーション回数 $N$ を $50回$ ずつ増やしたときのオプション価格推移
f:id:suguru_125:20210915034025j:plain

7.9.3 ルックバック型デイ・カウント・オプション

　すべてのパラメータを1つずつ動かして前掲したコードでシミュレーションした。なお動かさないパラメータ値は以下の通りである：

入力パラメータ	概要
初期時点の株価 $S_0$	： $100$
基準株価 $\bar{S}$	： $50$
行使価格 $K$	： $80$
無リスク金利 $r$	： $2\%$
ボラティリティ $\sigma$	： $20\%$
基準日数 $\bar{c}$	： $15$ 日
満期までの日数 $T$	： $150$ 日
シミュレーション回数 $N$	： $10,000$ 回