ファイナンス練習(2021年09月04日) - 「大人の教養・知識・気付き」を伸ばすブログ

　業務でC#を用いることになったので、最近勉強していなくて朧気になってきた知識をReviseする意味でも、以下の書籍を読みながらC#で実装してみる。今日はP.79-85まで（当分は実装なしが続きます）。

EXCEL&VBAで学ぶファイナンスの数理

Amazon

4. 多変量確率変数とポートフォリオ理論

4. 多変量確率変数とポートフォリオ理論

4.7 ポートフォリオの最適化

4.7.2 リスクとリターン

　金融商品のリターン $r_{i}$ *1が確率変数であり、その平均および分散が $\mu_{i}, {\sigma_{i}}^2(\sigma_{i}\gt0)$ であるとする。このとき $\omega_{i}$ をウェイトとして

$\begin{aligned} E[\displaystyle{\sum_{i}^{n}\omega_{i}r_{i}}]&=\sum_{i=1}^{n}\omega_{i}\mu_{i}\\ V[\displaystyle{\sum_{i}^{n}\omega_{i}r_{i}}]&=\sum_{i=1}^{n}\sum_{j=1}^{n}\omega_{i}\omega_{j}Cov[r_{i},r_{j}] \end{aligned}$

である。これにより、ポートフォリオ $P$ のリターン $\mu_{P}$ およびリスク $\sigma_{P}$ を

$\begin{aligned} \mu_{P}&=\sum_{i=1}^{n}\omega_{i}\mu_{i}\\ \sigma_{P}&=\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n}\omega_{i}\omega_{j}Cov[r_{i},r_{j}]} \end{aligned}$

と定式化できる。
　リスク回避的な投資家であれば、ある要求値をリターン $\mu_{P}$ として得るようにしつつリスク $\sigma_{P}$ を最小化するようにウェイト $\omega_{1},\cdots,\omega_{n}$ を決めてやれば最適なポートフォリオを構築できることとなる*2。ポートフォリオに条件を付けるのであれば、それを制約条件として加える。たとえば、空売り（信用売り）を許容しないのであれば

$\begin{aligned} ^{\forall}i=1,\cdots,n(\omega_{i}\gt0), \displaystyle{\sum_{i=1}^{n}\omega_{i}=1} \end{aligned}$

を追加する。
　ウェイトを動かしたときのリスクとリターンは、簡単のために $n=2$ とすると以下のような領域を描く。

図1：2証券のリスク・リターンの関係
（ $\mu_{1}=5\%,\sigma_{1}=40\%,\mu_{2}=1\%,\sigma_{2}=10\%$ ）
f:id:suguru_125:20210903213428j:plain

　このような領域で表示されるのは、相関係数を決めていなかったからで、実際には2証券を選べばその相関係数も決まるため、その領域内を通る曲線である。たとえば領域の左端の曲線は $\rho_{12}=1$ のときに得られるものであり、右端のものは $\rho_{12}=-1$ で得られるものである。 $n\geq3$ となれば内部も取り得る。
　このように投資対象となる商品が定まったときに、それらへ投資することで組成できるポートフォリオが取り得る期待リターン $\mu$ とリスク $\sigma$ のペアすべてを集めた集合 $\{(\sigma_{P},\mu_{P})|\}$ を投資機会集合という。

4.8 有効フロンティアと資本市場線

4.8.1 有効フロンティア

　前節での議論で述べたように、複数の商品があるとき、それらへの投資比率が変わることで様々なリスク・リターン*3の組み合わせ（ポートフォリオ）を作ることが出来、それを投資機会集合と呼ぶのであった。とはいえ、投資機会集合は取り得るすべてのリスク・リターンの組み合わせである以上、実際の投資ではその中の1つを選ばなければならない。どうやって選択するのが合理的であろうか。

　投資家がリスク回避的であれば、同じリターンを与えるポートフォリオが複数あるときにはその中でも最もリスクが小さいものを選択する。前節の図で言えば、最も左の境界を与える曲線上の点を与えるような投資比率 $(\omega_{1},\omega_{2})$ を投資家は選ぶことになる。このように、リスク回避的であるときに候補となり得るリスク・リターンの集合を有効フロンティアという（明らかに有効フロンティアは投資機会集合の部分集合である。）。
　以上の条件設定での有効フロンティアを与えるような、空売りを許容せずに要求期待リターン $\mu_{0}\$ を確保しつつリスクを最小化するように投資比率を決定する問題をより詳細に定式化すれば、以下のような最適化問題に帰着することが出来る：

$\begin{aligned} \min_{(\omega_1,\cdots\omega_{n})\in\mathbb{R}^n}{\sigma_{P}}&=\min_{(\omega_1,\cdots\omega_{n})\in\mathbb{R}^n}{\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n}\omega_{i}\omega_{j}Cov[r_{i},r_{j}]}}\\ s.t.\ \ &\sum_{i=1}^{n}\omega_{i}\mu_{i}=\mu_{0},\\ & \omega_{i}\geq0,\cdots, \omega_{n}\geq0,\\ & \displaystyle{\sum_{i=1}^{n}\omega_{i}=1} \end{aligned}$

　さて有効フロンティアを描くことができたとしても、では有効フロンティア上のどの点を選べばよいかという問題が残っている。有効フロンティアは、

投資家はリスク回避的であること
期待リターンはある一定水準を確保すること
（ウェイトへの制約などの）ポートフォリオに与えるべき制約を掛けた上でリスクを最小にするような投資比率を与える

という手続きを経たときに得られるポートフォリオが取り得る $(\sigma,\mu)$ を考えたものであった。したがって、実際に得たい期待リターンの値 $\mu=\mu_{0}$ があるのであれば、有効フロンティアを $\mu=f(\sigma)=f(\omega_{1},\cdots,\omega_{n})$ とおけば、

${\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} \mu=\mu_{0} \\ \mu=f(\omega_{1},\cdots,\omega_{n}) \end{array} \right. \end{eqnarray} }$

の解 $\hat{\omega}_{1},\cdots,\hat{\omega}_{n}$ が知りたかった投資比率である。より簡単に言えば、両者の交点を与えるような投資比率を求めればよい。

4.8.2 資本市場線

　もし無リスク資産（ $\sigma_{F}=0$ かつ $\mu_{F}\neq0$ *4）が存在するならば、更に投資可能な資金のうち、無リスク資産とポートフォリオのどちらにどれだけの資金を振り分けるかという問題になる（ポートフォリオに振り分けた金額を自分が投資対象としたいポートフォリオを与えるような投資比率で投資してやればよい）。
　ポートフォリオ $P$ （期待リターンおよびリスク： $(\mu_P,\sigma_P)$ ）および無リスク資産（期待リターンおよびリスク： $(\mu_{F},\sigma_{F}), \sigma_{F}=0$ ）があるとし、それぞれへの投資比率を $\omega_P,\omega_F=1-\omega_P$ とする（無論、無リスク資産はリスクが $0$ 、すなわち確率変数ではないため、これらの共分散は $0$ である）。ポートフォリオ $P$ および無リスク資産からなるそのような新たなポートフォリオ $P^{\prime}$ の期待リターンおよびリスク $(\mu_{P^{\prime}},\sigma_{P^{\prime}})$ はこれまでの結果から、

$\begin{aligned} \mu_{P^{\prime}}&=\omega_{P}\mu_{P}+\omega_{F}\mu_{F}=\omega_{P}\mu_{P}+(1-\omega_{P})\mu_{F},\\ \sigma_{P^{\prime}}&=\sqrt{(\omega_{P}\sigma_{P})^2+(\omega_{F}\sigma_{F})^2+2\omega_{P}\omega_{F}\cdot0}=\omega_{P}\sigma_{P} \end{aligned}$

となる。これはリスク・リターン平面において、ポートフォリオ $P$ のリスク・リターンを同平面上で意味する点 $P$ および無リスク資産を同平面上で表す点 $X$ とを $\omega_{P}:(1-\omega_{P})$ の比率で内分する点が、無リスク資産とポートフォリオを組み合わせたリスク・リターンを表すことを意味する。

図2：有効フロンティアと接点ポートフォリオの関係
（ $\mu_{1}=5\%,\sigma_{1}=40\%,\mu_{2}=1\%,\sigma_{2}=10\%$ ）
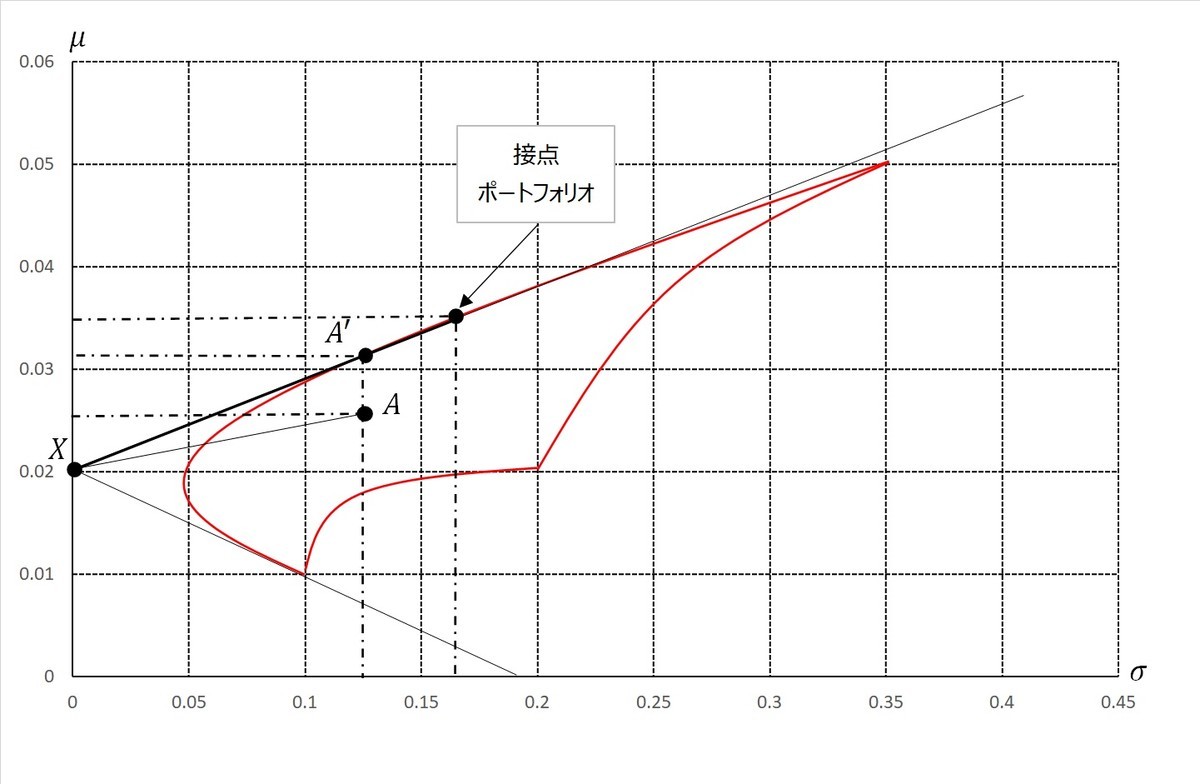
f:id:suguru_125:20210904014736j:plain

　先程のリスク・リターン平面で考えてみよう。無リスク資産は $\mu$ 軸上に存在する（図2の点 $X$ ）。ポートフォリオは投資機会集合（図2で言えば赤線の境界およびその内部）内の任意の点である。直前の議論から、あるポートフォリオ $P$ （を表す点 $A$ ）を決めると、無リスク資産とそのポートフォリオ $P$ からなる新たなポートフォリオ $P^{\prime}$ を表す点は線分 $XA$ 上に存在することになる。ただし、先程の前提

投資家はリスク回避的であること

を考えると、ポートフォリオ $P^{\prime}$ に投資するくらいならば、無リスク資産には投資せず点 $A^{\prime}$ が表すようなポートフォリオに投資した方が、同じリスクでより高い期待リターンをもたらすことが分かる。これはこの平面上において線分 $XA$ の傾きがより大きくなるような点 $A^{\prime}$ が存在することを意味する。とはいえ、ポートフォリオを表す点は投資機会集合を外れることはできない。したがって、無リスク資産がある場合には、無リスク資産を表す点から有効フロンティアに向けて引いた接線との接点が投資すべきポートフォリオの $(\sigma,\mu)$ を与えるのである。この接点のことを接点ポートフォリオという。
　接点ポートフォリオのリスク・リターンを $(\sigma_{tp},\mu_{tp})$ とおけば、この接線自体は、傾きを $a$ として

$\begin{aligned} \mu-\mu_{tp}=a(\sigma-\sigma_{tp}) \end{aligned}$

であり、更にこれは無リスク資産を表す点 $(0,\mu_{F})$ を通るのであるから、 $a=\frac{\mu_{tp}-\mu_{F}}{\sigma_{tp}}$ である。したがってこの接線は

$\begin{aligned} \mu&=\displaystyle{\frac{\mu_{tp}-\mu_{F}}{\sigma_{tp}}(\sigma-\sigma_{tp})+\mu_{tp}}\\ &=\displaystyle{\mu_{F}+(\mu_{tp}-\mu_{F})\frac{\sigma}{\sigma_{tp}}}\\ \end{aligned}$