時系列解析の基礎(29/XX) - 「大人の教養・知識・気付き」を伸ばすブログ

　以下の書籍

基礎からわかる時系列分析―Rで実践するカルマンフィルタ・MCMC・粒子フィルタ― Data Science Library

作者:萩原淳一郎,瓜生真也,牧山幸史
技術評論社

Amazon

を中心に時系列解析を勉強していきます。

前回

power-of-awareness.com

前回
15.　一般状態空間モデルの一括解法

15.　一般状態空間モデルの一括解法

15.1　MCMC

　これまで議論してきた線形・ $\mathrm{Gauss}$ 型状態空間モデルは解を解析的に導出できた。しかし一般的な状態空間モデルでは基本的に解析的な解の導出は不可能である。計算機能力が上がってきた現在では、数値的に解を導出するのが一般的になってきた。その手法の1つに $\mathrm{Markov}$ 連鎖 $\mathrm{Monte}$ $\mathrm{Carlo}$ 法( $\mathrm{MCMC}$ )を用いる方法がある。

15.2　MCMCによる状態の推定

　 $\mathrm{MCMC}$ を活用した平滑化では、推定対象の分布を同時事後分布 $F(\boldsymbol{x}_{0:T}\left|\right.y_{1:T})$ として扱うのが一般的である。更に母数を確率変数として捉える場合、同時事後分布は $F(\boldsymbol{x}_{0:T},\boldsymbol{\theta}\left|\right.y_{1:T})$ となる。
　 $\mathrm{MCMC}$ を活用して同時事後分布から標本を得る方法を考える。ここでは $\mathrm{Gibbs}$ 法によるサンプリングを考える。

1. 初期値 $\boldsymbol{\theta}^{(0)}$ を準備する。
2. $i=1,\cdots,I$ に対して
　a. $F(\boldsymbol{x}_{0:T}|\boldsymbol{\theta}=\boldsymbol{\theta}^{(i-1)},y_{1:T})$ から $\boldsymbol{x}_{0:T}^{(i)}$ をサンプリングする。
　b. $F(\boldsymbol{\theta}|\boldsymbol{x}_{0:T}^{(i)},y_{1:T})$ から $\boldsymbol{\theta}^{(i)}$ をサンプリングする。
3. $\left\{\boldsymbol{x}_{0:T}^{(i)},\boldsymbol{\theta}^{(i)}\right\},i=1,\cdots,I$ を $F(\boldsymbol{x}_{0:T},\boldsymbol{\theta}\left|\right.y_{1:T})$ からの標本とする。

ここで $I$ は $\mathrm{Markov}$ 連鎖の計算における総繰り返し回数であり、ある繰り返し $i$ における変数の実現値を $\cdot^{(i)}$ と表す。

　もし線形・ $\mathrm{Gauss}$ 型状態空間モデルを用いる場合、前向きフィルタ後ろ向きサンプリング( $\mathrm{FFBS}$ )と呼ばれる特別に効率の良いアルゴリズムが存在する。

1. 母数を $\boldsymbol{\theta}^{(i-1)}$ としてカルマン・フィルタリングを行なう。
2. $\mathcal{N}\left(\boldsymbol{m}_T,\boldsymbol{C}_T\right)$ から $\boldsymbol{x}_T$ をサンプリングする。
3. $t=T-1,\cdots,0$ に対して
　a. 平滑化利得 $\boldsymbol{A}_t=\boldsymbol{C}_t{}^{t}\boldsymbol{G}_{t+1}\boldsymbol{R}_{t+1}^{-1}$ とする。
　b. $\mathcal{N}\left(\boldsymbol{h}_t,\boldsymbol{H}_t\right)$ から $\boldsymbol{x}_t$ をサンプリングする。ここで $\boldsymbol{h}_t=\boldsymbol{m}_t+\boldsymbol{A}_t(\boldsymbol{x}_{t+1}-\boldsymbol{a}_{t+1}),$
　　　 $\boldsymbol{H}_t=\boldsymbol{C}_t+\boldsymbol{A}_t\left(\boldsymbol{O}-\boldsymbol{R}_{t+1}\right){}^{t}\boldsymbol{A}_t$ である。

15.3　ライブラリの活用

　 $\mathrm{R}$ で状態空間モデルを活用するパッケージに $\mathrm{dlm}$ や $\mathrm{bsts}$ がある。
　一方で外部ソフトウェアには $\mathrm{WinBUGS}$ や $\mathrm{Stan}$ がある。

15.3.1　例：人工的なローカルレベルモデル

　ここでは $\mathrm{Stan}$ や $\mathrm{MCMC}$ の使い方に習熟すべく、人工データを基にシミュレーションを行なってみる。

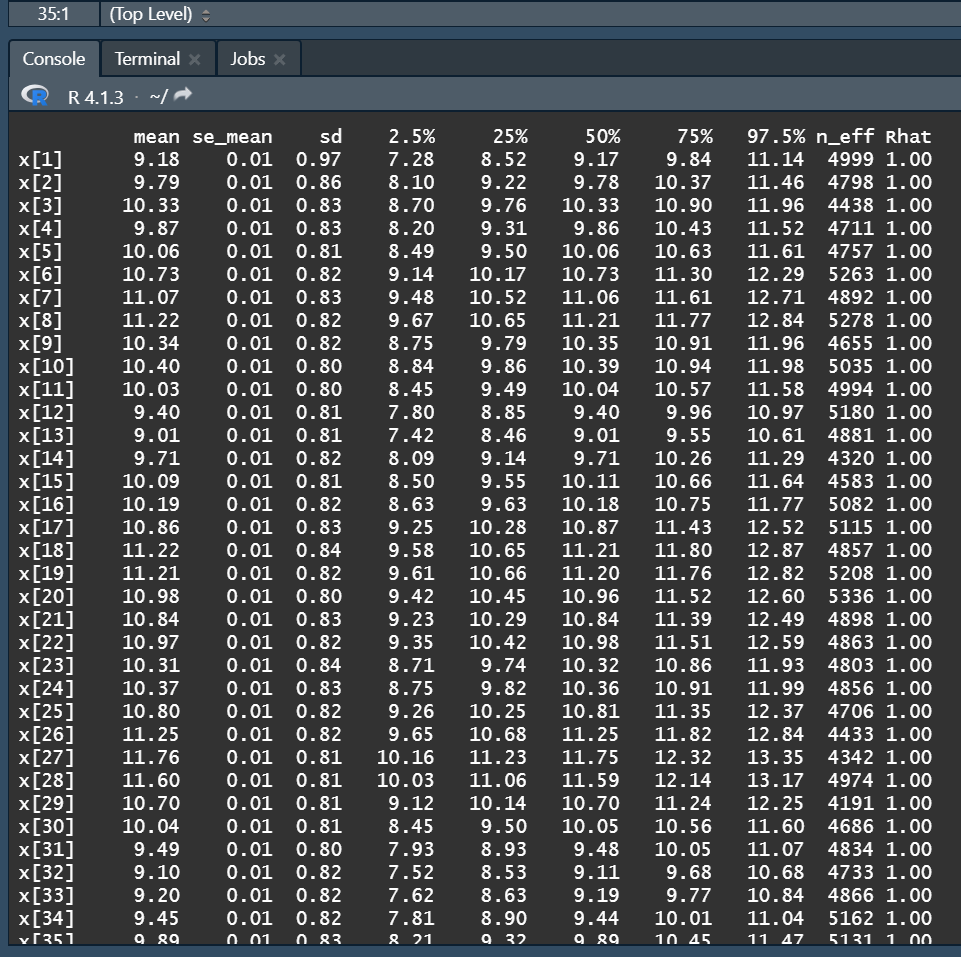
set.seed(123)
library(rstan)

# 人工データの生成
library(dlm)

W <- 1
V <- 2
m0 <- 10
C0 <- 9

mod <- dlmModPoly(order = 1, dW = W, dV = V, m0 = m0, C0 = C0)

t_max <- 200
sim_data <- dlmForecast(mod = mod, nAhead = t_max, sampleNew = 1)
y <- sim_data$newObs[[1]]

# Stanの利用準備
rstan_options(auto_write = T)
options(mc.cores = parallel::detectCores())
theme_set(theme_get() + theme(aspect.ratio = 3/4))

stan_mod_out <- stan_model(file = ".../model10_1.stan")

fit_stan <- sampling(object = stan_mod_out,
                     data = list(t_max = t_max, y = y[,1],
                                 W = mod$W, V = mod$V,
                                 m0 = mod$m0, C0 = mod$C0),
                     pars = c("x"),
                     seed = 123)
oldpar <- par(no.readonly = T)
options(max.print = 99999)
fit_stan

options(oldpar)
traceplot(fit_stan, pars = c(sprintf("x[%d]", 100), "lp__"), alpha = 0.5)

stan_mcmc_out <- rstan::extract(fit_stan, pars = "x")
str(stan_mcmc_out)

s_mcmc <- colMeans(stan_mcmc_out$x)
s_mcmc_quant <- apply(stan_mcmc_out$x, 2, FUN = quantile, probs = c(0.25, 0.75))

15.3.2　収束の判断

　収束しているか否かは、主に3つの観点から調べる。
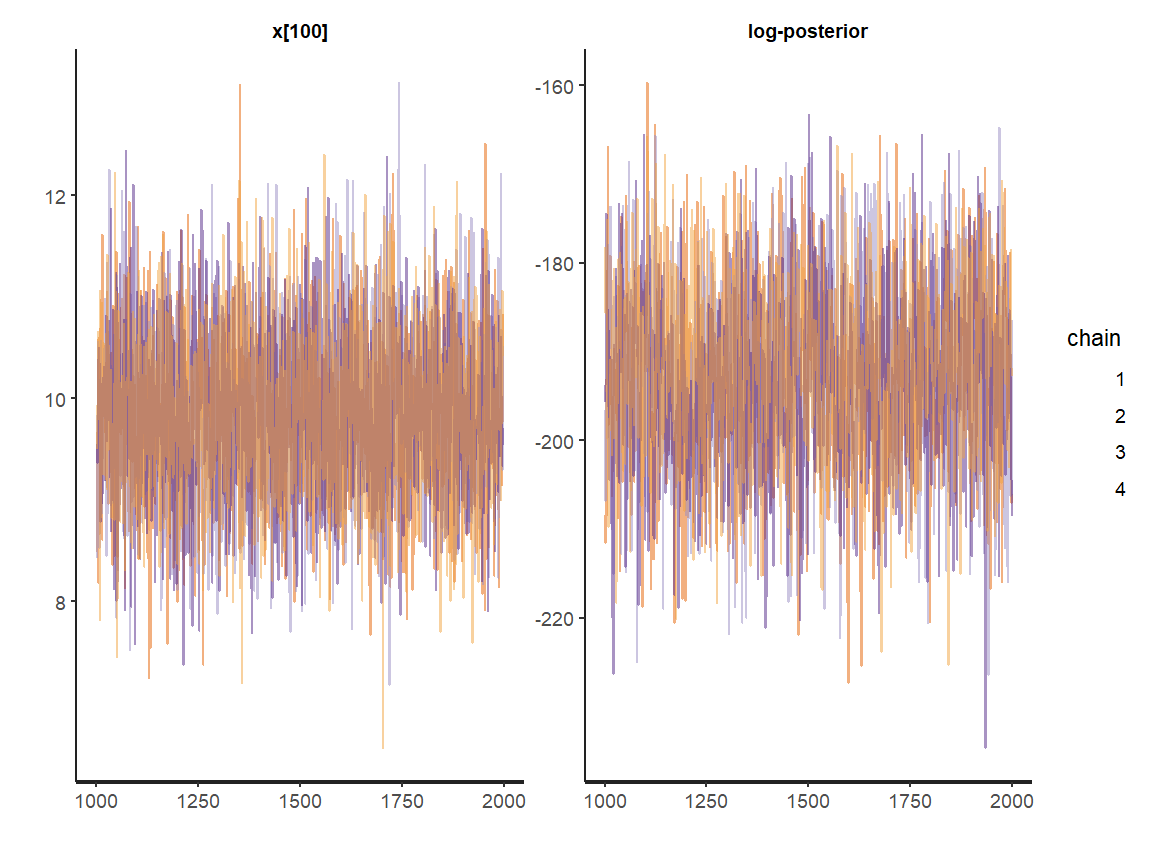
　まずはトレースプロットによる目視である。トレースプロットは、横軸に試行の実行回数（何番目の試行か）、縦軸にその試行において得られた母数の標本の値を取り、それらを折れ線グラフとしてプロットしたグラフである。定常分布が収束しているかを目視で判断する。たとえば各標本値からヒストグラムを作ることでシミュレーションで得たサンプルの標本分布を近似できる。
　次に収束の判断をするための指標として $\mathrm{potential\ scale\ reduction}$

$\begin{aligned} \hat{R}=\sqrt{\displaystyle{\frac{\hat{V}}{\left[\theta|y\right]}}}=\displaystyle{\frac{n-1}{n}}W+\displaystyle{\frac{1}{n}}B \end{aligned}$

がある。ここで $n$ は連鎖の数で、 $W$ は系列間分散*1、 $B$ は系列間分散*2を表す。もし標本が適切な事後分布から生成され、かつ標本サイズが充分に大きければ、 $\hat{R}$ は $1$ に収束する。この指標は標本列の収束性および標本が初期値の依存を脱却したか否かを見ることもできる。すなわち標本が局所最適に陥っていないかを確認できる。 $\mathrm{Gelman}$ $\mathrm{et\ al. (2013)}$ は $\hat{R}\lt1.1$ という判断ルールを提案している*3。
　最後に、分散の観点から標本の収束を確認すべく実効サンプルサイズ( $\mathrm{effective}$ $\mathrm{sample}$ $\mathrm{size}$ )を与える。これは標本間に相関が無いと想定した場合の標本サイズを表している。
　ある母数 $\theta_0$ の推定量 $\theta$ を得たとき、それの相関を持つ系列の平均 $\bar{\theta}$ の分散 $V\left[\bar{\theta}\right]$ に対して

$\begin{aligned} \displaystyle{\lim_{n\rightarrow\infty}mn V\left[\bar{\theta}\right]}=\left(1+2\displaystyle{\sum_{t=1}^{\infty}\rho_t}\right)V\left[\theta|y\right] \end{aligned}$

が成り立つ。ここで $m$ は連鎖の数、 $n$ は繰り返し回数で、 $\rho_t$ は $\theta$ のラグ $t$ の自己相関(系列相関)を表す。もし各 $m$ 連鎖の繰り返しが独立であるならば、 $V\left[\bar{\theta}\right]$ は単純に $\displaystyle{\frac{1}{mn}V\left[\theta|y\right]}$ に一致し、標本サイズは $mn$ に一致する。相関の存在する中では、実効標本サイズは

$\begin{aligned} n_{\mathrm{eff}}=\displaystyle{\frac{mn}{1+\displaystyle{\sum_{t=1}^{\infty}\rho_t}}} \end{aligned}$

で定義される。ただし自己相関は未知であるから、自己相関をその推定値 $\hat{\rho}_t$ に置き換えた

$\begin{aligned} \hat{n}_{\mathrm{eff}}=\displaystyle{\frac{mn}{1+\displaystyle{\sum_{t=1}^{\infty}\hat{\rho}_t}}} \end{aligned}$

を実際には用いる。 $n_{\mathrm{eff}}$ が $mn$ になるべく近いことが望ましいが、 $\mathrm{Gelman}$ $\mathrm{et\ al. (2013)}$ は $\hat{n}_{\mathrm{eff}}\gt 5m$ *4を満たすまではシミュレーションをすべきだというルールを提案している。

　上の例では、トレースプロットを見る限り、目立った異常は生じていない。また $\hat{R}$ はすべて $1.00$ とほぼ収束していると言えそうである。さらに $\hat{n}_{\mathrm{eff}}$ は $5m=5,000$ *5に概ね近い値になっているため、これも満たしたと言い切ることにする。

*1:各繰り返しに関する分散

*2:各連鎖に対する分散

*3:Gelman, Andrew, Carlin, John B., Stern, Hal S., Dunson, David B., Vehtari, Aki, Rubin, Donald B., (2013) "Bayesian Data Analysis, Third Edition, " (CRC Press) P.287

*4:Ibid.

*5:バーンイン期間を踏まえると $m=1,000$ である。

前回

15. 一般状態空間モデルの一括解法

15.1 MCMC

15.2 MCMCによる状態の推定

15.3 ライブラリの活用

15.3.1 例：人工的なローカルレベルモデル

15.3.2 収束の判断