Juliaを使うときのTipsをまとめる（その04/X）

　を使うのに、今一度

Juliaプログラミングクックブック ―言語仕様からデータ分析、機械学習、数値計算まで

で使い方を整理する。

前回

power-of-awareness.com

注意

　参照文献はかなり古い(2019年)ため、現在のバージョンでは動作しない関数などが多いとの評判がある。そこでそういった齟齬があった場合は随時コメントする。なお筆者の環境は、

アプリケーション	バージョン

である。

1.　データ構造とアルゴリズム

　に組み込まれた機能を利用しつつ実用的なカスタムアルゴリズムを実装する方法を紹介する。

1.4　標準的でない基準でデータをソートする

###############################################################
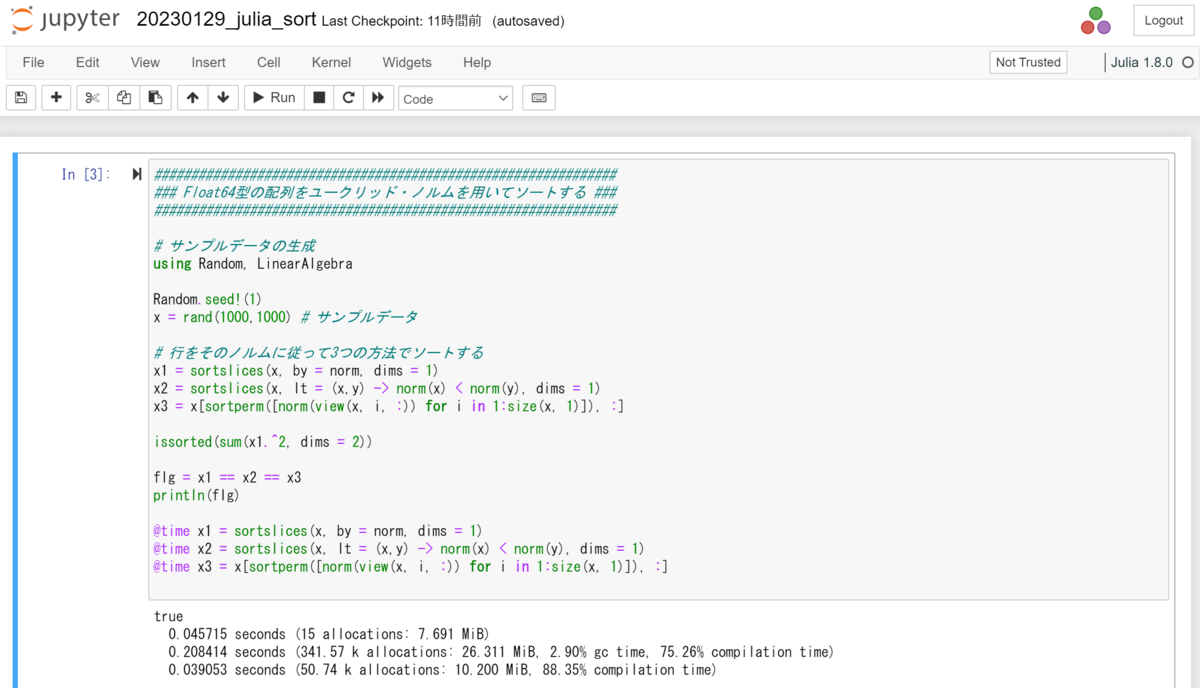
### Float64型の配列をユークリッド・ノルムを用いてソートする ###
###############################################################

# サンプルデータの生成
using Random, LinearAlgebra

Random.seed!(1)
x = rand(1000,1000) # サンプルデータ

# 行をそのノルムに従って3つの方法でソートする
x1 = sortslices(x, by = norm, dims = 1)
x2 = sortslices(x, lt = (x,y) -> norm(x) < norm(y), dims = 1)
x3 = x[sortperm([norm(view(x, i, :)) for i in 1:size(x, 1)]), :]

issorted(sum(x1.^2, dims = 2))

flg = x1 == x2 == x3
println(flg)

@time x1 = sortslices(x, by = norm, dims = 1)
@time x2 = sortslices(x, lt = (x,y) -> norm(x) < norm(y), dims = 1)
@time x3 = x[sortperm([norm(view(x, i, :)) for i in 1:size(x, 1)]), :]

1.4.1　Juliaにおけるソート

　の関数はのような1次元の配列を対象とする。関数を用いることで、行列の行ないし列をソートすることができる。前述のように関数の引数を変えることで、カスタマイズが可能である。

• ：　要素のペアを比較する関数を指定できる。
• ：　比較する前にデータを変換する方法を指定できる。

また関数を用いて並べ替え配列を取得し、これを用いて元のデータからソートされたデータに変換することもできる。
　実行結果からも推察されるように、関数が高速である*1。

1.4.2　実装上の補足

　他にも!や!を用いることも考えておく。

1.5　写像の逆像を生成する

　の型および型を活用して、写像の逆像を生成することとする。
　なお写像において、を満たすようなを逆像(または原像)という*2。

　例として、を考える。

############################
### 写像の逆像を生成する ###
############################

# 逆像を保存するデータ構造の定義
preimage = Dict{Float64, Set{Tuple{Float64, Float64}}}()

# 写像φ(x,y) = x/yを記録
for x in -2.0:2.0, y in -2.0:2.0
    k = x / y
    v = (x, y)
    if haskey(preimage, k)
        push!(preimage[k], v)
    else
        preimage[k] = Set([v])
    end
end

# 整形
for k in sort!(collect(keys(preimage)))
    println(k, ":\t", join(sort!(collect(preimage[k])),"\t"))
end

1.5.1　実装内容

• まずは逆像を保存するデータ構造(辞書型)を定義する。具体的にはキー値を型、値を2つの型からなるタプルとした。
• 次に、定義域をそれぞれ刻みでからまで動かして写像の像を計算する。そしてその像が既にキーとして登録されていれば、定義した辞書に格納済みである集合に!関数でタプルを追加する。他方で像の値が初めて出現した場合、新しい集合を作成する。
• 最後に、データ構造を整形する。キー値とエントリーの双方をソートすべく、とをそれぞれ配列に変換し、!関数でソートさせた。

1.5.2　補足

#####################################
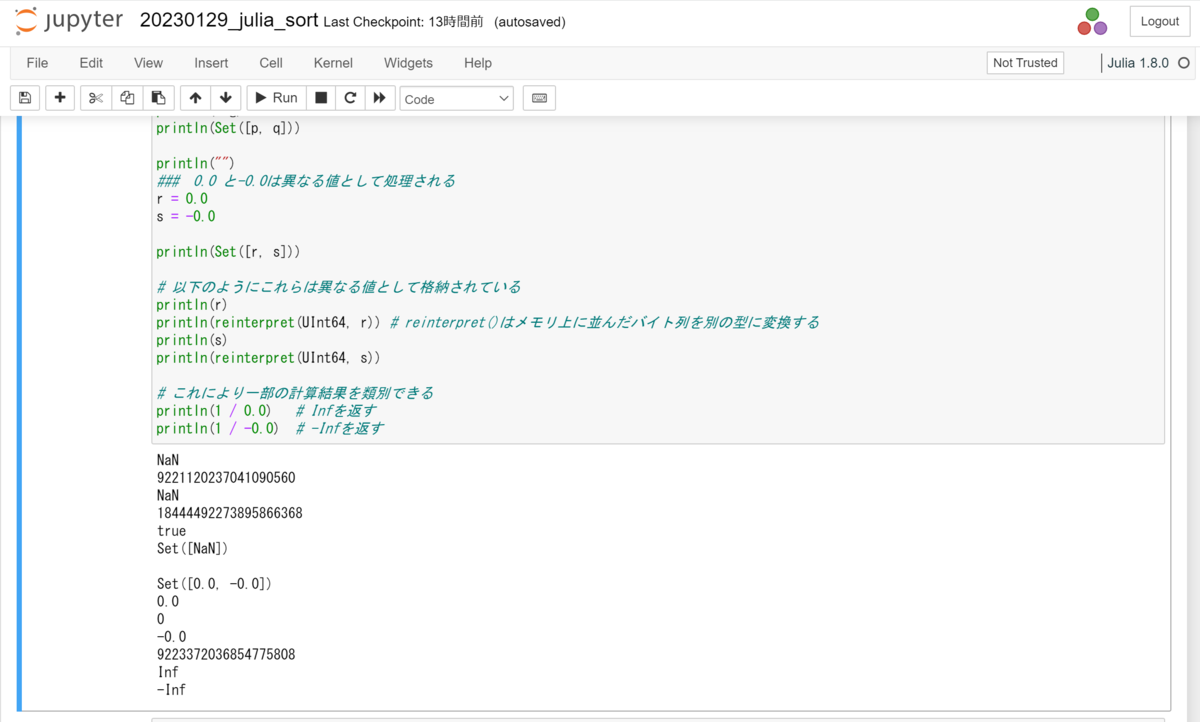
### Juliaにおける特殊値の取り扱い ###
#####################################

### NaNは-1を掛けてもNaNとして扱われる
p = NaN
q = -NaN

# 以下のようにこれらは異なる値として格納されている
println(p)
println(reinterpret(UInt64, p)) # reinterpret()はメモリ上に並んだバイト列を別の型に変換する
println(q)
println(reinterpret(UInt64, q))

# しかし同じ値として処理されている
flg = isequal(p, q) # NaNの等値チェックをisequal()で用いる
println(flg)
println(Set([p, q]))

println("")
###  0.0 と-0.0は異なる値として処理される
r = 0.0
s = -0.0

println(Set([r, s]))

# 以下のようにこれらは異なる値として格納されている
println(r)
println(reinterpret(UInt64, r)) # reinterpret()はメモリ上に並んだバイト列を別の型に変換する
println(s)
println(reinterpret(UInt64, s))

# これにより一部の計算結果を類別できる
println(1 / 0.0)   # Infを返す
println(1 / -0.0)  # -Infを返す

次回

power-of-awareness.com

*1:参考文献ではそれぞれの結果が0.120219s, 0.314779sおよび0.071230sとなっており、明確に1番目の結果が速かった。バージョンアップの間に1番目の内部実装が変更されたのかもしれない。

*2:参考文献では関数の逆像という言い方と写像の逆像という言い方が混同している。関数は写像の特殊例であるから、実装例はそうではないものの、この実装における主旨としては写像の逆像という言い方が精確であると判断する（辞書型は原像が異なるもののその像が一致するものを異なる要素として格納できるため。）。