時系列解析の基礎(30/XX) - 「大人の教養・知識・気付き」を伸ばすブログ

　以下の書籍

基礎からわかる時系列分析―Rで実践するカルマンフィルタ・MCMC・粒子フィルタ― Data Science Library

作者:萩原淳一郎,瓜生真也,牧山幸史
技術評論社

Amazon

を中心に時系列解析を勉強していきます。

前回

power-of-awareness.com

前回
15.　一般状態空間モデルの一括解法
- 15.4　推定精度向上のためのテクニック
  - 15.4.1　線形・型状態空間モデルが部分的に当てはまる場合
次回

15.　一般状態空間モデルの一括解法

15.4　推定精度向上のためのテクニック

　 $\mathrm{MCMC}$ は繰り返し数を無限にした際に理想的な性能を達成することができる。これに対して現実の実装では繰り返し数は有限であるから、その理想的な性能よりも劣化する。そのためより少ない繰り返し数で性能を維持すべく、アルゴリズムから実装に及ぶまで様々な改善手法が提案されている。

15.4.1　線形・ $\mathrm{Gauss}$ 型状態空間モデルが部分的に当てはまる場合

　一部の一般状態空間モデルでは、部分的に線形・ $\mathrm{Gauss}$ 型状態空間モデルが部分的に当てはまることがある。この場合、カルマンフィルタを解法の部品として用いる方法がある。
　このような方法が活用できるのは、一般状態空間モデルにおける状態が線形 $\mathrm{Gauss}$ 型状態空間モデルに従う部分とそれ以外に分離できる場合である。たとえば母数が未知の線形 $\mathrm{Gauss}$ 型状態空間モデルにおいて、母数を確率変数と捉え、状態と母数の同時事後分布 $P\left(\boldsymbol{x}_{0:T},\boldsymbol{\theta}\left|\right.y_{1:T}\right)$ を推定する場合である。母数が既知であったり、母数が道でも状態とは別に予め最尤推定などで求めた値を用いたりすれば、線形 $\mathrm{Gauss}$ 型状態空間モデルだったところが、状態と母数を併せて推定すべく一般状態空間モデルとしたのだった。そのため母数が分かれば線形 $\mathrm{Gauss}$ 型状態空間モデルに帰着し得る。
　そのための方法の1つが、確率変数として考えている母数だけを $\mathrm{MCMC}$ で推定し、その推定結果を $\mathrm{Karman\ filter}$ で利用するものである。この場合、

$\begin{aligned} P\left(\boldsymbol{\theta}\left|\right.y_{1:T}\right) \end{aligned}$

が $\mathrm{MCMC}$ の推定対象である。このとき $\mathrm{Bayes}$ の定理から

$\begin{aligned} P\left(\boldsymbol{\theta}\left|\right.y_{1:T}\right)\propto P\left(y_{1:T}\left|\right.\boldsymbol{\theta}\right)P\left(\boldsymbol{\theta}\right) \end{aligned}$

が成り立つ。 $P\left(y_{1:T}\left|\right.\boldsymbol{\theta}\right)$ は線形 $\mathrm{Gauss}$ 型状態空間モデルの尤度であるから、

$\begin{aligned} l(\boldsymbol{\theta})&=\displaystyle{\sum_{t=1}^{T}\log p\left(y_t\left|\right.y_{1:t-1};\boldsymbol{\theta}\right)}\\ &=-\displaystyle{\frac{1}{2}\sum_{t=1}^{T}\log\left|Q_t\right|}-\displaystyle{\frac{1}{2}\sum_{t=1}^{T}\frac{(y_t-f_t)}{Q_t}} \end{aligned}$

とすればよい( $f_t$ および $Q_t$ は一期先予測尤度の平均および分散である。)。 $p\left(\boldsymbol{\theta}\right)$ には無情報事前分布を設定することが多い。こうして得た $\boldsymbol{\theta}$ の推定結果の代表値を点推定値として $\mathrm{Karman}$ $\mathrm{filter}$ に用いる。
　2つ目の方法は、同時事後分布 $p\left(\boldsymbol{x}_{0:T},\boldsymbol{\theta}\left|\right.y_{1:T}\right)$ からの標本を得る方法で、前向きフィルタ後ろ向きサンプリング( $\mathrm{FFBS}$ )が利用できる。1項目の $p\left(\boldsymbol{x}_{0:T}\left|\right.\boldsymbol{\theta},y_{1:T}\right)$ は $\boldsymbol{\theta}$ が既知という条件となっており、線形 $\mathrm{Gauss}$ 型状態空間モデルに従う。ここからのサンプリングには $\mathrm{FFBS}$ を用いる。2項目の $p\left(\boldsymbol{\theta}\left|\right.y_{1:T}\right)$ のサンプリングには1つ目の方法を適用する。まずは2項目からのサンプリングを行ない、その後 $\mathrm{FFBS}$ を用いて1項目のからサンプリングを行ない、状態の標本を生成する。
　いずれの方法でも、 $\mathrm{MCMC}$ による推定対象は母数に限定される。

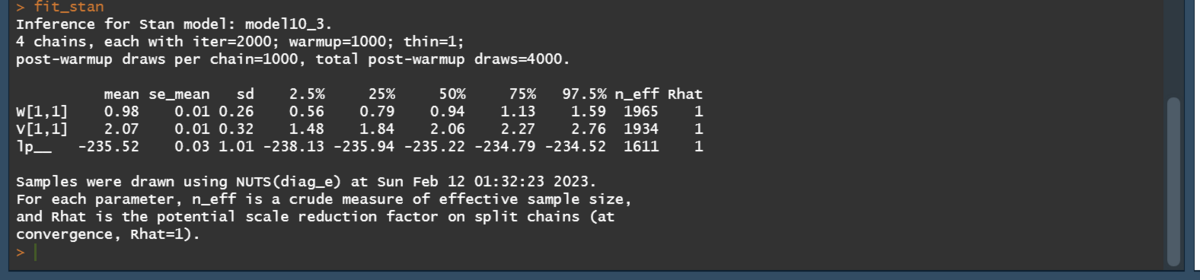
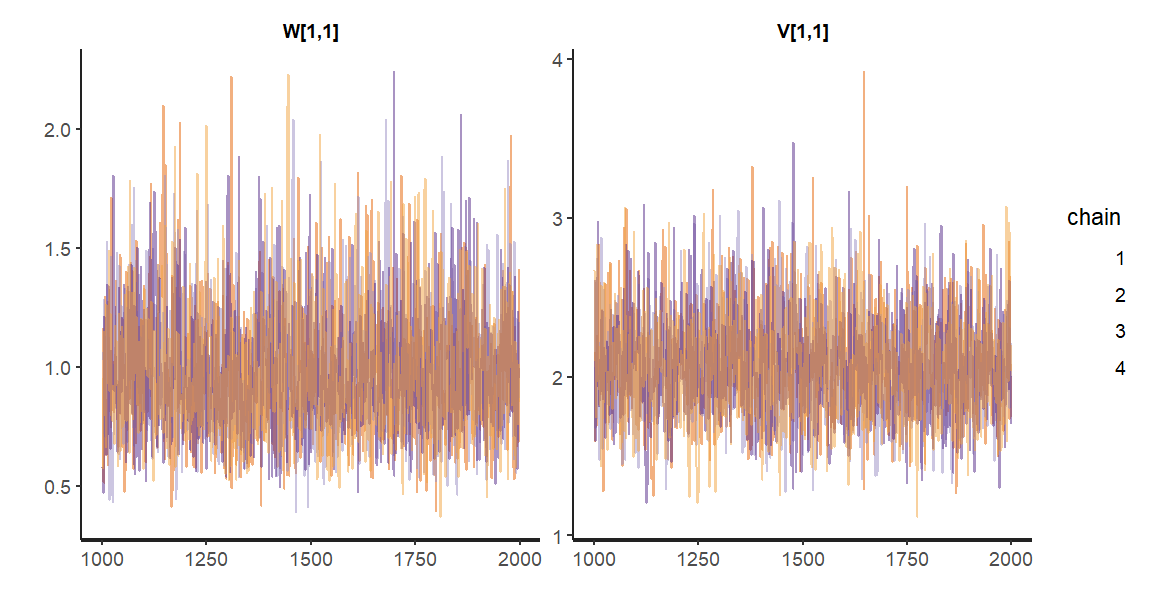
set.seed(123)
library("rstan")
library("dlm")

# stanの事前設定
rstan_options(auto_write = T)
options(mc.cores = parallel::detectCores())
theme_set(theme_get() + theme(aspect.ratio = 3/4))

# 
load(file = "C:/Users/Julie/Desktop/ArtifitialLocalLevelModel.RData")

# モデル：生成・コンパイル
stan_mod_out <- stan_model(file = "C:/Users/Julie/Desktop/model10_3.stan")

# 平滑化：実行（サンプリング）
dim(mod$m0) <- 1
fit_stan <- sampling(object = stan_mod_out,
                     data = list(t_max = t_max, y = matrix(y, nrow = 1),
                                 G = mod$G, F = t(mod$F),
                                 m0 = mod$m0, C0 = mod$C0),
                     pars = c("W","V"),
                     seed = 123
                     )
# 結果
fit_stan

traceplot(fit_stan, pars = c("W", "V"), alpha = 0.5)

# 必要なサンプリング結果を取り出す
stan_mcmc_out <- rstan::extract(fit_stan, pars = c("W", "V"))

# FFBSの前処理
it_seq <- seq_along(stan_mcmc_out$V[,1,1])
progress_bar <- txtProgressBar(min = 1, max = max(it_seq), style = 3)

# FFBSの本処理
x_FFBS <- sapply(it_seq, function(it){
  # 進捗バー
  setTxtProgressBar(pb = progress_bar, value = it)
  
  mod$W[1,1] <- stan_mcmc_out$W[it,1,1]
  mod$V[1,1] <- stan_mcmc_out$V[it,1,1]
  
  return(dlmBSample(dlmFilter(y = y, mod = mod)))
})

# FFBSの後処理
x_FFBS <- t(x_FFBS[-1,])

# 周辺化
s_FFBS <- colMeans(x_FFBS)
s_FFBS_quant <- apply(x_FFBS, 2, FUN = quantile, probs = c(0.25, 0.5, 0.75))

s_FFBS_quant