以下の書籍
を中心に時系列解析を勉強していきます。
13. 線形・Gauss型状態空間モデルの逐次解法
13.1. カルマンフィルタ
線形・型状態空間モデルにおいて、推定すべきデータの真の値と点推定値の間の平均二乗誤差を最小にする意味で最適な逐次推定法はカルマンフィルタと呼ばれる。カルマンフィルタは非定常過程でも扱うことができる。カルマンフィルタで行なわれる計算はすべて線形計算で、正規分布の再生性から関心の対象となる分布はすべて正規分布である。
カルマンフィルタにおいて前提とする線形・型状態空間モデルは
で、は
次状態遷移行列、
は
[観測行列、
は
次状態雑音の共分散行列、そして
は観測雑音の分散である。また
で、
は事前分布における
次元平均ベクトルで、
は
次分散共分散行列である。したがってこのモデルにおける推定パラメータ
は
である。
13.1.1 カルマンフィルタリング
カルマンフィルタリングにおけるフィルタリング分布、一期先予測分布および一期先予測尤度を
| フィルタリング分布 |
平均ベクトル |
|
|---|---|---|
| 一期先予測分布 |
平均ベクトル |
|
| 一期先予測尤度 |
平均 |
と書くものとする。
時点でのフィルタリング分布からその翌時点
時点におけるフィルタリング分布は、以下のアルゴリズムで推定する。
| 0. | 時点 |
|
| 1. | 時点 |
|
| 一期先予測分布 (平均) |
||
| 2. | 時点 |
これをから繰り返すことで全時点のフィルタリング分布を求める。
なおカルマン利得は、一期先予測分布を補正してフィルタリング分布を求める際の補正の程度を表す量である。具体的には、観測値と一期先予測尤度の平均
との差を予測誤差
と置くときに、補正において予測誤差をどの程度反映するかのウェイトという意味合いを持つ。カルマン利得の値には
と
の比が支配的な影響を及ぼす。
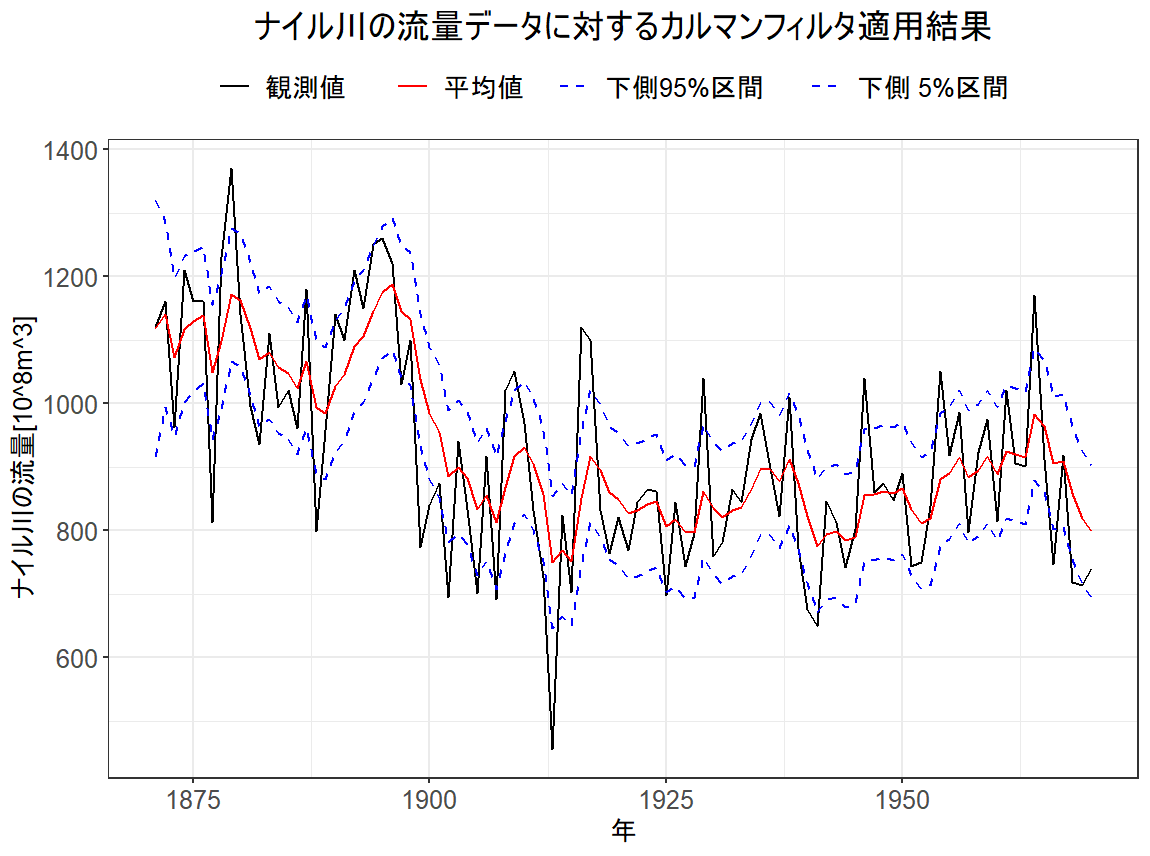
############################ ### 自作カルマンフィルタ ### ############################ library("ggplot2") # データ y <- Nile t_max <- length(y) # 1時点分のカルマンフィルタリングを行なう関数 Kalman_filtering <- function(m_t_minus_1, C_t_minus_1, t){ # 一期先予測分布 a_t <- G_t %*% m_t_minus_1 R_t <- G_t %*% C_t_minus_1 %*% t(G_t) + W_t # 一期先予測尤度 f_t <- F_t %*% a_t Q_t <- F_t %*% R_t %*% t(F_t) + V_t # カルマン利得 K_t <- R_t %*% t(F_t) %*% solve(Q_t) # 状態の更新 m_t <- a_t + K_t %*% (y[t]-f_t) C_t <- (diag(nrow(R_t)) - K_t %*% F_t) %*% R_t # フィルタリング分布 list(m = m_t, C = C_t, a = a_t, R = R_t) } # 線形ガウス型状態空間のパラメータを設定 G_t <- matrix(1, ncol = 1, nrow = 1) W_t <- matrix(exp(7.29), ncol = 1, nrow = 1) F_t <- matrix(1, ncol = 1, nrow = 1) V_t <- matrix(exp(9.62), ncol = 1, nrow = 1) m0 <- matrix(0, ncol = 1, nrow = 1) C0 <- matrix(1e+7, ncol = 1, nrow = 1) # フィルタリング分布 # 状態の領域を確保 m <- rep(NA_real_, t_max) C <- rep(NA_real_, t_max) a <- rep(NA_real_, t_max) R <- rep(NA_real_, t_max) # 時点t=1 KF <- Kalman_filtering(m_t_minus_1 = m0,C_t_minus_1 = C0,t = 1) m[1] <- KF$m C[1] <- KF$C a[1] <- KF$a R[1] <- KF$R #時点t=2-t_max for (t in 2:t_max){ KF <- Kalman_filtering(m_t_minus_1 = m[t-1],C_t_minus_1 = C[t-1],t = t) m[t] <- KF$m C[t] <- KF$C a[t] <- KF$a R[t] <- KF$R } # フィルタリングの結果 filtering_data <- data.frame(time = as.numeric(time(y)), var = "観測値", val = as.numeric(y)) filtering_data <- rbind(filtering_data,data.frame(time = as.numeric(time(y)), var = "平均値", val = m)) filtering_data <- rbind(filtering_data,data.frame(time = as.numeric(time(y)), var = "下側95%区間", val = mapply(FUN = function(m,v)qnorm(p = 0.95,mean = m,sd = sqrt(v)),m,C))) filtering_data <- rbind(filtering_data,data.frame(time = as.numeric(time(y)), var = "下側 5%区間", val = mapply(FUN = function(m,v)qnorm(p = 0.05,mean = m,sd = sqrt(v)),m,C))) filtering_data$var <- factor(filtering_data$var,levels = c("観測値","平均値","下側95%区間","下側 5%区間")) # グラフ g <- ggplot(data = filtering_data,mapping = aes(x = time, y = val,group = var, color = var, linetype = var)) g <- g + geom_line(size = 0.6) + theme_bw() g <- g + labs(title = "ナイル川の流量データに対するカルマンフィルタ適用結果", x = "年",y = paste0("ナイル川の流量[",expression(10^8),expression(m^3),"]"),group = "",color = "", linetype = "") g <- g + theme(axis.text= element_text(size = 12), axis.text.x=element_text(size = 12), legend.title = element_blank(), legend.text = element_text(size = 12), legend.position = "top", axis.title = element_text(size = 12), axis.title.y = element_text(angle = 90,size = 12), plot.title= element_text(size = 16,hjust = 0.5)) g <- g + scale_linetype_manual(values = c("solid","solid","dashed","dashed")) g <- g + scale_color_manual(values = c("black","red","blue","blue")) plot(g)