以下の書籍
を中心に時系列解析を勉強していきます。
13. 線形・Gauss型状態空間モデルの逐次解法
13.1. カルマンフィルタ
線形・型状態空間モデルにおいて、推定すべきデータの真の値と点推定値の間の平均二乗誤差を最小にする意味で最適な逐次推定法はカルマンフィルタと呼ばれる。カルマンフィルタは非定常過程でも扱うことができる。カルマンフィルタで行なわれる計算はすべて線形計算で、正規分布の再生性から関心の対象となる分布はすべて正規分布である。
13.1.2 カルマン予測
線形形状態空間モデルでは
期先予測分布も正規分布になることから、
期先予測モデルを
とおく。このとき時点期先予測分布から時点
期先予測分布は以下で求めることができる:
| 0. | 時点 |
|
| 1. | 時点 |
|
| 2. | 時点 |
もし欠損値があった場合、フィルタリングのアルゴリズムにおいてカルマン利得をとおいて一期先予測分布をフィルタリング分布と見なすことでフィルタリングの手続きを進めていく。
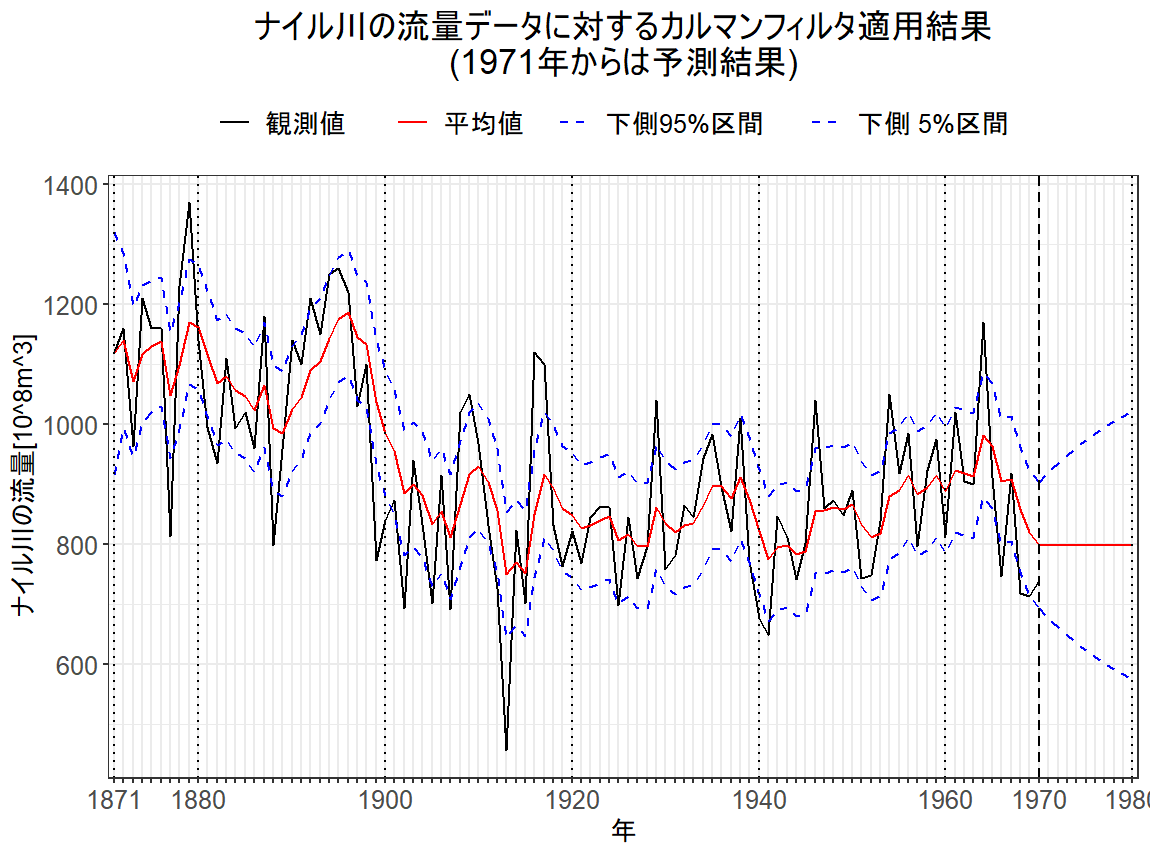
################################ ### 自作カルマンフィルタ予測 ### ################################ library("ggplot2") ### カルマンフィルタリングが完了していることが前提 if(T){ # データ y <- Nile t_max <- length(y) # 1時点分のカルマンフィルタリングを行なう関数 Kalman_filtering <- function(m_t_minus_1, C_t_minus_1, t){ # 一期先予測分布 a_t <- G_t %*% m_t_minus_1 R_t <- G_t %*% C_t_minus_1 %*% t(G_t) + W_t # 一期先予測尤度 f_t <- F_t %*% a_t Q_t <- F_t %*% R_t %*% t(F_t) + V_t # カルマン利得 K_t <- R_t %*% t(F_t) %*% solve(Q_t) # 状態の更新 m_t <- a_t + K_t %*% (y[t]-f_t) C_t <- (diag(nrow(R_t)) - K_t %*% F_t) %*% R_t # フィルタリング分布 list(m = m_t, C = C_t, a = a_t, R = R_t) } # 線形ガウス型状態空間のパラメータを設定 G_t <- matrix(1, ncol = 1, nrow = 1) W_t <- matrix(exp(7.29), ncol = 1, nrow = 1) F_t <- matrix(1, ncol = 1, nrow = 1) V_t <- matrix(exp(9.62), ncol = 1, nrow = 1) m0 <- matrix(0, ncol = 1, nrow = 1) C0 <- matrix(1e+7, ncol = 1, nrow = 1) # フィルタリング分布 # 状態の領域を確保 m <- rep(NA_real_, t_max) C <- rep(NA_real_, t_max) a <- rep(NA_real_, t_max) R <- rep(NA_real_, t_max) # 時点t=1 KF <- Kalman_filtering(m_t_minus_1 = m0,C_t_minus_1 = C0,t = 1) m[1] <- KF$m C[1] <- KF$C a[1] <- KF$a R[1] <- KF$R #時点t=2-t_max for (t in 2:t_max){ KF <- Kalman_filtering(m_t_minus_1 = m[t-1],C_t_minus_1 = C[t-1],t = t) m[t] <- KF$m C[t] <- KF$C a[t] <- KF$a R[t] <- KF$R } # フィルタリングの結果 filtering_data <- data.frame(time = as.numeric(time(y)), var = "観測値", val = as.numeric(y)) filtering_data <- rbind(filtering_data,data.frame(time = as.numeric(time(y)), var = "平均値", val = m)) filtering_data <- rbind(filtering_data,data.frame(time = as.numeric(time(y)), var = "下側95%区間", val = mapply(FUN = function(m,v)qnorm(p = 0.95,mean = m,sd = sqrt(v)),m,C))) filtering_data <- rbind(filtering_data,data.frame(time = as.numeric(time(y)), var = "下側 5%区間", val = mapply(FUN = function(m,v)qnorm(p = 0.05,mean = m,sd = sqrt(v)),m,C))) filtering_data$var <- factor(filtering_data$var,levels = c("観測値","平均値","下側95%区間","下側 5%区間")) } # 予測期間 t <- t_max nAhead <- 10 # 10期先まで予測する kalman_prediction <- function(a_t0, R_t0){ # 1期先予測 a_t1 <- G_t_plus_1 %*% a_t0 R_t1 <- G_t_plus_1 %*% R_t0 %*% t(G_t_plus_1) + W_t_plus_1 list(a = a_t1, R = R_t1) } G_t_plus_1 <- G_t W_t_plus_1 <- W_t ### 線形Gaus型状態空間のパラメータを設定 a_ <- rep(NA_real_, t_max + nAhead) R_ <- rep(NA_real_, t_max + nAhead) # k = 0:フィルタリング分布のパラメータを設定 a_[t+0] <- m[t] R_[t+0] <- C[t] # k = 1~nAhead for(k in 1:nAhead){ KP <- kalman_prediction(a_t0 = a_[t+k-1], R_t0 = R_[t+k-1]) a_[t+k] <- KP$a R_[t+k] <- KP$R } prediction_data <- data.frame(time = c(as.numeric(time(y)),(as.numeric(time(y))[length(time(y))]+(1:nAhead))), var = "平均値", val = a_) prediction_data <- rbind(prediction_data,data.frame(time = c(as.numeric(time(y)),(as.numeric(time(y))[length(time(y))]+(1:nAhead))), var = "下側95%区間", val = mapply(FUN = function(m,v)qnorm(p = 0.95,mean = m,sd = sqrt(v)),a_,R_))) prediction_data <- rbind(prediction_data,data.frame(time = c(as.numeric(time(y)),(as.numeric(time(y))[length(time(y))]+(1:nAhead))), var = "下側 5%区間", val = mapply(FUN = function(m,v)qnorm(p = 0.05,mean = m,sd = sqrt(v)),a_,R_))) prediction_data$var <- factor(filtering_data$var,levels = c("観測値","平均値","下側95%区間","下側 5%区間")) time_labels <- prediction_data$time flg_time_labels <- time_labels%%20==0 flg_time_labels[1] <- T flg_time_labels[length(flg_time_labels)] <- T flg_time_labels[unique(time_labels)==1970] <- T time_labels[!flg_time_labels] <- "" filtering_data$time <- factor(filtering_data$time,levels = unique(prediction_data$time)) prediction_data$time <- factor(prediction_data$time,levels = unique(prediction_data$time)) # g <- ggplot(data = filtering_data,mapping = aes(x = time, y = val,group = var, color = var, linetype = var)) g <- g + geom_line(size = 0.6) + theme_bw() g <- g + geom_line(mapping = aes(x = time, y = val,group = var, color = var, linetype = var),data = prediction_data,size = 0.6) + theme_bw() g <- g + labs(title = "ナイル川の流量データに対するカルマンフィルタ適用結果\n(1971年からは予測結果)", x = "年",y = paste0("ナイル川の流量[",expression(10^8),expression(m^3),"]"),group = "",color = "", linetype = "") g <- g + theme(axis.text= element_text(size = 12), axis.text.x=element_text(size = 12), legend.title = element_blank(), legend.text = element_text(size = 12), legend.position = "top", axis.title = element_text(size = 12), axis.title.y = element_text(angle = 90,size = 12), plot.title= element_text(size = 16,hjust = 0.5)) g <- g + scale_x_discrete(labels = time_labels) g <- g + geom_vline(xintercept = (1:length(flg_time_labels))[flg_time_labels], linetype =3) g <- g + geom_vline(xintercept = (1:length(flg_time_labels))[unique(prediction_data$time)==1970], linetype = 2) g <- g + scale_linetype_manual(values = c("solid","solid","dashed","dashed")) g <- g + scale_color_manual(values = c("black","red","blue","blue")) plot(g)