を参照していく。
前回
6. グラフ構造
ヒトのつながりを表現する手段であるグラフ理論に基づくグラフ構造が利用し得る。
6.4 幅優先探索
6.4.3 深さ優先探索とスタック
深さ優先探索は調べるべき頂点をキューではなくスタックというデータ構造に保存する。スタックは処理するべきデータを積み重ねて保持する。後から来たデータは先に入ったデータの上に積み上がり、最後にスタックへ追加された一番新しいデータが次の処理対象になる。スタックの動作は最後に入ったデータが最初に出ていくことになるため、と呼ばれる。
########################## ### 深さ優先探索の実装 ### ########################## import random def generate_graph(n, m): """ n個の頂点とm個の辺を持つグラフを作る""" graph_data = [[0] * n for i in range(n)] edge_set = set() while len(edge_set) < m: i, j = random.sample(range(n), 2) if i > j: i, j = j, i edge_set.add((i,j)) graph_data[i][j] = graph_data[j][i] = 1 return graph_data, edge_set my_graph, edge_set = generate_graph(16, 20) def depth_first_search(start, W): # リストをスタックとして利用する work_stack = [] visited = set() work_stack.append(start) visited.add(start) while work_stack: here = work_stack.pop() for i, node in enumerate(W[here]): if node == 0: continue if i not in visited: work_stack.append(i) visited.add(i) return visited # 10番目の頂点を始点にする depth_first_search(10, my_graph)
6.5 最短距離を求める
最短距離を求めるアルゴリズムを2つ紹介する。
6.5.1 グラフの最短距離
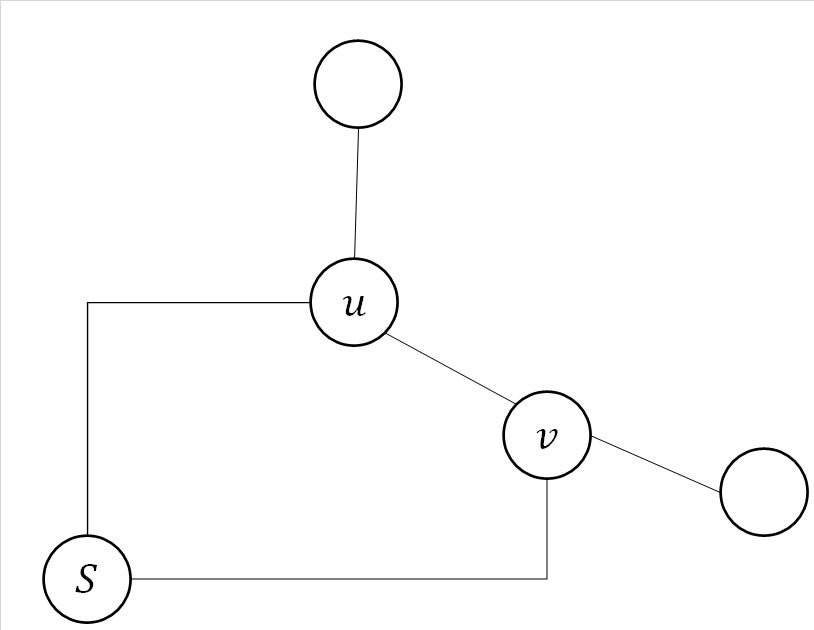
頂点から最短経路の探索を始めて、いま
に到着したという状態を考える。このとき
から
までの最短距離を
とし、これが既知だとする。
と隣接する
への最短距離を考えたい。
もしならば
とする操作を考える。これを緩和という。緩和は
までの最短距離が分かっているという条件の下で
から
までの最短距離を確定する作業である。
 |
これを基にしたアルゴリズムでは、まずすべての頂点にスタートの頂点からの仮の最短距離を割り当てる。そしてそれらを緩和によって順次本当の最短距離にしていく。
6.5.2 ダイクストラ法
辺の重みが負でない場合、ダイクストラ法という方法で最短距離を求めることができる。
ダイクストラ法はある頂点から到達できる他のすべての頂点への最短距離を計算する。
| (1) | ||
| (2) |
このためにヒープ構造を扱う。ヒープは最小値が常に最小値が先頭に来るため、仮の最短距離を更新するたびにその値をヒープに入れればよい。
###################### ### ダイクストラ法 ### ###################### import math import heapq def dijkstra(start, W): """スタートの頂点と隣接行列を受け取り、 到達可能なすべての頂点への最短距離を返す""" # 仮の最短距離∞を設定 distance_list = [math.inf] * len(W) # スタートの頂点だけ距離を0とする distance_list[start] = 0 # 最短距離が確定した頂点 done_list = [] # 次に処理する頂点を決めるためのヒープ wait_heap = [] for i,d in enumerate(distance_list): # (スタートからの距離, 頂点) heapq.heappush(wait_heap, (d, i)) # ヒープが空になるまで続ける while wait_heap: p = heapq.heappop(wait_heap) i = p[1] if i in done_list: continue # この時点でスタートからiへの最短距離が確定する done_list.append(i) # iに隣接するすべての頂点に対する処理 for j, x in enumerate(W[i]): if x==1 and j not in done_list: # 緩和を実行 d = min(distance_list[j], distance_list[i] + x) distance_list[j] = d # jへの仮の最短距離をdとしてヒープに追加 return distance_list dijkstra(10, my_graph)
