Rについて
をベースに学んでいく。
今回は線形回帰分析(PP.133-146)を扱う。
11. 線形回帰分析
データ間の関係の規則を関数式で表し、入力に相当する変数*1を説明変数、出力に相当する変数
を目的変数として
という形式の統計モデルおよびそれをデータから求める分析方法を回帰分析という。説明変数が1つならば単回帰分析、複数ならば重回帰分析という。
11.1 単回帰分析
単回帰モデル
では最小二乗法により
と推定するのが代表的である。
11.2 Rパッケージ
では線形回帰分析のために
がある。
# lm lm(formula, data, weights, subset, na.action,...)
| モデル形式を指定。Ex. y~x(y=ax+b), y~x-1(y=ax) | ||
| 回帰分析に用いるデータセット(データフレーム) | ||
| 説明変数にウェイトを付ける場合のウェイトベクトル | ||
| データセットの中の一部分を用いる場合に指定 | ||
| 欠損値の扱い |
出力は変数に格納するとリスト形式で得られ、以下のような構成になっている*2
| 回帰係数 | |||
| 推定に用いたデータの予測値 | |||
| 残差平方和 | |||
| 回帰係数の分散分析 | |||
| 新たなデータに対する予測値 | |||
| 結果の要約 | |||
| 回帰診断プロット |
11.3 Rでの実行例
11.3.1 単回帰の実行例
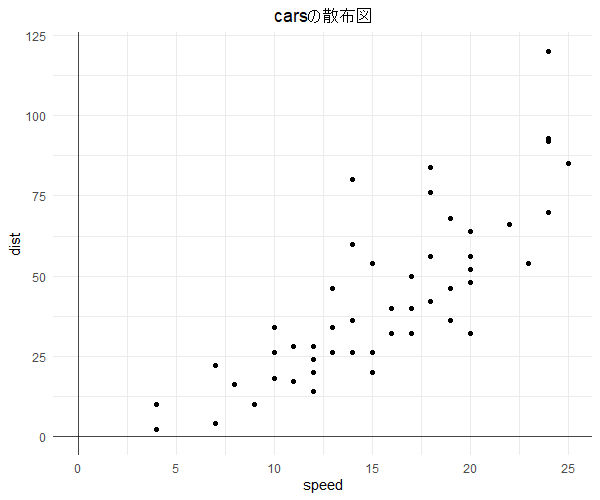
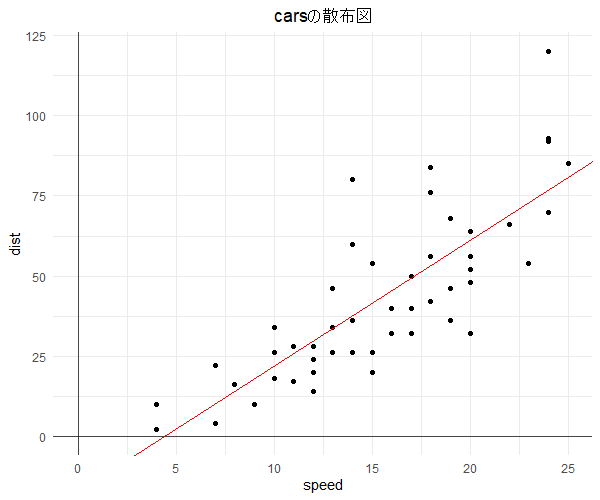
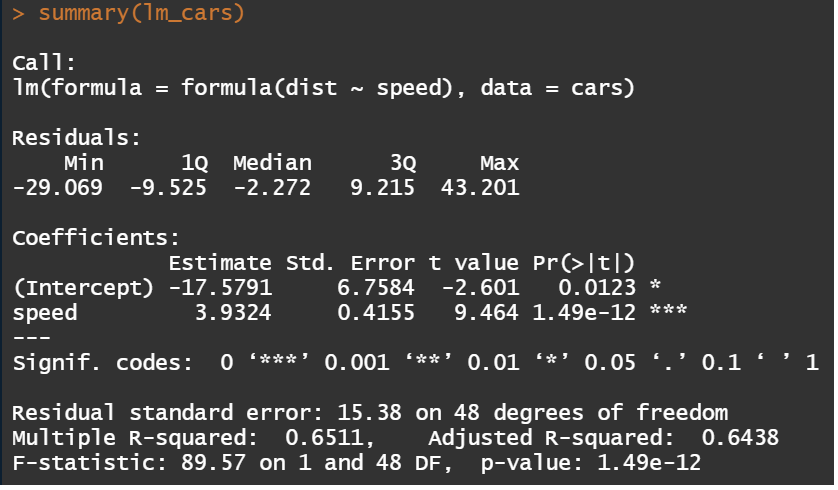
library("ggplot2") ########################################## ### dataとしてcarsを用いて単回帰を実施 ### ########################################## data(cars) # 分布 g <- ggplot(data = cars,mapping = aes(x = speed, y = dist)) + geom_point()+ theme_minimal() + ggtitle("carsの散布図") + theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom", legend.title=element_text(size = 7), legend.text=element_text(size = 7)) g <- g + geom_vline(xintercept = 0,linetype = 1,size = 0.5, alpha = 0.7) g <- g + geom_hline(yintercept = 0,linetype = 1,size = 0.5, alpha = 0.7) plot(g) # 相関の有無を相関係数でも確認 print(cor(x = cars$speed,y = cars$dist,method = "pearson")) # Pearsonの積率相関 print(cor(x = cars$speed,y = cars$dist,method = "kendall")) # Kendallの順位相関 #################### ### 単回帰を実施 ### #################### lm_cars <- lm(formula = formula(dist ~ speed),data = cars) # 結果の要約 summary(lm_cars) # Call: 適用したlm() # Residuals: 残差の特性値 # Coefficients: 回帰結果 # Intercept:回帰切片, speed: 回帰係数 # Estimate: 推定値, Std.Error: 標準誤差, # t value:t値, Pr(>|t|): p値 # Residual standard error: 残差の標準誤差, xx degrees of freedom:自由度 # Multiple R-squared: 決定係数 # Adjusted R-squared: 修正済決定係数 # F-statistic: F値(すべての回帰係数が0であるという帰無仮説の検定統計量) # より簡素な要約 print(lm_cars) # 残差 residuals(lm_cars) # 回帰係数 coefficients(lm_cars) # 推定したモデル:(dist) = -17.579 + 3.932 * (speed) predict(object = lm_cars,newdata = data.frame("speed" = 0:25)) # 回帰直線を追加 g2 <- g + geom_abline(slope = coefficients(lm_cars)[2],intercept = coefficients(lm_cars)[1],colour = "red") plot(g2) # 回帰診断図 op <- par(mfrow = c(2,2)) plot(lm_cars) par(op)
 |
 |
11.3.2 重回帰の実行例
library("ggplot2") library("GGally") ##################### ### 線形重回帰分析 ### ###################### # データセットairqualityを利用 data("airquality") # 散布図行列 ggpairs(airquality[,c(-5,-6)],aes_string(alpha = 0.5)) #################### ### 重回帰を実施 ### #################### lm_airquality <- lm(formula = formula("Ozone ~ Solar.R + Wind + Temp"),data = airquality) # 要約 summary(lm_airquality) # より簡素な要約 print(lm_airquality) # 残差 residuals(lm_airquality) # 回帰係数 coefficients(lm_airquality) # 推定したモデル:(dist) = -17.579 + 3.932 * (speed) # 回帰診断図 op <- par(mfrow = c(2,2)) plot(lm_airquality) par(op)



11.3.3 交互作用モデル
交互作用を考慮した
モデルを考えてみる。
とはいえ、フルモデルが良いものになるとは限らない(実際の推定結果を見てもp値が少し高い)。そこででモデル選択をしてみる。
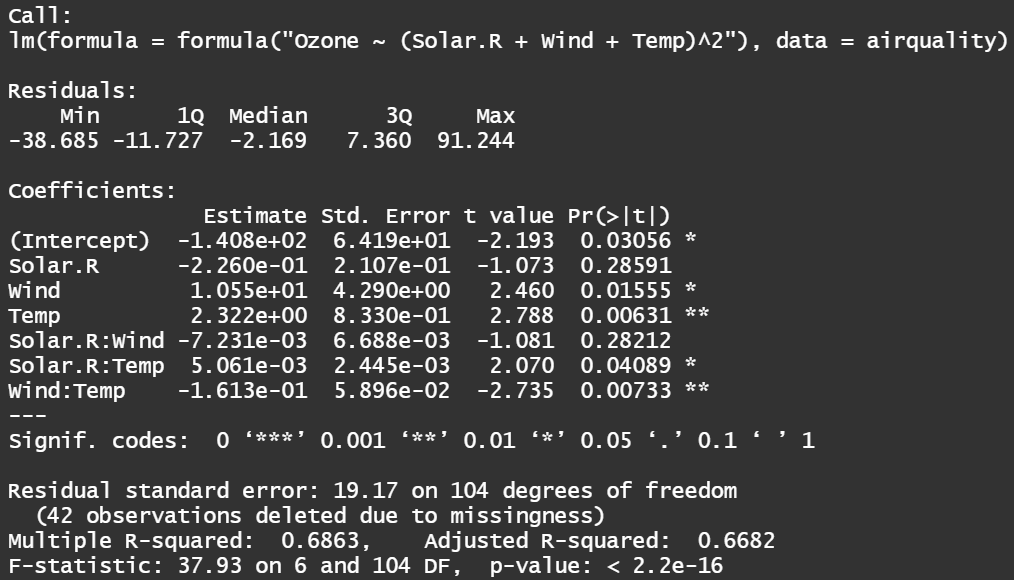
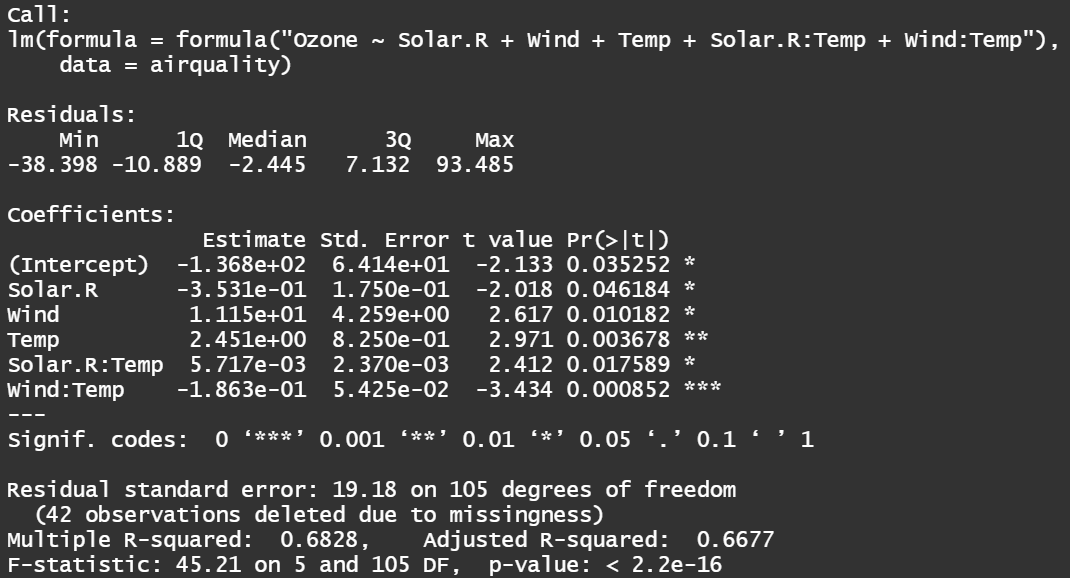
################################ ### 交互作用を追加したモデル ### ################################ lm_airquality2 <- lm(formula = formula("Ozone ~ (Solar.R + Wind + Temp)^2"),data = airquality) summary(lm_airquality2) # AICを用いて変数選択を行うことにする lm_airquality2_AIC <- step(lm_airquality2) # 最もAICの小さい、Solar.R:Windを除いたモデルを選択する # 最終的なモデル lm_airquality_f <- lm(formula = formula("Ozone ~ Solar.R + Wind + Temp + Solar.R:Temp + Wind:Temp"), data = airquality) summary(lm_airquality_f)
モデル選択結果(左:フルモデル,右:選択モデル)
 |
 |