Rによるデータサイエンス（11/21） - 「大人の教養・知識・気付き」を伸ばすブログ

　Rについて

Rによるデータサイエンス(第2版):データ解析の基礎から最新手法まで

作者:金明哲
森北出版

Amazon

をベースに学んでいく。
　今回は非線形回帰分析（PP.147-160）を扱う。

前回
12.　非線形回帰分析
補足　スペック情報

前回

power-of-awareness.com

12.　非線形回帰分析

　目的変数を説明変数の非線形な関数を用いたモデルを用いる場合を扱う。これを非線形モデルと呼ぶ。基本的な手法は線形回帰と同様である。

12.1　ロジスティック回帰

　普及率や成長率、さらには確率などの非線形曲線を当てはめるのに、ロジスティック曲線

$\begin{aligned} y=\displaystyle{\frac{a}{1+be^{cx}}},\ a,b,c,\in\mathbb{R} \end{aligned}$

を用いる場合がある。ロジスティック曲線を用いる回帰分析をロジスティック回帰という。
　 $x,y$ の関係式をロジスティック曲線を用いて直接的に回帰したい場合、 $\mathrm{R}$ では $\mathrm{nls}$ 関数を用いる。

nls(formula, data, start, trace)

他方で、 $y$ を事象の発生有無を表すダミー変数( $y=0$ ならば発生しなかった、 $y=1$ ならば発生した。)、 $p$ を $y=1$ となる確率とし $\boldsymbol{x}$ *1として、発生確率 $p$ を推定したい、もしくは発生の有無を予測したい場合は、パッケージ $\mathrm{VGAM}$ の $\mathrm{vglm}$ 関数を用いる。 $\mathrm{vglm}$ では $x,y$ の直接的な関数形、推定ウェイト、データセットおよび当てはめる統計モデルなどを指定することができる。

12.2　多項式回帰

　 $x,y$ を

$\begin{aligned} y = \beta_0+\beta_1x+\beta_2x^2+\beta_3x^3+\cdots+\beta_{n}x^n+\varepsilon \end{aligned}$

と仮定して推定するのを多項式回帰という。

12.3　一般化線形モデル

　ロジスティック回帰のように、指数型分布族にデータを対応させ非線形の現象を簡単に扱えるようにした回帰である。目的変数は量的変数のみならず、2値データなどでも適用できる。
　説明変数(ベクトル) $\boldsymbol{X},\$ 目的変数(ベクトル) $\boldsymbol{Y},\$ 係数(行列) $A$ および誤差(行列・ベクトル) $\displaystyle{\varepsilon}$ を用いて線形モデルは

$\begin{aligned} \boldsymbol{Y}=\boldsymbol{X}A+\boldsymbol{\varepsilon} \end{aligned}$

で現れる。一般化線形モデルでは、非線形関数を $g(\mu)=\boldsymbol{X}A, \mu=E[\boldsymbol{Y}]$ になるように変換し、線形モデルとして扱う。

12.4　平滑化回帰と加法モデル

　特殊な非線形データではこれまで議論してきた回帰モデルでは当てはまりが悪い。そこで平滑化回帰を行なってみる。ここではアルゴリズムの異なる4つの平滑化回帰を当てはめてみる(次節参照)。
　また加法モデル

$\begin{aligned} y=a+f_1(x_1)+f_2(x_2)+\cdots++f_i(x_i)+\cdots++f_n(x_n)+\varepsilon \end{aligned}$

も考えることができる。
　一般化線形モデルを加法モデル化したものを一般化加法モデルと呼び、 $\mathrm{GAM}$ と略称される。

12.5　シミュレーション

12.5.1　ロジスティック回帰

######################
### 非線形回帰分析 ###
######################

library("ggplot2")

# カラーテレビの普及率
vc_year <- 1966:1984
vc_usage_rate <- c(0.003, 0.016, 0.054, 0.139, 0.263, 0.423, 0.611, 0.758,
                   0.859, 0.903, 0.937, 0.954, 0.978, 0.978, 0.982, 0.985,
                   0.989, 0.988, 0.992)

vc_year_g <- vc_year
flg <- vc_year_g%%5==0
flg[c(1,length(flg))] <- T
vc_year_g[!flg] <- ""

df_usage_rate <- data.frame(year = factor(vc_year,level = vc_year),
                            usage = vc_usage_rate)

g1 <- ggplot(df_usage_rate,aes(x = year, y = usage)) + geom_point()
g1 <- g1 + ggtitle("日本におけるカラーテレビの普及率")
g1 <- g1 + xlab("年") + ylab("普及率")
g1 <- g1 + theme_classic()
g1 <- g1 + scale_x_discrete(breaks = vc_year_g,labels = vc_year_g)
g1 <- g1 + theme(plot.title = element_text(hjust = 0.5),legend.position = "none",
                 text=element_text(size = 12),
                 legend.title=element_text(size = 16),
                 legend.text=element_text(size = 12))
g1 <- g1 + geom_hline(yintercept = seq(0,1,0.25), linetype =3)
plot(g1)

### ロジスティック回帰
df_usage_rate <- data.frame(year = vc_year,
                            usage = vc_usage_rate)


# nls(formula = formula(usage ~ a/(1+b * exp(c*year))), data = df_usage_rate,start = c(a = 1,b = 1,c = -1),trace = T)

df_usage_rate <- data.frame(year = vc_year-vc_year[1],
                            usage = vc_usage_rate)

# yearが大きすぎて推定に失敗するため、初年度(1966年)からの経過年数で推定してみる
ls_est <- nls(formula = formula(usage ~ a/(1+b * exp(c*year))), data = df_usage_rate,start = c(a = 1,b = 1,c = -1),trace = T)

summary(ls_est)$parameters # 母数の推定値

df_usage_rate_obs <- data.frame(year = factor(vc_year,level = vc_year),
                                var = "観測値",
                                usage = vc_usage_rate)
df_usage_rate_est <- data.frame(year = factor(vc_year,level = vc_year),
                                var = "推計値",
                                est = fitted(ls_est))

g2 <- ggplot()
g2 <- g2 + geom_point(data = df_usage_rate_obs,mapping = aes(x = year, y = usage, group = var))
g2 <- g2 + geom_line(data = df_usage_rate_est,mapping = aes(x = year, y = est, group = var, color = "red"))
g2 <- g2 + labs(title = "日本におけるカラーテレビの普及率", subtitle = "(黒点:観測値, 赤線:予測値)",
                x = "年", y = "普及率")
g2 <- g2 + theme_classic()
g2 <- g2 + scale_x_discrete(breaks = vc_year_g,labels = vc_year_g)
g2 <- g2 + theme(plot.title = element_text(hjust = 0.5),
                 plot.subtitle = element_text(hjust = 0.5),
                 legend.position = "none",
                 text=element_text(size = 12),
                 legend.title=element_text(size = 16),
                 legend.text=element_text(size = 12))
g2 <- g2 + geom_hline(yintercept = seq(0,1,0.25), linetype =3)
plot(g2)

12.5.2　多項式回帰

##################
### 多項式回帰 ###
##################

### 人工データの生成
set.seed(1)
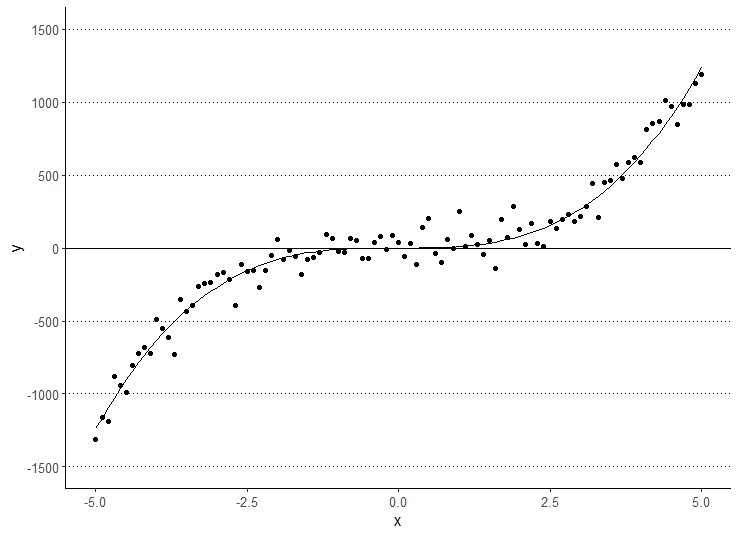
x <- seq(-5,5,0.1)
y <- 10 * x^3 + 100*rnorm(x,0 ,1)

# テストデータ
ggplot(data.frame(x=x,y=y), aes(x=x,y=y)) + geom_point() + 
  theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                 plot.subtitle = element_text(hjust = 0.5),
                 legend.position = "none",
                 text=element_text(size = 12),
                 legend.title=element_text(size = 12),
                 legend.text=element_text(size = 12)) +
  scale_y_continuous(breaks = seq(-1500,1500,500), labels = seq(-1500,1500,500))+ 
  geom_hline(yintercept = seq(-1500,1500,500), linetype = 3) + 
  geom_hline(yintercept = 0, linetype = 1)

# パラメータの推定
fm3 <- nls(y~a + b*x + c*x^2 + d*x^3, start = c(a=1,b=1,c=1,d=1),trace = T)
summary(fm3) # 有意でない係数が多い

# パラメータの推定
fm3_2 <- nls(y~d*x^3, start = c(d=1),trace = T)
summary(fm3_2)

AIC(fm3)
AIC(fm3_2)


ggplot(data.frame(x=x,y=y), aes(x=x,y=y)) + geom_point() + 
  geom_line(data = data.frame(x = x, y= summary(fm3_2)$parameters[1] * x^3),mapping = aes(x=x,y=y))+ 
  theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                          plot.subtitle = element_text(hjust = 0.5),
                          legend.position = "none",
                          text=element_text(size = 12),
                          legend.title=element_text(size = 12),
                          legend.text=element_text(size = 12)) +
  scale_y_continuous(breaks = seq(-1500,1500,500), labels = seq(-1500,1500,500))+ 
  geom_hline(yintercept = seq(-1500,1500,500), linetype = 3) + 
  geom_hline(yintercept = 0, linetype = 1)

12.5.3　一般化線形モデル

########################
### 一般化線形モデル ###
########################

data(airquality)


### モデルの当てはめ
## 重回帰モデル
ls_fit_mg <- lm(formula = formula(Ozone ~ Solar.R+Wind+Temp),data = airquality)

qqnorm(resid(ls_fit_mg))
qqline(resid(ls_fit_mg),lwd = 2, col = "red")

## 残差分布としてガンマ分布を仮定
ls_fit_gamma <- glm(formula = formula(Ozone ~ Solar.R+Wind+Temp),data = airquality, family = Gamma)

AIC(ls_fit_mg)
AIC(ls_fit_gamma) # ガンマ分布を当てはめた方がAICが低いようだ

plot(ls_fit_gamma,which = 2)

12.5.4　平滑化回帰

##################
### 平滑化回帰 ###
##################

### 人工データの生成
set.seed(20)

x1 <- seq(-10,10,0.1)
y1 <- 50 * sin(x1) + x1^2 + 10 * rnorm(length(x1),0,1)

df_data <- data.frame(x = x1, y = y1)

ggplot(df_data,aes(x=x,y=y)) + geom_point() + 
  theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                          plot.subtitle = element_text(hjust = 0.5),
                          legend.position = "none",
                          text=element_text(size = 12),
                          legend.title=element_text(size = 12),
                          legend.text=element_text(size = 12)) +
  scale_y_continuous(breaks = seq(-150,150,50), labels = seq(-150,150,50))+ 
  geom_hline(yintercept = seq(-150,150,50), linetype = 3) + 
  geom_hline(yintercept = 0, linetype = 1)

## まずは多項式回帰
lm_p2 <- fitted(lm(y1 ~ poly(x1,2)))
lm_p5 <- fitted(lm(y1 ~ poly(x1,5)))
lm_p8 <- fitted(lm(y1 ~ poly(x1,8)))

df_fitted <- data.frame(x = x1,
                        var = "2次",
                        y = unlist(lm_p2))
df_fitted <- rbind(df_fitted,data.frame(x = x1,
                                        var = "5次",
                                        y = unlist(lm_p5)))
df_fitted <- rbind(df_fitted,data.frame(x = x1,
                                        var = "8次",
                                        y = unlist(lm_p8)))

ggplot(df_data,aes(x=x,y=y)) + geom_point() + 
  geom_line(data = df_fitted,mapping = aes(x=x,y=y, color = var)) + 
  theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                          plot.subtitle = element_text(hjust = 0.5),
                          legend.position = "bottom",
                          text=element_text(size = 12),
                          legend.title=element_text(size = 12),
                          legend.text=element_text(size = 12)) +
  scale_y_continuous(breaks = seq(-150,150,50), labels = seq(-150,150,50))+ 
  geom_hline(yintercept = seq(-150,150,50), linetype = 3) + 
  geom_hline(yintercept = 0, linetype = 1) #b当てはまりが悪い…

df_fitted2 <- data.frame(x = x1,
                         var = "平滑化スプライン",
                         y = fitted(smooth.spline(x1,y1)))
df_fitted2 <- rbind(df_fitted2,data.frame(x = x1,
                                         var = "Nadaraya-Watson\nカーネル平滑化",
                                         y = ksmooth(x1,y1)$y))
df_fitted2 <- rbind(df_fitted2,data.frame(x = x1,
                                         var = "Friedman\nスーパースムーザー法",
                                         y = supsmu(x1,y1)$y))
df_fitted2 <- rbind(df_fitted2,data.frame(x = x1,
                                         var = "LOWESS平滑化",
                                         y = lowess(x1,y1,f=0.1)$y))
df_fitted2[,"var"] <- factor(df_fitted2[,"var"],levels = c("平滑化スプライン","Nadaraya-Watson\nカーネル平滑化",
                                                           "Friedman\nスーパースムーザー法","LOWESS平滑化"))

ggplot(df_data,aes(x=x,y=y)) + geom_point() + 
  geom_line(data = df_fitted2,mapping = aes(x=x,y=y, color = var)) + 
  labs(color = "") +
  theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                          plot.subtitle = element_text(hjust = 0.5),
                          legend.position = "bottom",
                          text=element_text(size = 12),
                          legend.title=element_text(size = 12),
                          legend.text=element_text(size = 12)) +
  scale_y_continuous(breaks = seq(-150,150,50), labels = seq(-150,150,50))+ 
  geom_hline(yintercept = seq(-150,150,50), linetype = 3) + 
  geom_hline(yintercept = 0, linetype = 1)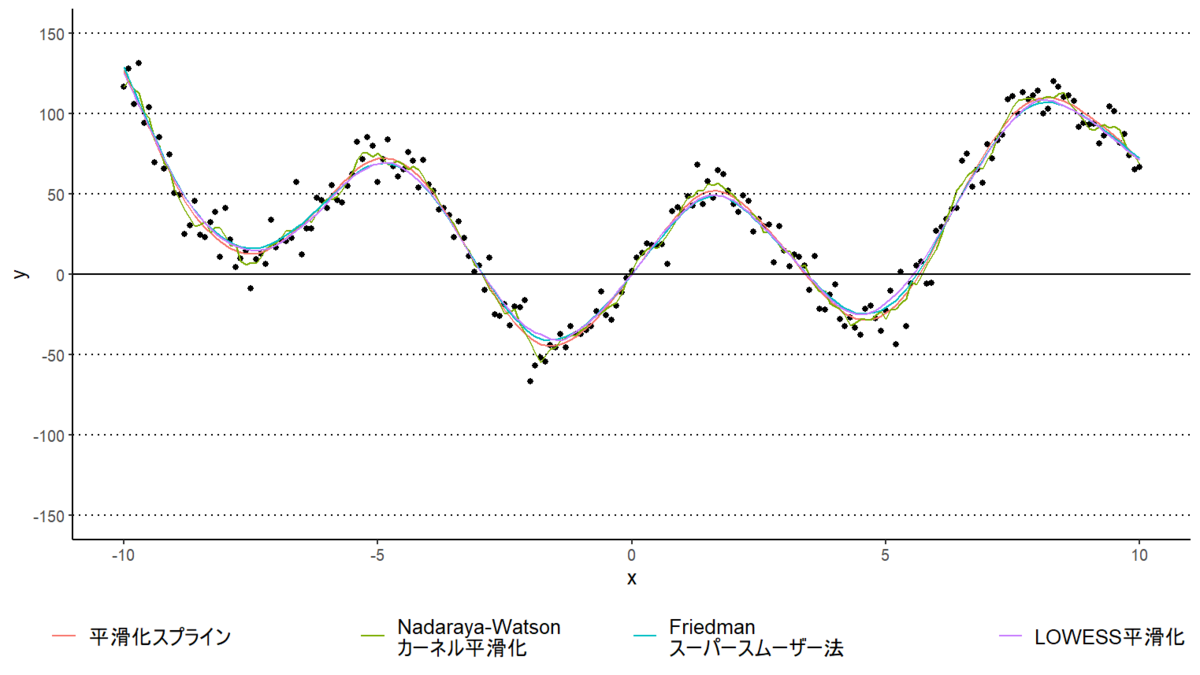

12.5.5　加法モデル

##################
### 加法モデル ###
##################
library("mgcv")

airq2 <- na.exclude(airquality[,1:4]) # 欠損行を除外
airq_gam <- gam(Ozone~s(Solar.R) + s(Wind) + s(Temp), data = airq2)
summary(airq_gam)

補足　スペック情報

エディション	Windows 10 Home
バージョン	20H2
プロセッサ	Intel(R) Core(TM) i5-1035G4 CPU @ 1.10GHz 1.50 GHz
実装 RAM	8.00 GB
システムの種類	64 ビットオペレーティングシステム、x64 ベースプロセッサ
R　バージョン	4.1.3 (March, 2022)
RStudio　バージョン	2022.02.2 Build 485

*1:上記では説明変数をスカラー $x$ としたが、ベクトルでも問題ない。

前回

12. 非線形回帰分析

12.1 ロジスティック回帰

12.2 多項式回帰

12.3 一般化線形モデル

12.4 平滑化回帰と加法モデル

12.5 シミュレーション

12.5.1 ロジスティック回帰

12.5.2 多項式回帰

12.5.3 一般化線形モデル

12.5.4 平滑化回帰

12.5.5 加法モデル

補足 スペック情報