業務でC#を用いることになったので、最近勉強していなくて朧気になってきた知識をReviseする意味でも、以下の書籍を読みながらC#で実装してみる。今回はP.202-204まで。
7. Monte Carloシミュレーション
7.3 オプションの評価
Black-ScholesモデルをMonte Carlo法にて評価する。
株価が幾何ブラウン運動に従うと仮定しよう:
ここでは無リスク金利、
はボラティリティ、
はブラウン運動とする。
本モデルにおいて
とおき、伊藤の公式を適用すべくとおけば
が得られる。伊藤の公式から
が導かれる。この両辺をについて
で積分することで
すなわち
である。以上から
ここでとする。
リスク中立化法により、ペイオフ関数をもつ満期が
のヨーロピアン・オプション価格は
である。ただしはリスク中立確率に関する期待値、
とする。
たとえば、ペイオフ関数がに従うパワー・オプションの価格をMonte Carlo法にて評価しよう。ここでは満期
における株価の分布が既知(
)であるから、
- 正規乱数
を
個生成する。
- 満期
における株価を
とおく。
- デリバティブ価格を以下で与える:
7.4 C#での実装
Box-Muller法の実装結果も併せて掲載する。
7.4.1 コード
using System;
using MathNet.Numerics;
/// <summary>
/// Box-Muller法により正規乱数を生成する
/// </summary>
/// <param name="N">生成したい乱数の数</param>
/// <param name="Mean">乱数が従う分布の平均</param>
/// <param name="Std">乱数が従う分布の標準偏差</param>
/// <returns>N(Mean,Std^2)に従う正規乱数N個</returns>
public static List<double> BoxMuller(int N, double Mean, double Std)
{
var ret = new List<double>();
double[] ret1 = new double[N];
double[] ret2 = new double[N];
var Random = new MathNet.Numerics.Random.MersenneTwister();
Random.NextDoubles(ret1);
Random.NextDoubles(ret2);
double sample = 0.0;
for (int i = 0; i < N; i++)
{
sample = Math.Sqrt(-2.0 * Math.Log(ret1[i])) * Math.Cos(2.0 * Math.PI * ret2[i]);
sample = Std * sample + Mean;
ret.Add(sample);
}
return ret;
}
/// <summary>
/// パワーオプションの価格をMonte Carlo法にて評価する
/// </summary>
/// <param name="S">原資産価格</param>
/// <param name="K">行使価格</param>
/// <param name="r">無リスク金利</param>
/// <param name="T">満期までの期間</param>
/// <param name="std">ボラティリティ</param>
/// <param name="N">シミュレーション回数</param>
/// <returns>パワーオプション価格</returns>
public static double SimPowerOption(int S, int K, double r, double T, double std, int N)
{
double ret = 0.0;
List<double> SimReturn = BoxMuller(N, (r - 0.5 * Math.Pow(std, 2.0)) * T, Math.Pow(std, 2.0) * T);
double Stock = 0.0;
foreach (double Return in SimReturn)
{
Stock = S * Math.Exp(Return);
ret += Math.Pow(Stock - K, 2.0);
}
ret *= Math.Exp(-r * T);
ret /= N;
return ret;
}以上でシミュレーションが可能である。
7.4.2 シミュレーション結果
実際にシミュレーション結果を掲げる。それに当たり、改めて実装対象となる評価式を確認しておこう。
である。ここでである。
このように複数のパラメータが関わることから、各パラメータを動かしつつ前掲したコードでシミュレーションした。なお動かさないパラメータ値は以下の通りである:
パラメータ値 |
刻み |
|
| 初期時点の株価 |
||
| 行使価格 |
||
| 無リスク金利 |
||
| 満期までの年数 |
||
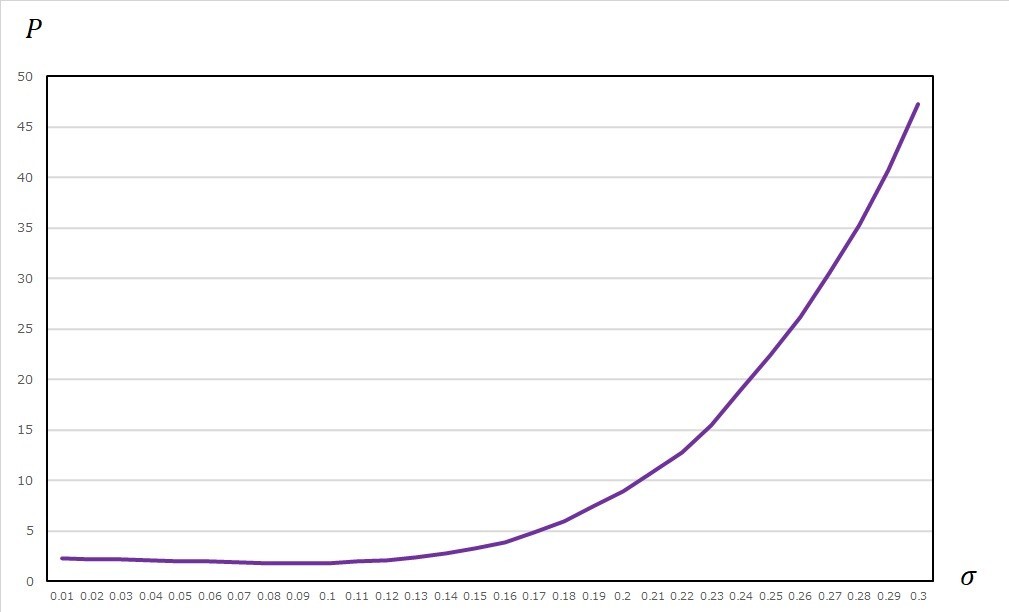
| ボラティリティ |
||
| シミュレーション数 |
図表1 原資産価格

図表3 満期

図表5 シミュレーション回数