金融工学でのモンテカルロ法(08/23)：分散減少法(3) - 「大人の教養・知識・気付き」を伸ばすブログ

　今回から、金融工学におけるシミュレーションについて学んでいく。テキストとして以下を使う。今回はP.69-72まで。

モンテカルロ法の金融工学への応用 (シリーズ現代金融工学)

作者:祥二, 湯前,輝好, 鈴木
朝倉書店

Amazon

power-of-awareness.com

5. 分散減少法
次回

5. 分散減少法

　 $\mathrm{Monte\ Carlo}$ 法は

問題に沿った（同時）分布に従う（多変量）乱数列の生成
その乱数列を使った計算

の2つの部分に分けて考えられる。乱数列の生成は更に

一様分布に従う乱数列 $\{u_1,u_2,\cdots,u_n\}$ の生成
それを元にした必要な同時分布に従う乱数列 $\{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_n\}$ の生成

に分けられる。

　 $\mathrm{Monte\ Carlo}$ 法は高次元問題を取り扱うことはできるものの、誤差を減らすには大きな時間が掛かり時間効率が低い。そこで本章では時間効率を上げるための手段の1つとして分散減少法を説明する。Monte Carlo法における解の統計的誤差は点列数 $N$ に対して $k/\sqrt{N}$ に出来る。分散減少法はこの $k$ を減らす試みである。
　 $\mathrm{Monte\ Carlo}$ 法による関数 $f$ の積分値を

$\begin{aligned} E^{*}[f(X)] \end{aligned}$

と書くことにすると、 $\mathrm{Monte\ Carlo}$ 法のアイディアは以下の2つに分けることが出来ると言える：

関数 $f$ を同じ積分値を取る別の関数に置換え
期待値 $E^{*}[\cdot]$ の取り方を変更

関数 $f$ を同じ積分値を取る別の関数に置換え	*期待値 $E^{}[\cdot]$ の取り方を変更**
(1) 負の相関法	(1) 条件付き $\mathrm{Monte\ Carlo}$ 法
(2) 制御変量法	(2) 層別化法
(3) 回帰分析法	(2-1) ラテン・ハイパーキューブ法
(4) マルチンゲール分散法	(2-2) $\mathrm{Curran}$ の方法
	(3) 加重サンプリング法
	(4) 測度変換法

5.5　制御変量法

　評価対象関数 $f(x)$ から解析的に積分値が既知である関数 $g(x)$ を差し引いた部分に $\mathrm{Monte\ Carlo}$ 法を適用する。そして得られた値に関数 $g$ の理論積分値

$\begin{aligned} m_g=\int_0^1 g(x)dx \end{aligned}$

を加えて解とする。すなわち

$\begin{aligned} \hat{m}_3=\displaystyle{\frac{1}{N}}\sum_{i=1}^{N}\left\{f(\varepsilon_i)-g( (\varepsilon_i) )\right\} + m_g \end{aligned}$

で得られる。
　このとき解の誤差分散は

$\begin{aligned} V\left[\hat{m}_3\right]&=V\left[\displaystyle{\frac{1}{N}}\sum_{i=1}^{N}\left\{f(\varepsilon_i)-g( (\varepsilon_i) )\right\}\right]\\ &=\displaystyle{\frac{1}{N}}V[f(\varepsilon)-g(\varepsilon)]\\ &=\displaystyle{\frac{1}{N}} \left[\int_{0}^{1}\left\{f(X)-g(x)\right\}^2 dx -(m-m_g)^2 \right] \end{aligned}$

となる。
　制御変量法を適用する場合、制御変数の選択が問題となる。ただしオプションの場合は、 $\mathrm{Black}$ - $\mathrm{Scholes}$ 方程式を用いればよい。

5.6　例：算術平均ヨーロピアン・コール・オプションの価格評価

　算術平均ヨーロピアン・コール・オプションの価格を制御変量法で評価する。制御変数は $\mathrm{Black}$ - $\mathrm{Scholes}$ 方程式による解析解を用いる。
　第 $i$ 番目の株価サンプルパスを

$\begin{aligned} \boldsymbol{S}_i&=(S_{i1},\cdots,S_{iM}),\\ S_{ij}&=S_{i(j-1)}+rS_{i(j-1)}\Delta t+\sigma\sqrt{\Delta t}S_{i(j-1)}\xi_{ij},\\ \boldsymbol{\xi}_i&=(\xi_{i1},\cdots,\xi_{iM}),\ \xi_{ij}\sim N(0,1) \end{aligned}$

で発生させる。またペイオフを

$\begin{aligned} A(\boldsymbol{S}_i)=e^{-rT}\max\left[\displaystyle{\frac{1}{M}\sum_{j=1}^{M}S_{ij}}-K,\ 0\right] \end{aligned}$

で与える。このとき、 $\mathrm{Black}$ - $\mathrm{Scholes}$ 方程式に則ったヨーロピアン・コール・オプション価格の解析解を $C_{0}^{BS}(S(t),r,\sigma,T,K)$ とおけば、制御変量法による算術平均ヨーロピアン・コール・オプションの価格の数値解 $\hat{a}$ は

$\begin{aligned} \hat{a}=\displaystyle{\frac{1}{N}}\left[\sum_{i=1}^{N}A(\boldsymbol{S}_i)-C(\boldsymbol{S}_i)\right]+C_{0}^{BS}(S(t),r,\sigma,T,K) \end{aligned}$

で与えられる。したがって

(1)	ある $i$ について互いに独立な標準正規乱数列 $\boldsymbol{\xi}_{i}$ を発生させる。
(2)	株価サンプルパスを $\boldsymbol{S}_i=(S_{i1},\cdots,S_{iM})$ 生成する。
(3)	$A(\boldsymbol{S}_i)-C(\boldsymbol{S}_i)$ を計算する。
(4)	以上を $i=1,\cdots,N$ まで繰り返して $\begin{aligned}\left\{\displaystyle{\frac{1}{N}}\sum_{i=1}^{N}A(\boldsymbol{A}_i)-C(\boldsymbol{A}_i)\right\}\end{aligned}$ を計算する。
(5)	$C_{0}^{BS}(S(t),r,\sigma,T,K)$ を加えて $\hat{a}$ を算出する。

なお負の相関法と制御変量法を併用することも問題ない。その際は、制御変量法を先に適用すればよい。

5.6　5.5.のシミュレーション例

5.6.1　PCスペック情報

エディション	Windows 10 Home
バージョン	20H2
プロセッサ	Intel(R) Core(TM) i5-1035G4 CPU @ 1.10GHz 1.50 GHz
実装 RAM	8.00 GB
システムの種類	64 ビットオペレーティングシステム、x64 ベースプロセッサ
Visual Studio	Microsoft Visual Studio Community 2019 Version 16.8.2
.NET Framework	Version 4.8.04084

5.6.2　コーディング例

　 $1,000$ 回から $100,000$ 回まで $1,000$ 回ずつシミュレーション回数を増やしていったときの通常の $\mathrm{Monte\ Carlo}$ 法と制御変量法の価格パスを調べることとする。

using System;
using System.Collections.Generic;
using System.Linq;
using System.IO;
using System.Text;
using System.Threading.Tasks;
using MathNet.Numerics;

namespace MonteCarlo
{

    /// <summary>
    /// Monte Carlo Simulation
    /// </summary>
    public class MonteCarloSimulation
    {
        /// <summary>
        /// 2つの実数のうち大きい方を返す。
        /// </summary>
        /// <param name="x">実数</param>
        /// <param name="y">実数</param>
        /// <returns>x>=yならばxを、そうでなければyを返す。</returns>
        private static double Max(double x, double y)
        {
            double ret = x + y;
            ret += Math.Abs(x - y);
            ret *= 0.5;
            return ret;
        }

        /// <summary>
        /// Black-Scholes方程式に則ったヨーロピアン・オプション価格を返す。
        /// </summary>
        /// <param name="S">原資産価格</param>
        /// <param name="K">行使価格</param>
        /// <param name="r">無リスク金利</param>
        /// <param name="sigma">ボラティリティ</param>
        /// <param name="T">満期までの期間</param>
        /// <param name="CallPutFlg">コールプットフラグ。0ならばコール、1ならばプットの価格を返す。</param>
        /// <returns>ヨーロピアン・オプションの価格</returns>
        public static double OptionPricing(double S, double K, double r, double sigma, double T, int CallPutFlg)
        {
            if (CallPutFlg == 0 | CallPutFlg == 1)
            {
                double flg = -2.0 * CallPutFlg + 1.0;

                double d = Math.Log(S / K) + (r + 0.5 * Math.Pow(sigma, 2.0)) * T;
                d /= sigma * Math.Sqrt(T);

                double Price = S * MathNet.Numerics.Distributions.Normal.CDF(0.0, 1.0, flg * d);
                Price = flg * Price - flg * K * Math.Exp(-r * T) * MathNet.Numerics.Distributions.Normal.CDF(0.0, 1.0, flg * (d - sigma * Math.Sqrt(T)));

                return Price;
            }
            else
            {
                Console.WriteLine("CallPutFlg must be either 0 or 1.");
                return -99999;
            }
        }

        static void Main(string[] args)
        {
            // 出力先パス
            string OutPath = @"...適当な出力先パス...";

            // オプションの設定
            double S0 = 100;
            double r = 0.02; //年次
            double std = 0.05; //年次
            double K = 80;
            int T = 50; //日数

            // 日次に直す
            r /= 250;
            std /= Math.Sqrt(250);

            // モンテカルロ法の試行回数は変更する
            var TestNum = new List<double>();

            for (int i = 1; i <= 100; i++)
            {
                TestNum.Add(i * 1000);
            }

            var obj = new MathNet.Numerics.Random.MersenneTwister();

            // テスト結果
            List<double> EachResult1 = new List<double>();
            List<double> EachResult2 = new List<double>();

            // 個々の結果
            double SimOP1 = 0.0; // 通常のMonte Carlo法
            double SimOP2 = 0.0; // 制御変数法

            double BSCall = OptionPricing(S0, K, r, std, T, 0);

            Console.WriteLine("Start Simulation Section ...");

            // Test実施
            for (int i = 0; i < TestNum.Count(); i++)
            {
                Console.WriteLine("   Start " + (i + 1) + "/" + TestNum.Count() + "-th test...");

                for (int j = 0; j < TestNum[i]; j++) {
                    Console.WriteLine("   　　Start " + (j + 1) + "/" + TestNum[i] + "-th test...");

                    var StockPath = new List<double>();

                    // 満期までの株価サンプルパスを生成する
                    for (int t = 0; t < T; t++)
                    {
                        if (t == 0)
                        {
                            StockPath.Add(S0);
                        }
                        else
                        {
                            double RN1 = obj.NextDouble();
                            double tmp = (1 + r + std * MathNet.Numerics.Distributions.Normal.InvCDF(0.0, 1.0, RN1)) * StockPath[t - 1];

                            StockPath.Add(tmp);
                        }
                    }

                    //ペイオフを計算
                    double A_S = Math.Exp(-r * T) * Max(StockPath.Average() - K, 0);
                    double C_S = Math.Exp(-r * T) * Max(StockPath.Last() - K, 0);

                    SimOP1 += A_S;
                    SimOP2 += A_S - C_S;
                }

                SimOP1 /= TestNum[i];
                SimOP2 /= TestNum[i];

                SimOP2 += BSCall;

                EachResult1.Add(SimOP1);
                EachResult2.Add(SimOP2);

                // 初期化
                SimOP1 = 0.0;
                SimOP2 = 0.0;
            }


            // 出力
            Console.WriteLine("Start Output Section...");

            string Path = OutPath + "02_MonteCarloEvaluationByEuropeanAverageCallOptionPricing.csv";

            try
            {
                StreamWriter Stream = new StreamWriter(Path, false, Encoding.UTF8);

                Stream.WriteLine(string.Format("No,TestNum, BS, Sim1, Sim2, Abs(Sim1), Abs(Sim2), Rel(Sim1), Rel(Sim2)"));

                for (int i = 0; i < EachResult1.Count(); i++)
                {
                    Stream.WriteLine(string.Format("{0},{1},{2},{3},{4},{5},{6},{7},{8}",
                    i + 1, TestNum[i], BSCall, EachResult1[i], EachResult2[i],
                    Math.Abs(EachResult1[i] - BSCall), Math.Abs(EachResult2[i] - BSCall),
                    Math.Abs(EachResult1[i] - BSCall) / BSCall, Math.Abs(EachResult2[i] - BSCall) / BSCall));
                }

                Stream.Close();
            }
            catch (Exception e)
            {
                Console.WriteLine(e.Message);
            }
        }
    }
}

5.6.3　シミュレーション結果

　シミュレーション結果のグラフは以下の通り：

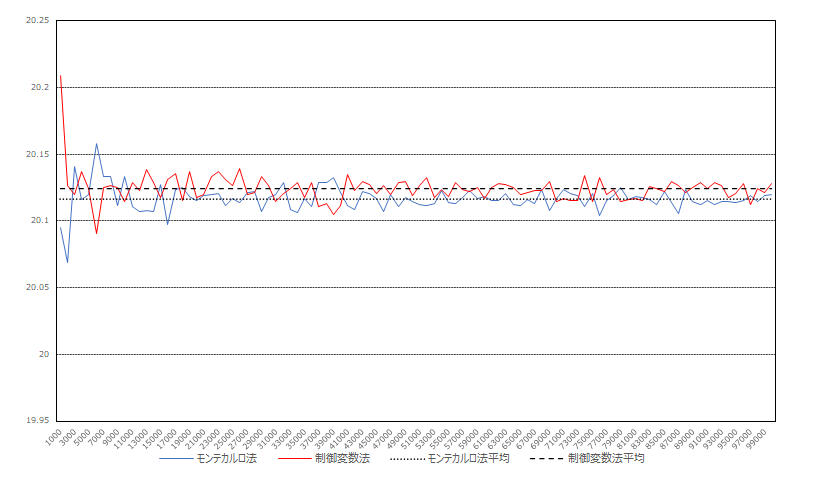
何度か繰り返してみたものの、形状に大きな相違はない。なお通常の $\mathrm{Monte\ Carlo}$ 法はシミュレーション回数が少ないときに平均から大きく逸れているように見えるものの、実質的にはほとんど変わらない。
　通常の $\mathrm{Monte\ Carlo}$ 法と制御変量法とで大きな相違があるとは思えず、むしろ通常の $\mathrm{Monte\ Carlo}$ 法の方が精度が高そうである。ただし平均を取ってみても両者の水準が違う点、回数を増やしても収束が共に遅い点を踏まえると、実装ミスがあるかもしれない。

次回

power-of-awareness.com

5. 分散減少法

5.5 制御変量法

5.6 例：算術平均ヨーロピアン・コール・オプションの価格評価

5.6 5.5.のシミュレーション例

5.6.1 PCスペック情報

5.6.2 コーディング例

5.6.3 シミュレーション結果

次回