Juliaを使ってみる(09/22)：数値積分によるベルヌーイモデルの計算

今回やりたいこと

　確率試行のシミュレーションをJuliaで扱ってみる。

Juliaで作って学ぶベイズ統計学 (KS情報科学専門書)

作者:須山敦志
講談社

Amazon

を参照する。

今回やりたいこと
前回
1.　統計モデリングと推論
- 1.1　数値積分による推論計算
次回

前回

power-of-awareness.com

1.　統計モデリングと推論

1.1　数値積分による推論計算

　数値積分を使って母数の事後分布を計算することもできる。
　まず今回生成してきた過程は、

$\begin{aligned} \mu&\sim U(\mu|0,1),\\ x_1&\sim B(x_1|\mu),\\ x_2&\sim B(x_2|\mu),\\ &\vdots\\ x_n&\sim B(x_n|\mu) \end{aligned}$

で与えることができる。このとき同時分布として書くと、

$\begin{aligned} p(x_1,x_2,\cdots,x_n,\mu)&=p(\mu)p(x_1,\cdots,x_n|\mu)\\ &=p(\mu)\displaystyle{\prod_{i=1}^{n} p(x_i|\mu)}\\ &=p(\mu)p(\boldsymbol{X}|\mu) \end{aligned}$

である。ここで

$\begin{aligned} p(\mu)&=U(\mu|0,1),\\ p(x_n|\mu)&=B(x_n|\mu),i=1,2,\cdots,n \end{aligned}$

である。
　条件付き分布の定義から

$\begin{aligned} p(\mu|\boldsymbol{X})=\displaystyle{\frac{p(\boldsymbol{X}|\mu)p(\mu)}{p(\boldsymbol{X})}} \end{aligned}$

が得られる。
　分子において $p(\boldsymbol{X}|\mu)$ および $p(\mu)$ を計算する必要がある。しかし $p(\boldsymbol{X}|\mu)$ は $\mathrm{Bernoulli}$ 分布の積で $p(\mu)$ は一様分布として与えられる。一方で

$\begin{aligned} p(\boldsymbol{X})=\displaystyle{\int p(\boldsymbol{X}|\mu)p(\mu) d\mu} \end{aligned}$

で計算する。しかしこの右辺の計算はよほどシンプルなモデルを選ばない限り積分計算は困難である。
　新しいデータ $x_p$ に対する予測分布は

$\begin{aligned} p(x_p|\boldsymbol{X})=\displaystyle{\int p(x_p|\mu)p(\mu)d\mu}=\displaystyle{\int\frac{p(x_p|\mu)p(\boldsymbol{X},\mu)}{p(\boldsymbol{X})}d\mu} \end{aligned}$

として計算すればよい。

##########################
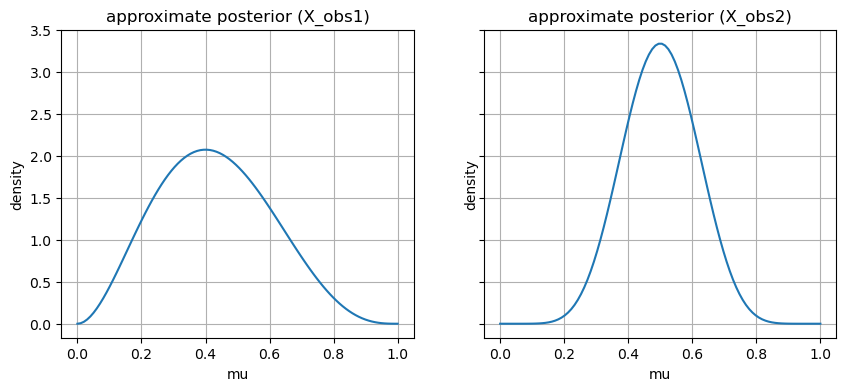
### 事後分布を計算する ###
##########################

using Distributions, PyPlot, LinearAlgebra

# グラフの軸やタイトルを設定する関数
function set_options(ax, xlabel, ylabel, title;
    grid = true, gridy = false, legend = false)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_title(title)
    if grid
        if gridy
            ax.grid(axis = "y")
        else
            ax.grid()
        end
    end
    
    legend && ax.legend()
end


p_joint(X,mu) = prod(pdf.(Bernoulli(mu),X)) * pdf(Uniform(0,1), mu)

# 数値積分
function approx_integration(mu_range, p)
    Delta = mu_range[2]-mu_range[1]
    X -> sum([p(X,mu) * Delta for mu in mu_range]), Delta
end

mu_range = range(0, 1, length =100)


# 数値積分の実行
p_marginal, Delta = approx_integration(mu_range, p_joint)

X_obs1 = [0,0,0,1,1]
X_obs2 = [0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1]

# それぞれの周辺尤度の近似計算
println("$(p_marginal(X_obs1)), $(p_marginal(X_obs2))")

mus =range(0,1, length = 100)
fig, axes = subplots(1, 2, sharey = true, figsize = (10,4))

for (i, X_obs) in enumerate([X_obs1, X_obs2])
    posterior(mu) = p_joint(X_obs, mu) / p_marginal(X_obs)
    axes[i].plot(mus, posterior.(mus))
    set_options(axes[i], "mu", "density", "approximate posterior (X_obs$(i))")
end

### 予測分布を計算
# 積分の中身の式

posterior1(mu) = p_joint(X_obs1, mu) / p_marginal(X_obs1)
posterior2(mu) = p_joint(X_obs2, mu) / p_marginal(X_obs2)
p_inner1(x, mu) = pdf.(Bernoulli(mu), x) * posterior1(mu)
p_inner2(x, mu) = pdf.(Bernoulli(mu), x) * posterior2(mu)

# 母数muに対する積分
mu_range = range(0, 1, length = 100)
pred1, Delta1 = approx_integration(mu_range, p_inner1)
pred2, Delta2 = approx_integration(mu_range, p_inner2)

println("$(pred1(1)), $(pred2(1))")

次回

power-of-awareness.com

今回やりたいこと

前回

1. 統計モデリングと推論

1.1 数値積分による推論計算

次回

1.　統計モデリングと推論

1.1　数値積分による推論計算