Juliaを使ってみる(08/22)：統計モデリングと推論

今回やりたいこと

　確率試行のシミュレーションをJuliaで扱ってみる。

Juliaで作って学ぶベイズ統計学 (KS情報科学専門書)

を参照する。

前回

power-of-awareness.com

1.　統計モデリングと推論

　簡単な統計モデルを構築し、推論を行う。

#######################
### Bernoulliモデル ###
#######################

using Distributions, PyPlot, LinearAlgebra

# グラフの軸やタイトルを設定する関数
function set_options(ax, xlabel, ylabel, title;
    grid = true, gridy = false, legend = false)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_title(title)
    if grid
        if gridy
            ax.grid(axis = "y")
        else
            ax.grid()
        end
    end
    
    legend && ax.legend()
end

# シミュレーションによるサンプルを生成する関数
function generator(N)
    mu = rand(Uniform(0, 1)) # 母数muをランダムに生成
    X = rand(Bernoulli(mu), N) # muを母数とするベルヌーイ乱数をN個生成する
    mu, X # 出力
end

# 5回コイン投げを行う試行を1回実施する
println(generator(5))

# Bernoulli乱数を表・裏で表現してみる
side(x) = x == 1 ? "表" : "裏"

# 5回コイン投げを行う試行を10回実施する
for i in 1:10
    mu, X = generator(5)
    println("コイン$(i), 表が出る確率$(mu), 出た目X = $(side.(X))")
end

2.　伝承サンプリング

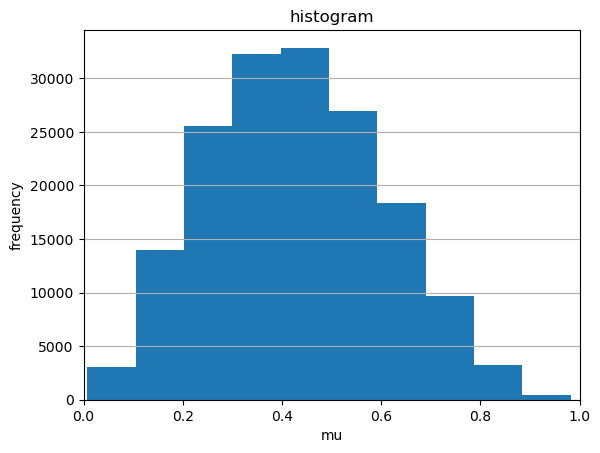
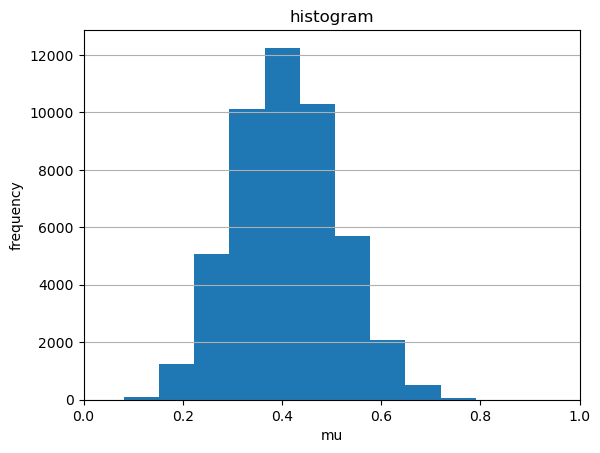
　観測値が得られたときにあり得る母数(上述の)はいくつもあり得る。これを示すべく、おなじ表が出る割合をもつ観測値およびについて伝承サンプリングしてみると、母数の分布は大きく異なっていることが分かる。すなわち何度も偏りをもつコインとそれを用いて面を生成し、現実の観測値と合致した場合のを確保するという試行を何度も行った場合の母数の分布を調べてみる。
　シミュレーションで得られた母数の分布を母数の事後分布と呼ぶ。最初に設定したに関する一様分布は事前分布と呼ばれる。

########################
### 伝承サンプリング ###
########################

using Distributions, PyPlot, LinearAlgebra

# X_obs1
X_obs1 = [0,0,0,1,1] # 観測値

# この場合、mu=0.5,0.4,0.3のいずれもあり得る
# 伝承サンプリングでmuの傾向性を考える

maxiter = 1000000
mu_posterior1 = [] # サンプルを得た後のmuを格納

for i in 1:maxiter
    mu, X = generator(length(X_obs1))
    
    sum(X) == sum(X_obs1) && push!(mu_posterior1,mu)
end

acceptance_rate = length(mu_posterior1)/maxiter
println("acceptance_rate = $(acceptance_rate)")

mu_posterior1'

fig, ax = subplots()
ax.hist(mu_posterior1)
ax.set_xlim([0,1])
set_options(ax,"mu", "frequency", "histogram"; gridy = true)

# X_obs2
X_obs2 = [0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1]


# この場合、mu=0.5,0.4,0.3のいずれもあり得る
# 伝承サンプリングでmuの傾向性を考える

maxiter = 1000000
mu_posterior2 = [] # サンプルを得た後のmuを格納

for i in 1:maxiter
    mu, X = generator(length(X_obs2))
    
    sum(X) == sum(X_obs2) && push!(mu_posterior2,mu)
end

acceptance_rate = length(mu_posterior2)/maxiter
println("acceptance_rate = $(acceptance_rate)")

mu_posterior2'

fig, ax = subplots()
ax.hist(mu_posterior2)
ax.set_xlim([0,1])
set_options(ax,"mu", "frequency", "histogram"; gridy = true)

pred1 = mean(rand.(Bernoulli.(mu_posterior1)))
pred2 = mean(rand.(Bernoulli.(mu_posterior2)))

println("$(pred1),$(pred2)")

　このように事後分布を考慮すると、コインの表裏の比率のみならず全試行回数も考慮に入れることができる。

　予測が相違したのは、事前分布が相違することによる。

3.　事前分布の変更

　たとえばということが分かっているとする。

#################################################
### 事前情報として0<mu<=0.5が分かっている場合 ###
#################################################

using Distributions

function generator2(N)
    mu = rand(Uniform(0,0.5))
    X = rand(Bernoulli(mu), N)
    mu, X
end

for i in 1:10
    mu, X = generator2(5)
    println("コイン$(i), 表が出る確率mu=$(mu), 出目X = $(side.(X))")
end

次回

power-of-awareness.com