1. ロジスティック回帰
ロジスティック回帰は2値を取り得るため、まずはその2値を表現するのに分布を用いることにする。その
分布の確率パラメータ
の定式化を次に考える。ここでは
としたいが、そうすると実数全体を取り得るため、シグモイド関数を用いることとする。すなわち
で与えられる。
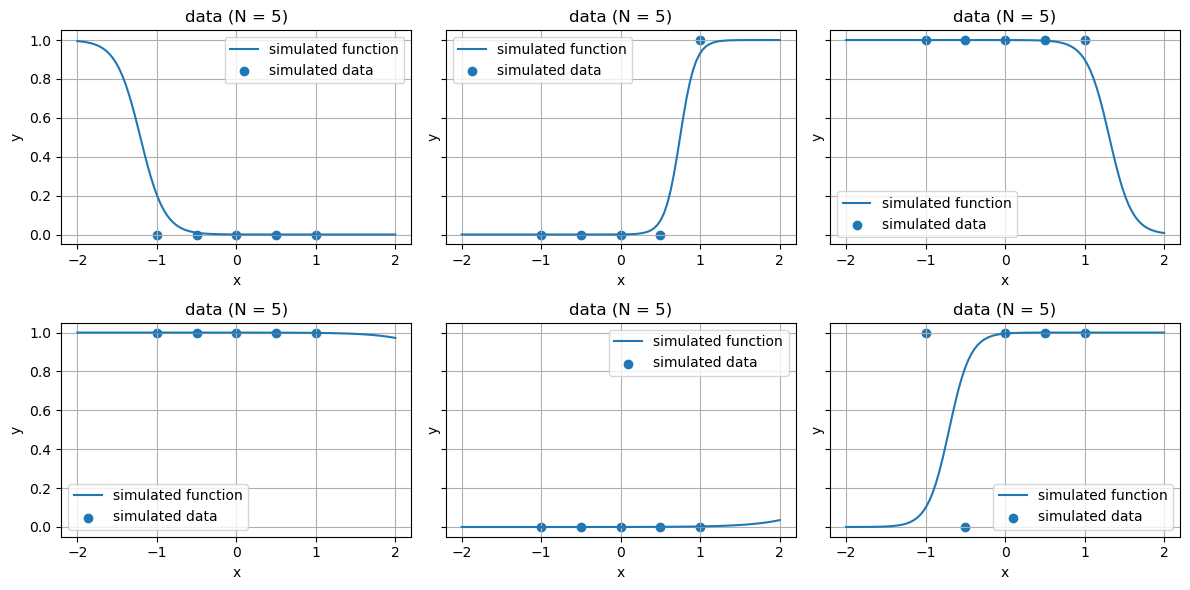
########################## ### ロジスティック回帰 ### ########################## using Distributions using PyPlot # グラフの諸設定を行う関数 function set_options(ax, xlabel, ylabel, title; grid = true, gridy = false, legend = false) ax.set_xlabel(xlabel) ax.set_ylabel(ylabel) ax.set_title(title) if grid if gridy ax.grid(axis = "y") else ax.grid() end end legend && ax.legend() end ### sig(x)= 1/(1+exp(-x)) # パラメータ、関数、出力集合Yを生成 function generate_logistic(X, μ₁,μ₂,σ₁,σ₂) w₁ = rand(Normal(μ₁,σ₁)) w₂ = rand(Normal(μ₂,σ₂)) f(x) = sig(w₁*x+w₂) Y = rand.(Bernoulli.(f.(X))) Y, f, w₁, w₂ end # パラメータ μ₁ = 0 μ₂ = 0 σ₁ = 10.0 σ₂ = 10.0 X = [-1.0,-0.5,0,0.5,1.0] xs = range(-2, 2, length = 100) fig, axes = subplots(2, 3, sharey = true, figsize = (12,6)) for ax in axes # 関数f,出力Yの生成 Y, f, w₁, w₂ = generate_logistic(X,μ₁,μ₂,σ₁,σ₂) # 生成された直線とYのプロット ax.plot(xs, f.(xs), label = "simulated function") ax.scatter(X, Y, label = "simulated data") set_options(ax, "x", "y", "data (N = $(length(X)))", legend = true) end tight_layout()
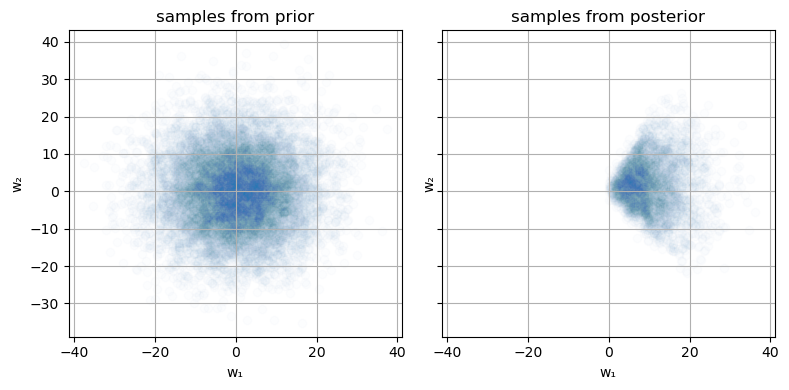
2.1 伝承サンプリング
###################################### ### 伝承サンプリングによる事後分布 ### ###################################### ### 観測データ X_obs = [-2,1,2] Y_obs = Bool.([0, 1, 1]) fig,ax = subplots() ax.scatter(X_obs, Y_obs) ax.set_xlim([-3,3]) set_options(ax, "x", "y", "data (N = $(length(X_obs)))") ### 事後分布 # 最大サンプリング数 maxiter = 10_000 # パラメータ(保存用) param_posterior = Vector{Tuple{Float64, Float64}}() for i in 1:maxiter # 関数f,出力Yの生成 Y, f, w₁, w₂ = generate_logistic(X_obs, μ₁, μ₂, σ₁, σ₂) # 観測データと一致していれば、そのときのパラメータwを保存 Y == Y_obs && push!(param_posterior, (w₁,w₂)) end # 標本受容率 acceptance_rate = length(param_posterior) / maxiter println("acceptance rate = $(acceptance_rate)") # パラメータ抽出用の関数 unzip(a) = map(x -> getfield.(a, x), fieldnames(eltype(a))) # 事前分布からのサンプル param_prior = [generate_logistic(X, μ₁, μ₂, σ₁,σ₂)[3:4] for i in 1:10_000] w₁_prior, w₂_prior = unzip(param_prior) # 事後分布からのサンプル w₁_posterior, w₂_posterior = unzip(param_posterior) fig, axes = subplots(1, 2, sharex = true, sharey = true, figsize = (8, 4)) # 事前分布 axes[1].scatter(w₁_prior,w₂_prior, alpha = 0.01) set_options(axes[1], "w₁", "w₂", "samples from prior") # 事後分布 axes[2].scatter(w₁_posterior,w₂_posterior, alpha = 0.01) set_options(axes[2], "w₁", "w₂", "samples from posterior") tight_layout()
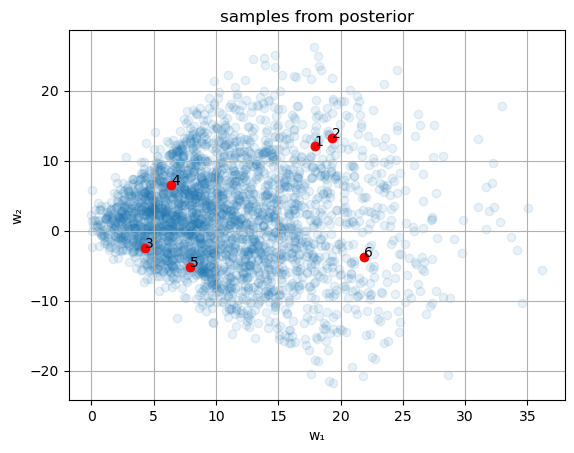
# 関数を可視化する範囲 xs = range(-3, 3, length = 100) # サンプリングで得られたパラメータ全体のプロット fig, ax = subplots() ax.scatter(w₁_posterior, w₂_posterior, alpha = 0.1) set_options(ax, "w₁", "w₂", "samples from posterior") fig,axes = subplots(2, 3, figsize = (12, 8)) for i in eachindex(axes) # 関数を可視化するためのwを取得 j = round(Int, length(param_posterior) * rand()) + 1 w₁,w₂ = param_posterior[j] # 選択されたw ax.scatter(w₁, w₂, color = "r") ax.text(w₁, w₂, i) # 対応する関数のプロット f(x) = sig(w₁ * x + w₂) axes[i].plot(xs, f.(xs), "r") # 観測データのプロット axes[i].scatter(X_obs, Y_obs) axes[i].set_ylim([-0.1, 1.1]) set_options(axes[i], "x", "y(prob.)", "($(i)) w₁ = $(round(w₁, digits = 3)), w₂ = $(round(w₂, digits = 3))") end tight_layout()
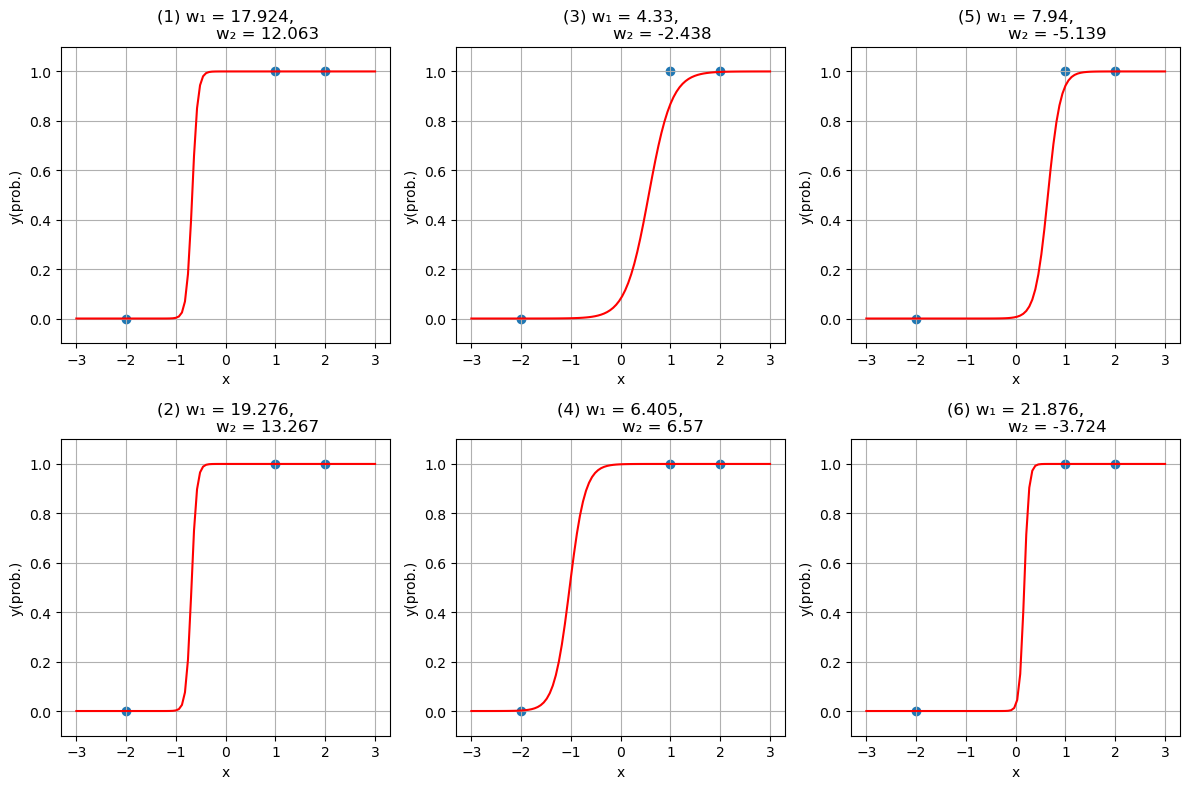
2.2 予測分布のプロット
fig, axes = subplots(1, 2, sharey = true, figsize = (12, 4)) fs = [] for (i, param) in enumerate(param_posterior) # 1サンプル分のパラメータ w₁, w₂ = param # 1サンプル分の予測関数 f(x) = sig(w₁ * x + w₂) axes[1].plot(xs, f.(xs), "g", alpha = 0.01) push!(fs, f.(xs)) end axes[1].scatter(X_obs, Y_obs) set_options(axes[1], "x", "y(Prob.)", "function samples") # 予測確率 axes[2].plot(xs, mean(fs), label = "prediction") axes[2].scatter(X_obs, Y_obs, label = "data") set_options(axes[2], "x", "y(Prob.)", "prediction", legend = true) tight_layout()
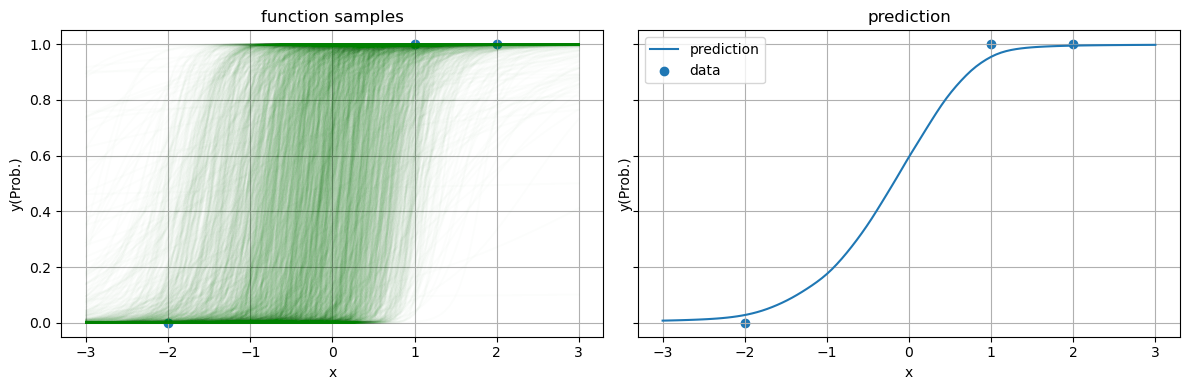
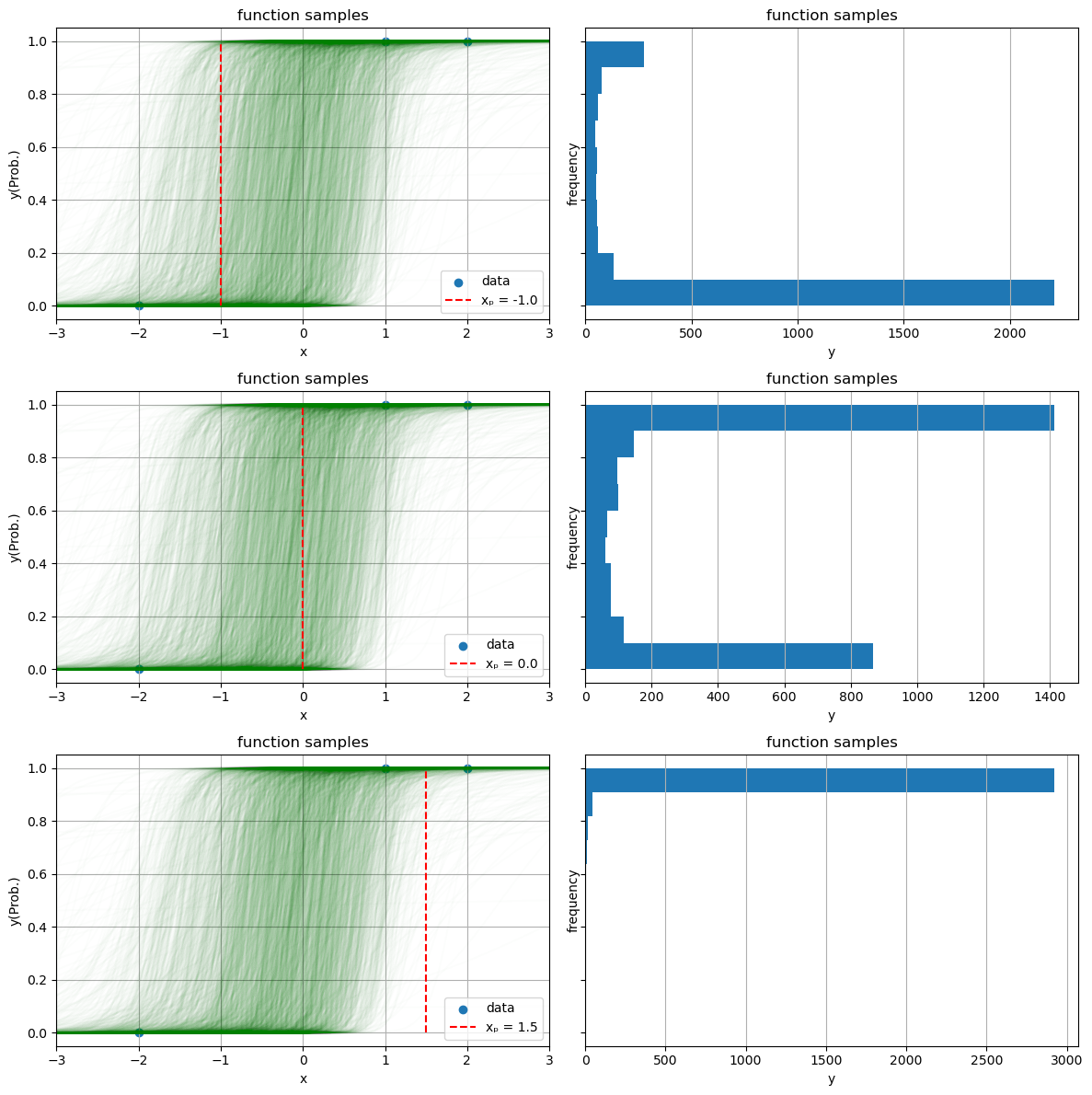
2.3 特定の点の予測値
# 予測対象の点候補 x_list = [-1.0, 0.0, 1.5] fig_num = length(x_list) fig,axes = subplots(fig_num, 2, sharey = true, figsize = (12, 4 * fig_num)) for (j, x) in enumerate(x_list) # パラメータごとに関数を可視化 for (i, param) in enumerate(param_posterior) w₁, w₂ = param f(x) = sig(w₁*x+w₂) axes[j].plot(xs, f.(xs), "g", alpha = 0.01) end # 観測値 axes[j].scatter(X_obs, Y_obs, label = "data") # 候補点のx座標 axes[j].plot([x,x],[0,1], "r--", label = "xₚ = $(x)") axes[j].set_xlim(extrema(xs)) set_options(axes[j], "x", "y(Prob.)", "function samples") axes[j].legend(loc = "lower right") # 点xにおける関数値をヒストグラムとして可視化 probs = [sig(param[1] * x + param[2]) for param in param_posterior] axes[j + fig_num].hist(probs, orientation = "horizontal") set_options(axes[j + fig_num], "y", "frequency", "function samples", grid = false) axes[j + fig_num].grid(axis = "x") end tight_layout()