1. 状態空間モデル
各データ間に時間的依存性があると想定できる場合に有用なモデルとして状態空間モデルを導入する。
状態変数と呼ばれる潜在変数に関して、
連鎖を与える。すなわち、
と仮定し、更にこうして数珠上に生成された潜在変数に基づき観測データ
が独立に
と生成されるとも仮定する*1。
2. 実装
2.1 スムージング
ここでは2次元のデータ系列から背後に存在すると考えられる状態変数
を抽出することを考える。すなわち
という事後分布を計算する*2。
###################### ### 状態空間モデル ### ###################### using Distributions, PyPlot, ForwardDiff, LinearAlgebra eye(n) = Diagonal{Float64}(I, n) # グラフの諸設定を行う関数 function set_options(ax, xlabel, ylabel, title; grid = true, gridy = false, legend = false) ax.set_xlabel(xlabel) ax.set_ylabel(ylabel) ax.set_title(title) if grid if gridy ax.grid(axis = "y") else ax.grid() end end legend && ax.legend() end ### Hamiltonia Monte Carlo # Hamiltonian Monte Carlo method function HMC(log_p_tilde, μ₀; maxiter::Int64, L::Int64, ε::Float64) # leapfrog による値の更新 function leapflog(grad, p_in,μ_in, L, ε) μ=μ_in p = p_in + 0.5 *ε*grad(μ) for l in 1: L-1 μ +=ε*p p += ε*grad(μ) end μ += ε*p p += 0.5 *ε*grad(μ) p, μ end # 非正規化対数事後分布の勾配関数 grad(μ) = ForwardDiff.gradient(log_p_tilde, μ) # サンプルを格納する配列 D = length(μ₀) μ_samples = Array{typeof(μ₀[1]), 2}(undef, D, maxiter) # 初期サンプル μ_samples[:, 1] = μ₀ # 受容されたサンプル数 num_accepted = 1 for i in 2:maxiter # 運動量の生成 p_in = randn(size(μ₀)) # リープフロッグ p_out, μ_out = leapflog(grad, p_in, μ_samples[:, i-1], L, ε) # 比率rの対数を計算 μ_in = μ_samples[:, i-1] log_r = (log_p_tilde(μ_out) + logpdf(MvNormal(zeros(D),eye(D)), vec(p_out))) - (log_p_tilde(μ_in) + logpdf(MvNormal(zeros(D),eye(D)),vec(p_in))) # 確率rでサンプル受容 is_accepted = min(1, exp(log_r)) > rand() new_sample = is_accepted ? μ_out : μ_in # 新サンプルを格納 μ_samples[:,i] = new_sample # 受容された場合、合計を加算する num_accepted += is_accepted end μ_samples, num_accepted end function inference_wrapper_HMC(log_joint, params, w_init; maxiter::Int64 = 100_000, L::Int64 = 100, ε::Float64 = 1e-1) ulp(w) = log_joint(w, params...) HMC(ulp, w_init; maxiter = maxiter, L = L, ε = ε) end ### 観測データの設定 # 系列の長さ n = 20 # 観測データの次元 D = 2 # 系列データ Y_obs = [1.9 0.2 0.1 1.4 0.3 1.3 1.6 1.5 1.6 2.4 #= =# 1.7 3.6 2.8 1.6 3.0 2.8 5.1 5.2 6.0 6.4; 0.1 0.2 0.9 1.5 4.0 5.0 6.3 5.8 6.4 7.5 #= =# 6.7 7.6 8.7 8.2 8.5 9.6 8.4 8.4 8.4 9.0] # 2次元に系列データを可視化 fig, ax = subplots(figsize = (6,6)) ax.plot(Y_obs[1,:], Y_obs[2,:], "kx--") ax.text(Y_obs[1,1], Y_obs[2,1], "start", color = "r") ax.text(Y_obs[1,end], Y_obs[2,end], "goal", color = "r") set_options(ax,"y₁", "y₂", "2dim data") # 初期状態へ与えるノイズの散らばり σ₁ = 100.0 # 状態遷移に仮定するノイズの散らばり σ_x = 1.0 # 観測値に仮定するノイズの散らばり σ_y = 1.0 # 状態の遷移系列に関する対数密度関数 @views transition(X, σ₁, σ_x, D, n) = logpdf(MvNormal(zeros(D), σ₁*eye(D)), X[:,1]) + sum([logpdf(MvNormal(X[:, i-1], σ_x * eye(D)), X[:, i]) for i in 2:n]) # 観測データに関する対数密度 @views observation(X, Y, σ_y, D, n) = sum([logpdf(MvNormal(X[:,i], σ_y * eye(D)),Y[:,i]) for i in 2:n]) # 対数同時分布 log_joint_tmp(X, Y, σ₁, σ_x, σ_y, D, n) = transition(X, σ₁, σ_x, D, n) + observation(X, Y, σ_y, D, n) # Dn次元ベクトルを入力とした関数として定義する log_joint(X_vec, Y, σ₁, σ_x, σ_y, D, n) = log_joint_tmp(reshape(X_vec, D, n), Y, σ₁, σ_x, σ_y, D, n) params = (Y_obs, σ₁, σ_x, σ_y, D, n) # 非正規化対数事後分布 ulp(X_vec) = log_joint(X_vec, params...) # 初期値 X_init = randn(D * n) # 標本サイズ maxiter = 1000 # HMCの実行 samples, num_accepted = inference_wrapper_HMC(log_joint, params, X_init, maxiter = maxiter) println("acceptance rate = $(num_accepted/maxiter)") fig, ax = subplots(figsize=(6,6)) for i in 1:maxiter X = reshape(samples[:,i], 2, n) ax.plot(X[1,:], X[2,:], "go--", alpha = 10.0 / maxiter) end # 観測データの可視化 ax.plot(Y_obs[1,:], Y_obs[2,:], "kx--", label = "observation (Y)") # 状態変数の平均 mean_trace = reshape(mean(samples, dims = 2), 2, n) ax.plot(mean_trace[1,:], mean_trace[2,:], "ro--", label = "estimate_posistion (X)") set_options(ax,"y₁","y₂", "2-dim data", legend = true)
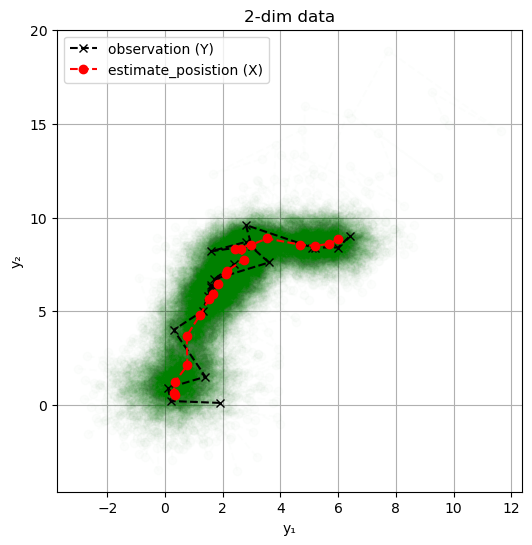
なおここでの方法は状態全体としても多変量正規分布であるため、解析的にも得ることができる。より効率的に厳密解を得るためにはカルマンフィルタなどが用いられる。
2.2 回帰への適用
状態空間モデルは回帰に応用できる。ある入力値と出力値の組について、背後に経時的な変化成分
が存在すると仮定する。モデルの同時分布は
とする。ただしここでは
とした。
###################### ### 状態空間モデル ### ###################### using Distributions, PyPlot, ForwardDiff, LinearAlgebra eye(n) = Diagonal{Float64}(I, n) # グラフの諸設定を行う関数 function set_options(ax, xlabel, ylabel, title; grid = true, gridy = false, legend = false) ax.set_xlabel(xlabel) ax.set_ylabel(ylabel) ax.set_title(title) if grid if gridy ax.grid(axis = "y") else ax.grid() end end legend && ax.legend() end ### Hamiltonia Monte Carlo # Hamiltonian Monte Carlo method function HMC(log_p_tilde, μ₀; maxiter::Int64, L::Int64, ε::Float64) # leapfrog による値の更新 function leapflog(grad, p_in,μ_in, L, ε) μ=μ_in p = p_in + 0.5 *ε*grad(μ) for l in 1: L-1 μ +=ε*p p += ε*grad(μ) end μ += ε*p p += 0.5 *ε*grad(μ) p, μ end # 非正規化対数事後分布の勾配関数 grad(μ) = ForwardDiff.gradient(log_p_tilde, μ) # サンプルを格納する配列 D = length(μ₀) μ_samples = Array{typeof(μ₀[1]), 2}(undef, D, maxiter) # 初期サンプル μ_samples[:, 1] = μ₀ # 受容されたサンプル数 num_accepted = 1 for i in 2:maxiter # 運動量の生成 p_in = randn(size(μ₀)) # リープフロッグ p_out, μ_out = leapflog(grad, p_in, μ_samples[:, i-1], L, ε) # 比率rの対数を計算 μ_in = μ_samples[:, i-1] log_r = (log_p_tilde(μ_out) + logpdf(MvNormal(zeros(D),eye(D)), vec(p_out))) - (log_p_tilde(μ_in) + logpdf(MvNormal(zeros(D),eye(D)),vec(p_in))) # 確率rでサンプル受容 is_accepted = min(1, exp(log_r)) > rand() new_sample = is_accepted ? μ_out : μ_in # 新サンプルを格納 μ_samples[:,i] = new_sample # 受容された場合、合計を加算する num_accepted += is_accepted end μ_samples, num_accepted end function inference_wrapper_HMC(log_joint, params, w_init; maxiter::Int64 = 100_000, L::Int64 = 100, ε::Float64 = 1e-1) ulp(w) = log_joint(w, params...) HMC(ulp, w_init; maxiter = maxiter, L = L, ε = ε) end # 観測データ数 n = 20 # 入力データ Z_obs = [10,10,10,10,10,10,10,10,10,15, 15,15,15,15,15,15,8,8,8,8] # 出力データ Y_obs = [67,64,60,60,57,54,51,51,49,63, 62,62,58,57,53,51,24,22,23,19] ## 散布図 fig,ax = subplots() ax.scatter(Z_obs, Y_obs) set_options(ax, "z", "y", "data(scatter)") fig, axes = subplots(2,1,figsize = (8,6)) # 出力値 axes[1].plot(Y_obs) set_options(axes[1], "time", "y", "time series(Y_obs)") # 入力値 axes[2].plot(Z_obs) set_options(axes[2], "time", "z", "time series(Z_obs)") tight_layout() # 初期状態へ与えるノイズの散らばり σ₀ = 10.0 # 状態遷移に仮定するノイズの散らばり σ_x = 1.0 # 観測値に仮定するノイズの散らばり σ_y = 0.5 # 母数に仮定するノイズの散らばり σ_w = 100.0 # 母数の事前分布 prior(w,σ_w) = logpdf(MvNormal(zeros(2), σ_w*eye(2)),w) # 状態の遷移系列に関する対数密度 @views transition(X, σ₀, σ_x) = logpdf(Normal(0, σ₀), X[1]) + sum(logpdf.(Normal.(X[1:n-1], σ_x), X[2:n])) # 観測値に関する対数密度 @views observation(X,Y,Z,w) = sum(logpdf.(Normal.(w[1] * Z .+ w[2] + X, σ_y), Y)) # 対数同時分布 log_joint_tmp(X, w, Y, Z,σ_w, σ_0, σ_x) = transition(X, σ₀, σ_x) + observation(X, Y, Z, w) + prior(w₁, σ_w) @views log_joint(X_vec, Y, Z,σ_w, σ₀, σ_x) = transition(X_vec[1:n], σ₀, σ_x) + observation(X_vec[1:n], Y, Z, X_vec[n+1:n+2]) + prior(X_vec[n+1:n+2], σ_w) params = (Y_obs, Z_obs, σ_w, σ₀, σ_x) ### HMC x_init = randn(n+2) maxiter = 1000 samples, num_accepted = inference_wrapper_HMC(log_joint, params, x_init, maxiter = maxiter, L = 100, ε = 1e-2) println("acceptance rate = $(num_accepted/maxiter)") # 推定結果の可視化 fig, axes = subplots(5, 1, figsize = (8, 15)) # 出力値 axes[1].plot(Y_obs) set_options(axes[1], "time", "y", "output data (Y)") # 入力値 axes[2].plot(Z_obs) set_options(axes[2], "time", "z", "output data (Z)") # 回帰の説明分 for i in 1:maxiter w₁, w₂ = samples[[n+1,n+2], i] axes[3].plot(w₁ * Z_obs .+ w₂, "g", alpha = 10/maxiter) end set_options(axes[3], "time", "w₁z + w₂", "regression") # 状態変数の説明分 for i in 1:maxiter X = samples[1:n, i] axes[4].plot(X, "g", alpha = 10/maxiter) end set_options(axes[4], "time", "x", "time series") # 回帰と状態変数の和 for i in 1:maxiter w₁, w₂ = samples[[n+1,n+2], i] X = samples[1:n, i] axes[5].plot(w₁*Z_obs .+ w₂ + X, "g", alpha = 10/maxiter) end set_options(axes[5], "time", "w₁z + w₂ + x", "regression + time series", legend = true) tight_layout()

