効果検証入門（06/08） - 「大人の教養・知識・気付き」を伸ばすブログ

　計量経済学の知見をより深めるべく

効果検証入門〜正しい比較のための因果推論／計量経済学の基礎

作者:安井翔太
技術評論社

Amazon

を基に因果推論と計量経済学を学んでいく。

前回

power-of-awareness.com

前回
4.　傾向スコアを用いた分析
- 4.5　LaLonde(1986)を用いた実証分析
今回のまとめ
次回

4.　傾向スコアを用いた分析

　回帰分析では共変量の選定が重要だが、それは同時に難しい過程である。実際の分析では目的変数 $Y$ がどのような仕組みで決定されているかについて不充分な情報しか得られない場合がある。また目的変数と説明変数との関係として線形・非線形の決定も同様に難しい。推定される効果も標本の特徴で介入変数の効果が変わり得る場合に推定される効果の性質が異なるという問題がある。
　これから議論する傾向スコアは各標本において介入が行われる確率を表す。傾向スコアを用いた分析は介入が行われた仕組みに注目し、介入グループと非介入グループのデータの性質を似せる操作を行うことで、上記問題点を回避させるような方法である。
　CIAではモデルに利用されている共変量 $\boldsymbol{X}_i$ の値が同じ標本の中で介入が $Y^{(0)}$ とは独立に割り振られていることを示していた。このとき　共変量 $\boldsymbol{X}_i$ の値が同じ標本の間において介入はランダムに割り振られている状態に等しいため、効果を推定可能であった。これに対して傾向スコアは介入が割り振られる確率である。傾向スコア $P(X_i)$ が同一になるような標本の中では介入が $Y^{(0)}$ とは独立に割り振られているという仮定に基づいている。したがって共変量から算出した介入の割り振り確率で条件づけた標本の中で介入の割り振りが独立だと考える点が、傾向スコアと回帰分析による推定との差異である。

4.5　LaLonde(1986)を用いた実証分析

　 $\mathrm{RCT}$ による実験結果を因果推論手法を用いてどの程度できるかを $\mathrm{LaLonde(1986)}$ のデータを用いて検証する。
　 $\mathrm{NSW}$ ( $\mathrm{National\ Supported\ Work}$ )と呼ばれる1970年代に実施された実験のデータを用いる。 $\mathrm{NSW}$ は労働市場へ参加できないような人々に、カウンセリングおよび9～18か月の就労経験を与えることで就職支援を行う制度である。
　 $\mathrm{LaLonde(1986)}$ では、　 $\mathrm{NSW}$ で得られたデータから非介入グループを削除し、代わりに実験の外で得られた $\mathrm{CPS}$ （ $\mathrm{Current\ Population\ Survey}$ ）という調査データを代わりに挿入したデータセットを作成した。これにより、

$\mathrm{NSW}$ による $\mathrm{RCT}$ の効果を知りつつも、
$\mathrm{CPS}$ でわざと選択バイアスを発生させた

データセットを構築した。

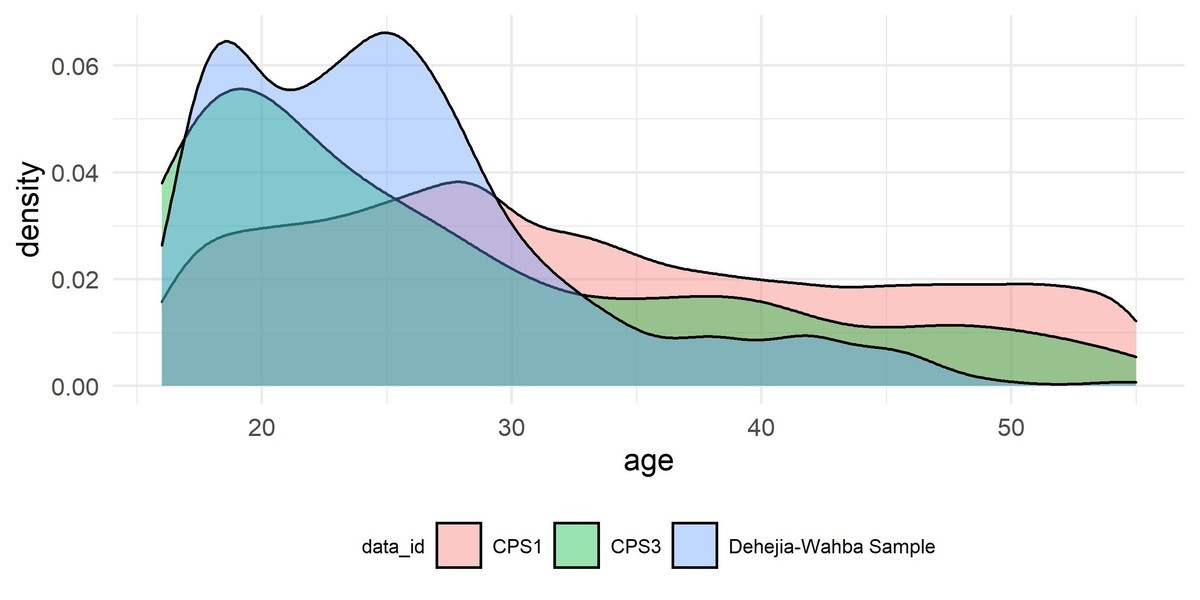
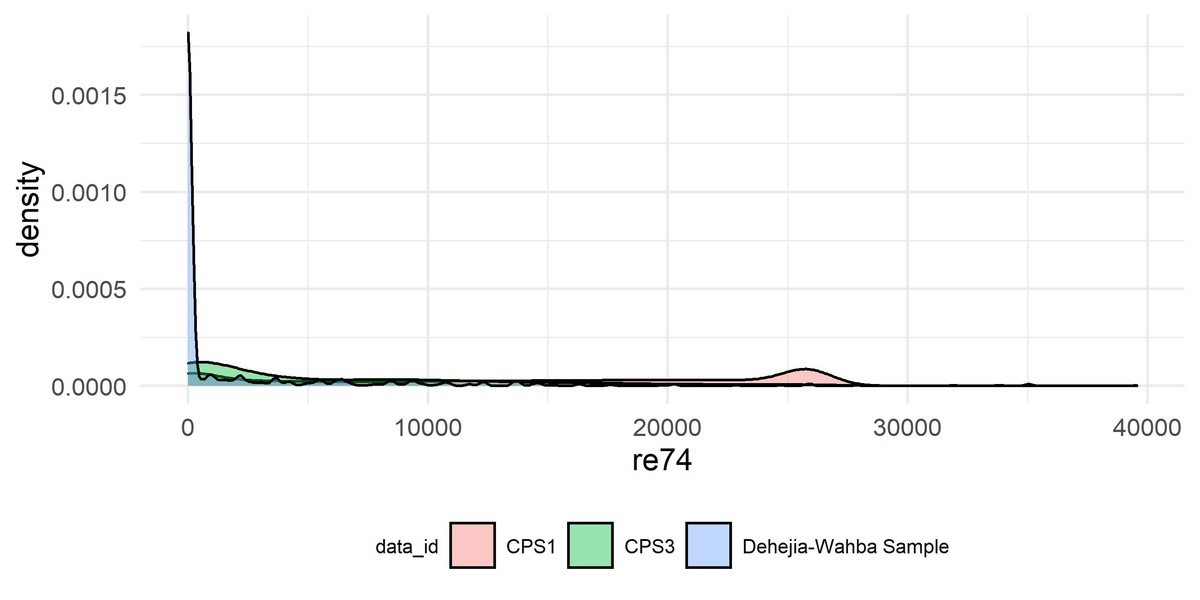
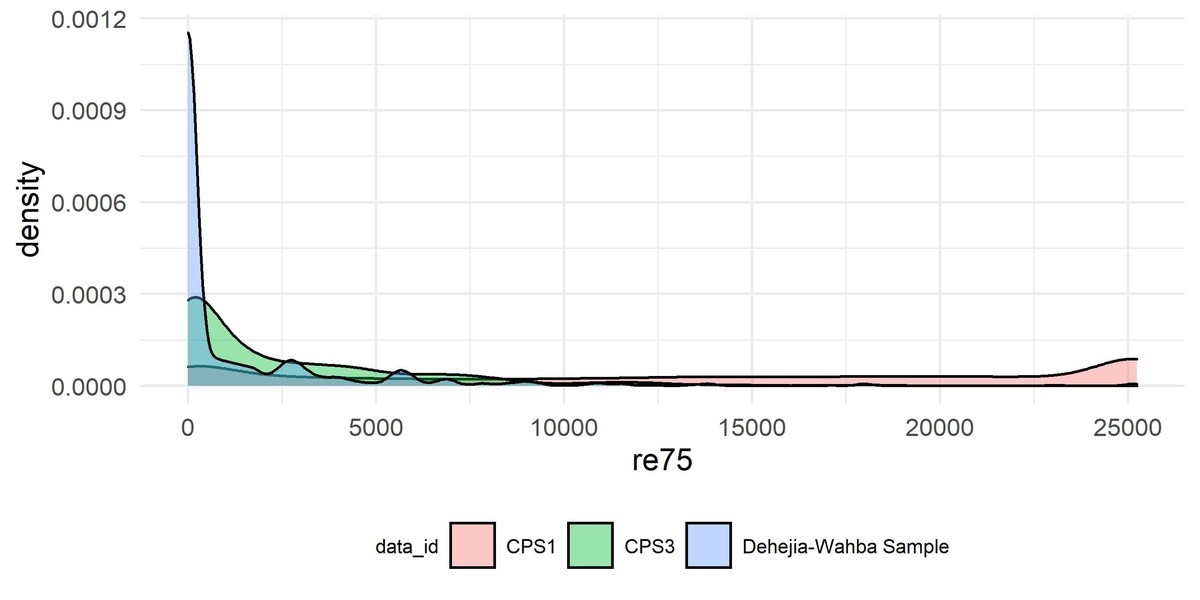
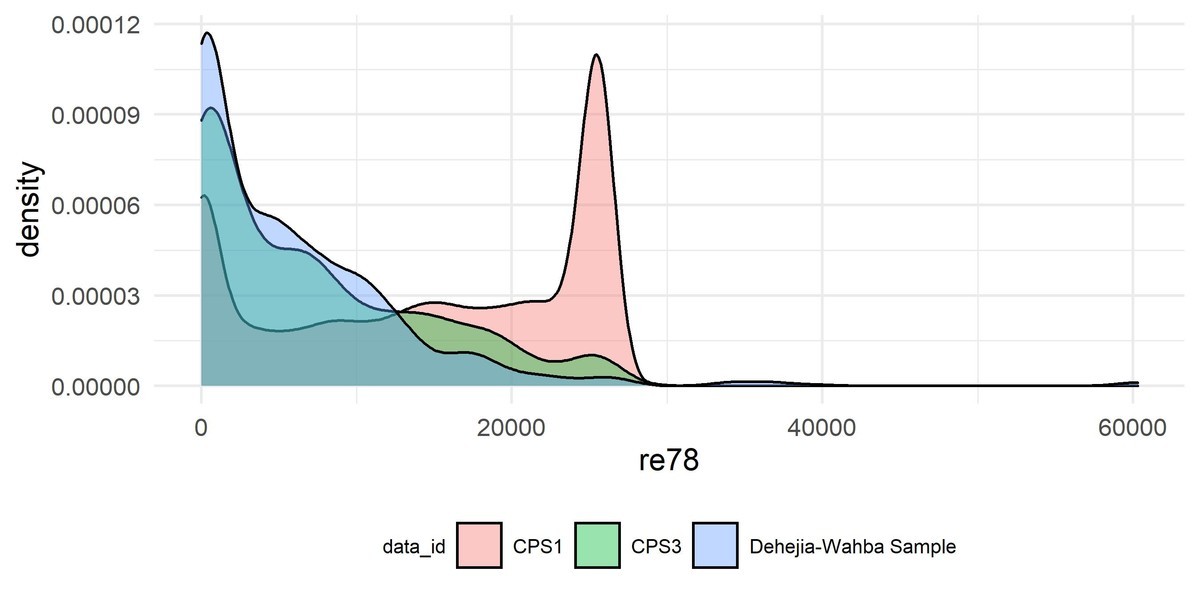
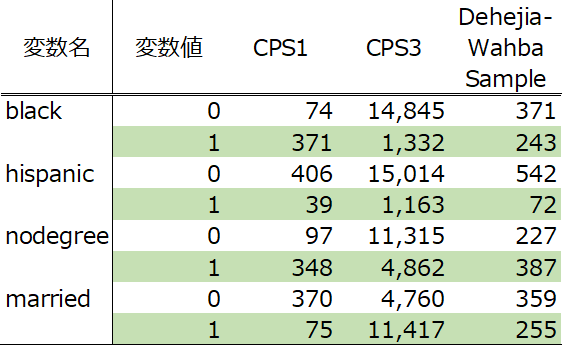
4.5.1　データセット

各変数：

	変数名	内容
	$\mathrm{data}$ _ $\mathrm{id}$	データID
	$\mathrm{earn}_{n}$	ある年( $1974,1975,1978$ )における収入
	$\mathrm{treat}$	介入の有無
	$\mathrm{age}$	年齢
	$\mathrm{education}$	学歴：最終的に学校に通っていた年齢
	$\mathrm{black}$	黒人か否か
	$\mathrm{hispanic}$	ヒスパニックか否か
	$\mathrm{nodegree}$	学位の有無
	$\mathrm{married}$	既婚か非婚か

各変数の分布*1

4.5.2　RCTにおける効果検証

　 $\mathrm{RCT}$ の結果を確認する。ここでは以下の重回帰モデルを想定する。

$\begin{aligned} \mathrm{earn}_{78,i}=&\beta_0+\beta_1\cdot\mathrm{treatment}+\beta_2\cdot\mathrm{earn}_{74,i}+\beta_3\cdot\mathrm{earn}_{75,i}\\ &+\beta_4\cdot\mathrm{age}_{i}+\beta_5\cdot\mathrm{education}_{i}+\beta_6\cdot\mathrm{black}_{i}\\ &+\beta_7\cdot\mathrm{hispanic}_{i}+\beta_8\cdot\mathrm{nodegree}_{i}\\ &+\beta_9\cdot\mathrm{married}_{i}+\varepsilon_i \end{aligned}$

　推定結果は以下の通りであった。 $\mathrm{RCT}$ であるDehejia-Wahba Sampleの推定結果は $1,676$ $で有意であった。
　他方でCPS1の推定結果は $699$ $で有意でも無かった。これは4.5.1で示したように、そもそも説明変数の分布が大きく相違しており、選択バイアスが発生している。
　CPS3での推定結果は $\mathrm{RCT}$ な結果に近いものの、このデータセットは1976年春の段階で非雇用なサンプルに非介入グループを限定化したもので、ad hocな調整が為されているものである点に注意が必要である。

データセット	推定値	標準誤差	t値	p値
Dehejia-Wahba Sample	$1676$	$639$	$2.62$	$0.00898$
CPS1	$699$	$548$	$1.28$	$0.202$
CPS3	$1548$	$781$	$1.98$	$0.0480$

4.5.3　傾向スコアにおける効果検証

　傾向スコアを用いたマッチングを行った結果、以下のとおりとなった*2。
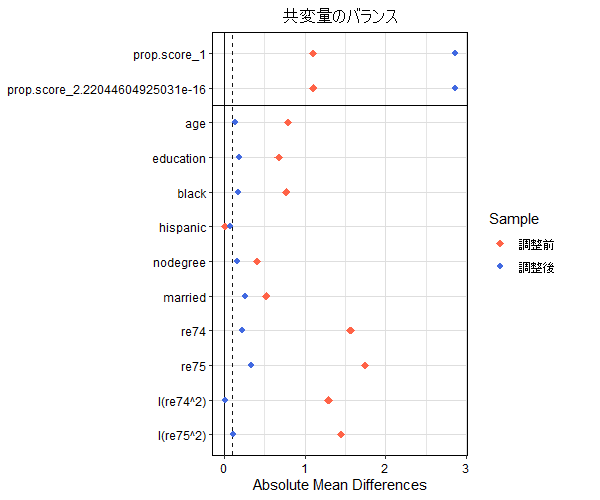
　IPWでは傾向スコアでウェイトが付くため、介入集団と非介入集団との傾向の乖離が非常に大きい場合、一方の標本が異常に大きく影響を与えることになる。このため、そうした傾向が乖離した集団同士での比較ではIPWは信頼しづらい結果をもたらすことが多い。

傾向スコアを用いたマッチング結果(左：傾向スコアマッチング/右：IPW)

　このようにデータセット自体およびその生成過程が分かっていないと、そのモデルの結果がより信頼性の高いものなのかを判断することは非常に困難である。

#####################################
### LaLonde(1986)を用いた効果検証 ###
#####################################

### 各種パッケージの読込
library("tidyverse")
library("haven") # SAS, STATAのデータを読み込むパッケージ
library("broom")
library("MatchIt")
library("WeightIt")
library("cobalt")

library("ggplot2")

### データセットを準備
# 生データを読み込む
cps1_data <- read_dta("https://users.nber.org/~rdehejia/data/cps_controls.dta")
cps3_data <- read_dta("https://users.nber.org/~rdehejia/data/cps_controls3.dta")
nswdw_data <- read_dta("https://users.nber.org/~rdehejia/data/nsw_dw.dta")

# NSWデータから介入標本(treat=1)のみ取り出してCPS1における介入集団として扱う
cps1_nsw_data <- nswdw_data %>% filter(treat == 1) %>% rbind(cps1_data)

# NSWデータから介入標本(treat=1)のみ取り出してCPS3における介入集団として扱う
cps3_nsw_data <- nswdw_data %>% filter(treat == 1) %>% rbind(cps3_data)


### RCTによる効果検証
nsw_cov <- nswdw_data %>%
  lm(data = .,
     formula = formula(re78 ~ treat + re74 + re75 + age + education + black + hispanic + 
                         nodegree + married)) %>%
  tidy() %>%
  filter(term == "treat")

cps1_reg <- cps1_nsw_data %>%
  lm(data = .,
     formula = formula(re78 ~ treat + re74 + re75 + age + education + black + hispanic + 
                         nodegree + married)) %>%
  tidy() %>%
  filter(term == "treat")

cps3_reg <- cps3_nsw_data %>%
  lm(data = .,
     formula = formula(re78 ~ treat + re74 + re75 + age + education + black + hispanic + 
                         nodegree + married)) %>%
  tidy() %>%
  filter(term == "treat")

# 傾向スコアによる効果推定
m_near <- matchit(formula = formula(treat ~ age + education + black + hispanic + nodegree +
                                      married + re74 + re75 + I(re74^2) + I(re75^2)),
                  data = cps1_nsw_data,
                  method = "nearest")

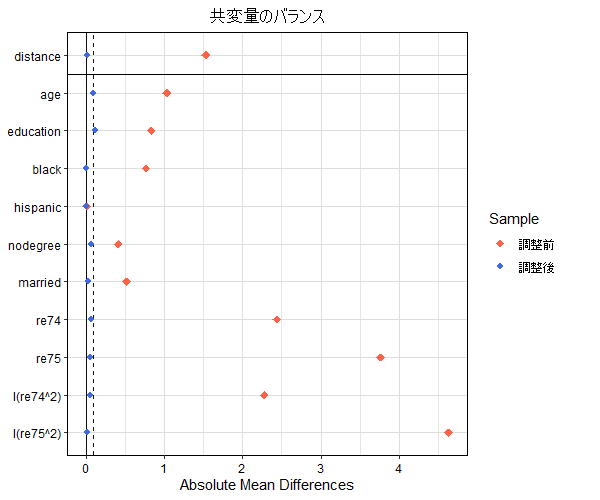
# 共変量のバランスを確認
love.plot(m_near, threshold = 0.1, abs = T, grid = T, 
          shapes = c(18, 20), color = c("tomato", "royalblue"), 
          sample.names = c("調整前", "調整後"),
          title = "共変量のバランス")

# マッチング後のデータを作成
matched_data <- match.data(m_near)

# マッチング後のデータで効果推定
PSM_result_cps1 <- matched_data %>% 
  lm(re78 ~ treat, data = .) %>%
  tidy()

PSM_result_cps1

# IPWによる効果推定
weighting <- weightit(formula = formula(treat ~ age + education + black + hispanic +
                                          nodegree + married + re74 + re75 + I(re74^2) +
                                          I(re75^2)),
                      data = cps1_nsw_data,
                      method = "ps",
                      estimand = "ATE")
love.plot(weighting, threshold = 0.1, abs = T, grid = T, 
          shapes = c(18, 20), color = c("tomato", "royalblue"), 
          sample.names = c("調整前", "調整後"),
          title = "共変量のバランス")

IPW_result <- cps1_nsw_data %>%
  lm(data = .,formula = re78 ~ treat,
     weights = weighting$weights) %>%
  tidy()

IPW_result

今回のまとめ

$\mathrm{LaLonde(1986)}$ のデータを用いて実証分析を行った。

分析方法次第で結果は大きく変化し得る。データセット自体およびその生成過程が分かっていない限り、そのモデルの結果がより信頼性の高いものなのかを判断することは非常に困難である。そのため、そうしたものに興味を払うことが絶対的に必要である。

次回

power-of-awareness.com

*1:最末尾左は「学歴」( $\mathrm{education}$ )変数の分布、右は各ダミー変数の値(テーブル)である。

*2:IPWによるバランスにおいて、2つ目の傾向スコアはなぜこのような値が出ているのか、よく分からなかった。

前回

4. 傾向スコアを用いた分析

4.5 LaLonde(1986)を用いた実証分析

4.5.1 データセット

4.5.2 RCTにおける効果検証

4.5.3 傾向スコアにおける効果検証