「大人の教養・知識・気付き」を伸ばすブログ

一流の大人（ビジネスマン、政治家、リーダー…）として知っておきたい、教養・社会動向を意外なところから取り上げ学ぶことで“気付く力”を伸ばすブログです。データ分析・語学に力点を置いています。　→現在、コンサルタントの雛になるべく、少しずつ勉強中です(※2024年1月21日改訂)。

MENU

効果検証入門（04/08）

経済学 機械学習

　計量経済学の知見をより深めるべく

効果検証入門〜正しい比較のための因果推論／計量経済学の基礎

効果検証入門〜正しい比較のための因果推論／計量経済学の基礎

Amazon

を基に因果推論と計量経済学を学んでいく。

前回

power-of-awareness.com

4.　傾向スコアを用いた分析

　回帰分析では共変量の選定が重要だが、それは同時に難しい過程である。実際の分析では目的変数Yがどのような仕組みで決定されているかについて不充分な情報しか得られない場合がある。また目的変数と説明変数との関係として線形・非線形の決定も同様に難しい。推定される効果も標本の特徴で介入変数の効果が変わり得る場合に推定される効果の性質が異なるという問題がある。
　これから議論する傾向スコアは各標本において介入が行われる確率を表す。傾向スコアを用いた分析は介入が行われた仕組みに注目し、介入グループと非介入グループのデータの性質を似せる操作を行うことで、上記問題点を回避させるような方法である。
　CIAではモデルに利用されている共変量\boldsymbol{X}_iの値が同じ標本の中で介入がY^{(0)}とは独立に割り振られていることを示していた。このとき　共変量\boldsymbol{X}_iの値が同じ標本の間において介入はランダムに割り振られている状態に等しいため、効果を推定可能であった。これに対して傾向スコアは介入が割り振られる確率である。傾向スコアP(X_i)が同一になるような標本の中では介入がY^{(0)}とは独立に割り振られているという仮定に基づいている。したがって共変量から算出した介入の割り振り確率で条件づけた標本の中で介入の割り振りが独立だと考える点が、傾向スコアと回帰分析による推定との差異である。

4.1　傾向スコアの推定

　傾向スコアは大抵の場合、直接観測できない。そこで推定することになるが、機械学習（たとえば勾配ブースティング決定木）を用いる手法も考えられるが、ここではロジスティック回帰の利用を考えることとする。たとえばロジスティック回帰では介入変数Zの値を目的変数とした

\begin{aligned} Z_i&=\displaystyle{\frac{1}{1+\exp\left\{-(\boldsymbol{X}_i\boldsymbol{\beta}+\varepsilon_i)\right\}}},\\ P\{\boldsymbol{X}\}&=\hat{Z}_i=\displaystyle{\frac{1}{1+\exp\left(-\boldsymbol{X}_i\hat{\boldsymbol{\beta}}\right)}} \end{aligned}

で与えられる。ここで\boldsymbol{X}={}^{t}(Y,X_1,\cdots,X_k)は説明変数（Yは介入変数）、\varepsilon_iは誤差項、\boldsymbol{\beta}は推定対象の母数（ベクトル）である。

4.2　傾向スコアを利用した効果推定

　傾向スコアを用いた分析方法として、①得た傾向スコアを利用して標本同士をマッチングさせる傾向スコアマッチング、②傾向スコアを標本の重みとして利用する逆確率重み付き推定を紹介する。

4.2.1　傾向スコアマッチング

　介入が行われているグループからサンプリングし、その標本と近い値の傾向スコアを持つ標本を介入が行われていないグループからマッチングさせてペアにする。その後、ペアの中で算出した目的変数の差の平均を効果の推定値というのが傾向スコアマッチングのアイディアである。
　傾向スコアが同じ値を持つ標本の中であれば介入変数ZはY^{(0)}とは無関係に決定していると考えられるため、この中でグループ間比較をしても選択バイアスの影響を受けないため、このような措置を取る。したがってマッチングでは傾向スコアごとにグループ間を比較し、それらの結果をグループに属している標本の数を重みとした加重平均により効果を推定する。このときマッチングは母集団における以下のような推定値

\begin{aligned} \hat{\tau}_{\mathrm{match}}=E\left[E[Y|P(X),Z=1]-E[Y|P(X),Z=0]|Z=1]\right] \end{aligned}

を算出していることになる。これは介入を受けた標本における介入効果の期待値で\mathrm{ATT}と呼ばれる。

4.2.2　逆確率重み付き推定

　逆確率重み付き推定(\mathrm{IPW})は傾向スコアを標本の重みとして利用し、与えられたデータ全体での介入を受けた場合の結果の期待値（E[Y^{(0)}]）と介入を受けなかった場合の結果の期待値（E[Y^{(1)}]）を推定し、それらの差分を取ることで効果を推定する。すなわち

\begin{aligned} \bar{Y}^{(1)}&=\displaystyle{\frac{\displaystyle{\sum_{i=1}^{n}\frac{Z_iY_i}{\hat{P}(X_i)}}}{\displaystyle{\sum_{i=1}^{n}\frac{Z_i}{\hat{P}(X_i)}}}},\\ \bar{Y}^{(0)}&=\displaystyle{\frac{\displaystyle{\sum_{i=1}^{n}\frac{(1-Z_i)Y_i}{1-\hat{P}(X_i)}}}{\displaystyle{\sum_{i=1}^{n}\frac{1-Z_i}{1-\hat{P}(X_i)}}}},\\ \hat{\tau}_{\mathrm{IPW}}&=\bar{Y}^{(1)}-\bar{Y}^{(0)} \end{aligned}

とする。
　\mathrm{IPW}は選択バイアスが介入グループと非介入グループとで傾向スコアP(X)、すなわち生起確率が異なることに基づいていると考えるのである。データ全体での平均的な効果を推定している。そのため介入の効果が標本によって異なる場合でもそれを考慮した平均的な効果が推定されることになる。

4.2.3　より良い傾向スコア

　傾向スコアは選択バイアスを除外できる万能な道具ではない。
　近年では傾向スコアを利用して重みづけかマッチングを行った後のデータにおいて共変量のバランスが取れているかが重要であるという見解が一般的になってきている。
　共変量のバランスが取れているかを確認するのに共変量の平均が近い値であるかを確認する（4.X.2参照。）。

4.2.4　傾向スコアと回帰分析の比較

　回帰分析と傾向スコアのどちらを使うかは、

  • 目的変数Yに関して充分な情報を持つ場合は回帰分析
  • 目的変数Yに関する情報が少ない場合は傾向スコア

を用いればよい。

　　 　　　　
メリット
デメリット
　　 回帰分析 ・手軽で取り組みやすい

・モデル設定を上手くやれば標準誤差が小さくなる。		 ・目的変数と共変量を入念にモデリングする必要がある。

・モデル設定のミスでバイアスが発生する。
　　 傾向スコア ・目的変数に対するモデリングが不要

・情報がより得やすいZの決定方法に対するヒアリングや調査のみで済む		 ・計算時間が掛かる。
4.2.5　マッチングとIPWの差

　傾向スコアを用いた効果の推定はたいてい、マッチングと\mathrm{IPW}との結果は一致しない。また回帰分析の結果と一致することもまずない。これｈ推定対象が相違することに起因する。
　マッチングで\mathrm{ATT}の推定を行う場合、Z=1となる各標本に対してそれに似ているZ=0の標本をマッチングし、マッチングされなかったものは捨てられる。
　一方で\mathrm{IPW}は傾向スコアの逆数で重みづけしつつ、すべてのデータにおけるY^{(0)},Y^{(1)}の期待値を推定する。これはZの値にかかわらずすべてのデータで仮に\mathrm{RCT}をしていたらどのような結果だったのか、すなわち\mathrm{ATE}を推定する。したがってすべてのデータでの平均的な効果を推計している。
　このように推定対象がそもそも異なるために結果が異なる場合があることに注意する。

4.3　Rスクリプト

########################
### 傾向スコアの推定 ###
########################
### ロジスティック回帰モデルで傾向スコアを推計
# 二項ロジット回帰モデルの推定
ps_model <- glm(data = biased_data,formula = formula(treatment ~ recency + history + channel),family = binomial)
ps_model$fitted.values # 推計した確率：2値データなので0.5を境界として0,1の判断ができる

# 傾向スコアマッチングにより評価
library(MatchIt)

# 傾向スコアを利用したマッチング
m_near <- matchit(formula = formula(treatment ~ recency + history + channel),
                  data = biased_data,
                  method = "nearest",
                  replace = T)
# マッチング後のデータを作成
matched_data <- match.data(m_near)

# マッチング後のデータで効果を推定
PSM_result <- matched_data %>%
  lm(spend ~ treatment, data =.) %>%
  tidy()
PSM_result

# 逆確率重み付き推定により評価
library("WeightIt")

# まずはウェイトの推定
ls_weighting <- weightit(formula = formula(treatment ~ recency + history + channel),
                         data = biased_data, method = "ps", estimand = "ATE")
# 重み付きデータでの効果の推定
IPW_result <- lm(data = biased_data, formula = formula(spend ~ treatment),
                 weights = ls_weighting$weights) %>% 
  tidy()
IPW_result
4.3.1　介入の推定結果
　　
推定方法
項
推定値
標準誤差
t値
p値
　　 \mathrm{PSM} 切片項
0.659
0.171
3.86
1.13\times10^{-4}
　　 　　 介入項
0.869
0.211
4.11
3.95\times10^{-5}
　　 \mathrm{IPW} 切片項
0.676
0.111
6.09
1.14\times10^{-9}
　　 　　 介入項
0.803
0.157
5.11
3.17\times10^{-7}
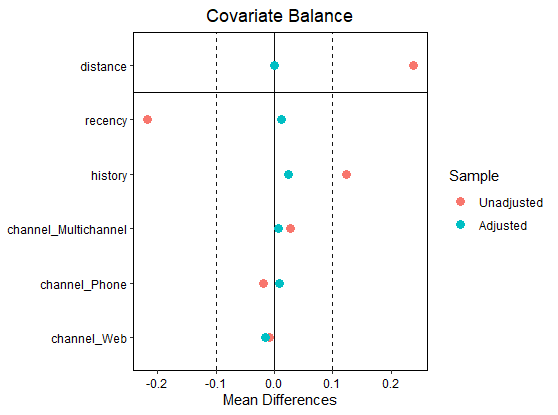
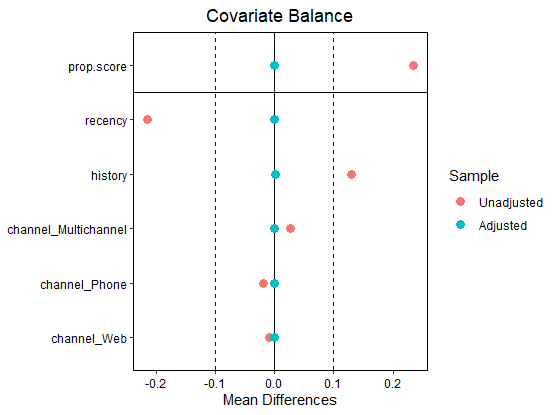
4.3.2　共変量のバランスのグラフ

　横軸は標準化平均差（平均の差をその標準偏差で割ったもの）、縦軸は共変量の種類である。介入の有無で各変数の平均にどの程度差があるかを図示している。調整後の結果がすべて左端（0.0）に並ぶような状況が望ましい。

今回のまとめ

  • 目的変数Yがどのような仕組みで決定されているかについて不充分な情報しか得られない場合、傾向スコアを用いた分析が有用である
  • 傾向スコアは介入が割り振られる確率である
  • 傾向スコアを用いた分析方法として、①得た傾向スコアを利用して標本同士をマッチングさせる傾向スコアマッチング、②傾向スコアを標本の重みとして利用する逆確率重み付き推定などがある
  • 傾向スコアマッチングと逆確率重み付き推定、回帰分析とでは推定対象が相違するから、推定結果が相違する点に注意が必要である

次回

power-of-awareness.com

プライバシーポリシー お問い合わせ