効果検証入門（02/08） - 「大人の教養・知識・気付き」を伸ばすブログ

　計量経済学の知見をより深めるべく

効果検証入門〜正しい比較のための因果推論／計量経済学の基礎

作者:安井翔太
技術評論社

Amazon

を基に因果推論と計量経済学を学んでいく。

前回

power-of-awareness.com

前回
2.　選択バイアスとRCT
今回のまとめ
次回

2.　選択バイアスとRCT

2.3　効果測定の理想的な方法

2.3.3　有意差検定の概要と限界

　介入 $Z$ の効果に対する有意差検定に触れる。メールを配信した場合 $Z_i=1$ における $Y$ の平均 $\bar{Y}^{1}$ と配信しなかった場合 $Z_i=0$ における $Y$ の平均 $\bar{Y}^{0}$ の差が $0$ になるのかを検定する。このような検定では $t$ 検定が頻用される。この検定は標本平均がもともとのデータの分布に拘わらず正規分布で近似できるという中心極限定理を根拠として実施される。有意水準として $0\lt\alpha\lt1$ を所与とする。

(1)	標準誤差の計算	平均の差の標本分散を $\begin{aligned}V=\displaystyle{\frac{\displaystyle{\sum_{i=1}^{n}\left(Y_i^{(0)}-\bar{Y}^{(0)}\right)^2}+\displaystyle{\sum_{j=1}^{m}\left(Y_j^{(1)}-\bar{Y}^{(1)}\right)^2}}{n+m-2}}\end{aligned}$ で推定し、それを元に $\begin{aligned}SE=\sqrt{\displaystyle{\frac{V}{m}+\frac{V}{n}}}\end{aligned}$ で標本誤差を計算する。
(2)	$t$ 値の計算	$t$ 値を $\begin{aligned}t=\displaystyle{\frac{\bar{Y}^{1}-\bar{Y}^{0}}{SE}}\end{aligned}$ で計算する。これはグループ間の平均の差が標準誤差の何単位分かを表す。
(3)	$p$ 値の計算	得られた結果が本当は $0$ であるにもかかわらず計算した $\bar{Y}^{1}-\bar{Y}^{0}$ が得られてしまう確率を表す $p$ 値を $t$ が自由度 $m+n-2$ の $t$ 分布、すなわち $t\sim t(m+n-2)$ に従うことから計算する。
(4)	$p$ 値を有意水準と比較する	$p$ 値が有意水準として事前に与えた $\alpha$ よりも小さければ、平均の差は有意であるとして、本来は $0$ なのに偶然計算した値が得られたわけではないと結論付ける。有意水準よりも大きければ偶然 $0$ からかけ離れた値を得たと結論する。

　または区間推定により推定する場合もある。
　しかし、有意差検定は選択バイアスが大きければ有意を誤って判断しやすくなるなど、使いどころが難しいため、安易に使うことは厳に慎まなければならない。

2.4　実証分析

　Kevin Hillstrom: MineThatData: The MineThatData E-Mail Analytics And Data Mining Challengeのデータを基にここまでの議論を確認する。

データセットにおける変数名

	$\mathrm{recency}$	最後の購入からの経過月数
	$\mathrm{history\_ segment}$	昨年の購入額の階層
	$\mathrm{history}$	昨年の購入額
	$\mathrm{mens}$	昨年に男性物の商品を購入したか
	$\mathrm{womens}$	昨年に女性物の商品を購入したか
	$\mathrm{zipcode}$	郵便番号を基に地区を分類したもの
	$\mathrm{newbie}$	過去12か月以内に新しくユーザになったか
	$\mathrm{channel}$	昨年においてどのチャネルから購入したか
	$\mathrm{segment}$	どのメールが配信されたか
	$\mathrm{visit}$	メールが配信されてから2週間以内にサイトへ来訪したか
	$\mathrm{conversion}$	メールが配信されてから2週間以内に購入したか
	$\mathrm{spend}$	購入した際の購入額

2.4.1　バイアスが特に無いデータを利用した場合

library("tidyverse")

# データの読み込み
email_data <- read.csv(".../Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv",
                       header = T, stringsAsFactors = F)

# 簡単のため男性向けデータのみを考えることとする
unique(email_data$segment) # Womens E-mail, No E-mail, Mens E-mailの3変数でカテゴライズされている様子

# filter()でデータを抽出。mutate()で新しい列を追加
male_df <- email_data %>% 
  filter(segment != "Womens E-Mail") %>% # segmentがWomens E-Mailでないデータを削除
  mutate(treatment = if_else(segment == "Mens E-Mail",1, 0)) # treatment列を介入ありを1,なしを0として挿入

# データを集計する
summary_by_segment <- male_df %>% 
  group_by(treatment) %>%
  summarise(conversion_rate = mean(conversion),
            spend_mean = mean(spend),
            count = n())
summary_by_segment # コンバージョンも売上平均もメール配信者の方が大きそうだ

### 有意差検定を実施
# 男性向けメールが配信されたグループの購買データ
mens_mail <- male_df %>% filter(treatment == 1) %>% pull(spend)

# メールが配信されなかったグループの購買データ
no_mail <- male_df %>% filter(treatment == 0) %>% pull(spend)

# t検定を実施
rct_ttest <- t.test(mens_mail, no_mail, var.equal = T)　# p-value = 1.163e-07なので有意性はありそう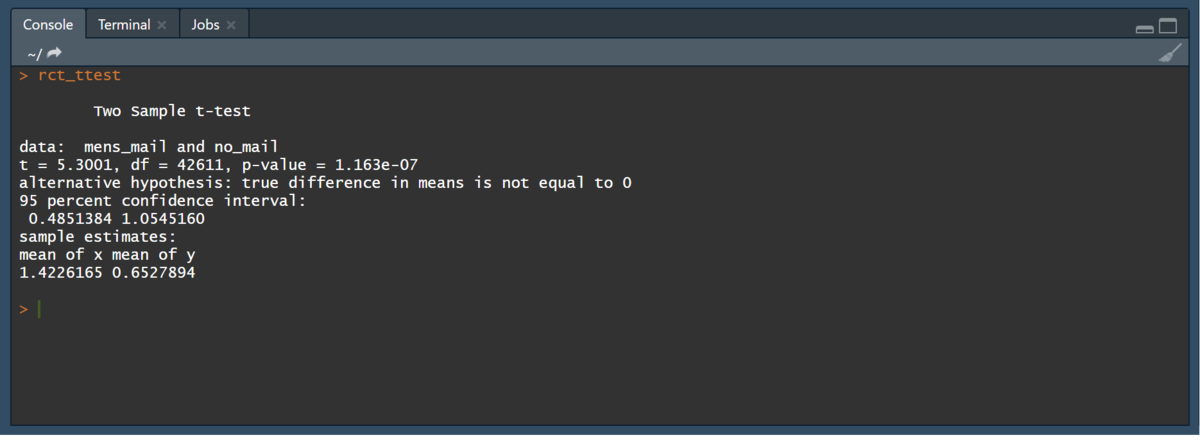

2.4.2　バイアスの有るデータをサンプリングした場合

##########################################
### バイアスのあるデータをサンプリング ###
##########################################

set.seed(1) # 乱数シードを指定：再現性確保のため

### バイアスのあるデータを作成
# サンプル量を半分にする
obs_rate_c <- 0.5
obs_rate_t <- 0.5

# 購買傾向が一定以上あるユーザを重点的にサンプリングしたデータセットを作成する
# (1) メールが配信されていないグループでは金額が一定(300)以下または直近購入時点から6か月未満または
#     接触チャネルが複数(Multichannel)をランダムに半分選んで削除
# (2) メールが配信されているグループでは上記と同じ条件に該当するデータをランダムに半分削除
# -> これにより、潜在的に購入意欲が高いと考えられるユーザに対してメールが多く配信されたデータを作り出す
biased_data <- male_df %>% mutate(obs_rate_c = if_else((history > 300)|(recency < 6)|(channel == "Multichannel"),
                                                       obs_rate_c, 1),
                                  obs_rate_t = if_else((history > 300)|(recency < 6)|(channel == "Multichannel"),
                                                       1, obs_rate_t),
                                  random_number = runif(n = NROW(male_df))
                                  ) %>% filter(
                                    (treatment == 0 & random_number < obs_rate_c)|(treatment = 1 & random_number < obs_rate_t)
                                  )
# 選択バイアスのあるデータで平均を比較
summary_by_segment_biased <- biased_data %>% group_by(treatment) %>% summarise(conversion_rate = mean(conversion),
                                                                               spend_mean = mean(spend),
                                                                               count = n())
summary_by_segment_biased # コンバージョンも売上平均もメール配信者の方が大きそうだ

# t検定を実施
# (1) 男性向けメールを配信した購買データを抽出
mens_mail_biased <- biased_data %>% filter(treatment == 1) %>% pull(spend)
# (2) メールを配信しなかった購買データを抽出
no_mail_biased <- biased_data %>% filter(treatment == 0) %>% pull(spend)

rct_ttest_biased <- t.test(mens_mail_biased,no_mail_biased, var.equal = T)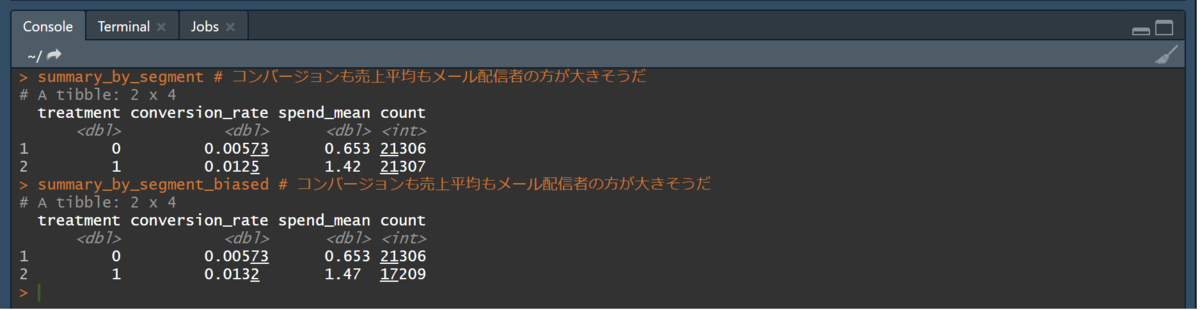

※直上の画像において上(summary_by_segment)がバイアスを持たせていないデータ、下(summary_by_segment_biased)がバイアスの有るデータ

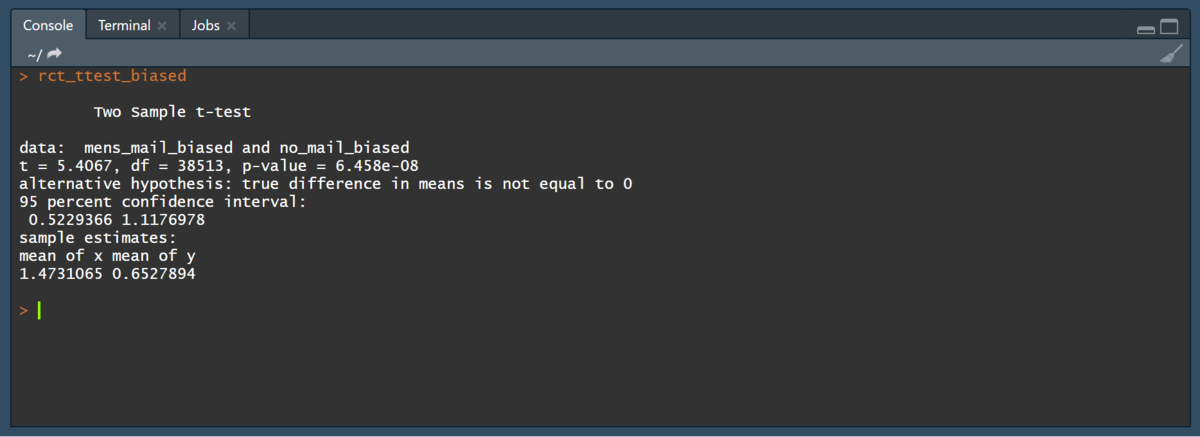
　バイアスデータのコンバージョンや購買額の平均が増大していたこともあり、 $t$ 検定における $p$ 値は先程よりも小さくなっている。

2.5　因果推論の必要性

　 $\mathrm{RCT}$ では効果を検証すべく介入が無作為に割り当てられるような状況を作り出す必要がある。そのため、介入が目的地に与える影響を度外視しており、調査に当たっては多大なコストが掛かる*1。
　理想的には $\mathrm{RCT}$ を活用してデータを設計したいもののそれが不可能であるという中でその結果をなるべく近似するような方法論を提供するのが計量経済学および因果推定論である。ただし選択バイアスを理解して慎重に分析を設計することが前提条件になる。

2.6　選択バイアスが発生する理由

　選択バイアスはたいてい、介入 $Z_i$ の選択を操作できる存在のインセンティブに左右される。このように介入を選択できる人やシステムがインセンティブを高めようと選択した結果として現れるため、誰のどのような意思決定が選択バイアスを生み出すのかをある程度は想定し得る。ただし分析者が認知していない事由は考慮できない。そのため、洞察力を働かせ、その仮説を基に分析を進めることが肝要である。

2.7　バイアスが考慮されたPDCA

　バイアスの有る評価を基にしたPDCAサイクルが生じると、得られた改善の知見は選択バイアスの作り方に過ぎないことが多く、見せかけの改善に留まる場合が多い。この場合、

本当に $\mathrm{KPI}$ を改善しているか不明なものにコストを支払い続ける
蓄積される知見の多くが選択バイアスの作り方になってしまう

という問題を抱えることになる。

今回のまとめ

介入効果の有無は統計的仮説検定で検知し得る。しかし選択バイアスがあればその精度を歪めることになるため、安易な利用は厳に慎むべきである。

$\mathrm{RCT}$ を行うにはコストが高すぎるため、可能な限りその場合の結果を近似する計量経済学および因果推定論の知見を活用することになる。

次回

power-of-awareness.com

*1:ビジネスであれば目的（売上等）を最大化するのが至上命題であるにもかかわらず介入の影響を検知することを最優先にすることで目的が損なわれ得るのでは本末転倒であるということである。

前回

2. 選択バイアスとRCT

2.3 効果測定の理想的な方法

2.3.3 有意差検定の概要と限界

2.4 実証分析

2.4.1 バイアスが特に無いデータを利用した場合

2.4.2 バイアスの有るデータをサンプリングした場合

2.5 因果推論の必要性

2.6 選択バイアスが発生する理由

2.7 バイアスが考慮されたPDCA