効果検証入門（07/08） - 「大人の教養・知識・気付き」を伸ばすブログ

　計量経済学の知見をより深めるべく

効果検証入門〜正しい比較のための因果推論／計量経済学の基礎

作者:安井翔太
技術評論社

Amazon

を基に因果推論と計量経済学を学んでいく。

5.　差分の差分法(DID)とCausalImpact
今回のまとめ
次回

5.　差分の差分法(DID)とCausalImpact

5.1　DID

5.1.1　DIDが必要になる状況

　実際のデータセットには介入・非介入の各グループに同質なサンプルが存在しない場合がよくある。非介入サンプルが存在しない場合、代替となるデータを持ってくることが考えられるものの、それでは選択バイアスを発生させる。
　そこで $\mathrm{DID}$ は介入前後の差分を介入されたグループと介入されなかったグループとでそれぞれ算出し、さらにそれらのグループで差を取るという2つの差分を取ることで選択バイアスを勘案する。

　非介入グループのデータ変化と介入グループが仮に介入を受けなかった場合の変化が一致するという「平行トレンド仮定」を前提とする。
　しかし、平行トレンド仮定を満たすか否かは実際には観測できないため、ある程度の期間のデータを見て妥当か検討することもあり得るが、基本的には分析者がデータを生み出した地域や現象についてどのような解釈をしているかに依存する。
　もしトレンドが同一ではない場合、

仮定を満たさないと考えられるデータを除外する
共変量としてトレンドの乖離を説明するような変数をモデルに加える

という対策が考えられる。しかし

効果の影響を調べたい変数が複数の場所や時期で得られている必要がある
どのデータを使うかが分析者の仮説に依存する

ことが欠点である。

5.2　CausalImpact

　 $\mathrm{CausalImpact}$ は $\mathrm{DID}$ の欠点を補うべく、さまざまな種類の変数 $X$ を利用して目的変数 $Y$ を上手く予想できるようなモデルを介入が行われる前の期間のみで作成する。
　学習されたモデルは $X$ を入力すると介入前の状態の $Y$ を予測するため、介入後の $X$ のデータを入力することで介入が行われなかった場合の $Y$ の値を予測として出力するため、この予測値と観測した $Y$ の差分を取ればよい。
　 $\mathrm{CausalImpact}$ においても有用なデータを見つけることが大きな争点になる。

5.2.1　Rによるテスト

####################
### CausalImpact ###
####################

library("tidyverse")
library("broom")
library("Ecdat")
library("CausalImpact")

# 分析対象から外す州
skip_states <- c(3,9,10,22) # タバコの規制を行なっていた州
skip_states <- c(skip_states,21,23,31,33,48) # タバコに対する税金が1988年以降50セント以上増えた州

# データの読み込み
Cigar <- Cigar %>% 
  filter(!state %in% skip_states,
         year >= 70) %>%
  mutate(area = if_else(state == 5, "CA", "Rest of US"))

# データの準備
Cigar_did_sum <- Cigar %>% 
  mutate(post = if_else(year > 87,1,0),
         ca = if_else(state == 5, 1, 0),
         state = factor(state),
         year_dummy = paste("D", year, sep ="_")) %>%
  group_by(post, year, year_dummy, ca) %>% 
  summarise(sales = sum(sales * pop16)/sum(pop16))

# カリフォルニア州とそれ以外の2集団に対する分析
Cigar_did_sum_reg <- Cigar_did_sum %>%
  lm(data = ., sales ~ ca + post + ca:post + year_dummy)  %>% 
  tidy() %>%
  filter(!str_detect(term, "state"),
         !str_detect(term, "year"))

Cigar_did_sum_logreg <- Cigar_did_sum %>%
  lm(data = ., log(sales) ~ ca + post + ca:post + year_dummy)  %>% 
  tidy() %>%
  filter(!str_detect(term, "state"),
         !str_detect(term, "year"))

print(Cigar_did_sum_reg)
print(Cigar_did_sum_logreg)

###
Y <- Cigar %>% filter(state == 5) %>% pull(sales)

X_sales <- Cigar %>%
  filter(state != 5) %>%
  dplyr::select(.,state, sales, year) %>%
  spread(state, sales) # MASS::selectが読み込まれるのでdplyr::としておくこと!

pre_period <- c(1:nrow(X_sales))[X_sales[,"year"] < 88]
post_period <- c(1:nrow(X_sales))[X_sales[,"year"] >= 88]

CI_data <- cbind(Y,X_sales) %>% dplyr::select(-year)

# CausalImpactによる分析
impact <- CausalImpact::CausalImpact(CI_data,
                                     pre.period = c(min(pre_period), max(pre_period)),
                                     post.period = c(min(post_period), max(post_period))
                                     )
plot(impact)

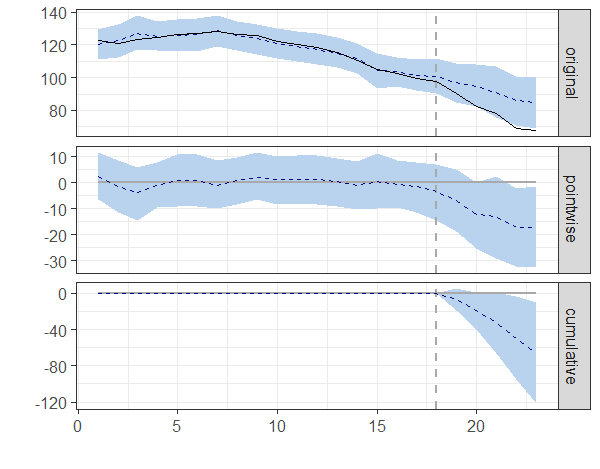5.3　実験補佐

　 $\mathrm{DID}$ や $\mathrm{CausalImpact}$ による分析は実験が限定的にしか行えない環境において重宝される。ただしこれらは効果を分析したい介入がほかの介入や施策と同時に導入される場合、その効果を分析することは出来ない。

今回のまとめ

差分の差分法( $\mathrm{DID}$ )と $\mathrm{CausalImpact}$ は非介入グループのデータ変化と介入グループが仮に介入を受けなかった場合の変化が一致するという「平行トレンド仮定」を前提として介入前後の差分を介入されたグループと介入されなかったグループとでそれぞれ算出し、さらにそれらのグループで差を取るという2つの差分を取ることで選択バイアスを勘案する。

$\mathrm{CausalImpact}$ は $\mathrm{DID}$ の欠点を補うべく、さまざまな種類の変数 $X$ を利用して目的変数 $Y$ を上手く予想できるようなモデルを介入が行われる前の期間のみで作成する。

次回

power-of-awareness.com

5. 差分の差分法(DID)とCausalImpact

5.1 DID

5.1.1 DIDが必要になる状況

5.2 CausalImpact

5.2.1 Rによるテスト

5.3 実験補佐