Rによるデータサイエンス（06/21） - 「大人の教養・知識・気付き」を伸ばすブログ

　Rについて

Rによるデータサイエンス(第2版):データ解析の基礎から最新手法まで

作者:金明哲
森北出版

Amazon

をベースに学んでいく。
　今回は対応分析（PP.85-96）を扱う。

前回
7.　対応分析
- 7.1　対応分析の基本的な考え方
- 7.2　Rのスクリプトと実行結果
補足　スペック情報
次回

前回

power-of-awareness.com

7.　対応分析

　対応分析（コレスポンデンス分析）は1970年代から普及し始めた質的データの解析方法である。類似概念としては数量化Ⅲ類などがある。
　大きな表におけるカテゴリカル変数の関係を要約的に記述することができる。また次元を縮約し少ない次元で度数表における行と列の関係をグラフィカルに表示できる。この手法の利点を引き出すには以下の3つの基準が満たされる必要がある*1：

	(1)	単純な統計解析で構造を発見するのが困難なほどデータ行列が巨大であるか。
	(2)	カテゴリー間の距離計算が意味をもつように変数は同質であるか。
	(3)	構造が未知のデータであるか。

他方で、

	(1)	異なるデータセットに含まれる点の距離は定義できない。
	(2)	効果、もしくは交互作用に対する優位性検定は含まれない。

という欠点がある。

7.1　対応分析の基本的な考え方

　対応分析の基本的な考え方は「分割表において行の項目と劣の項目の相関が最大になるように行・列の双方を並び替え、関連性が強いもの同士が近似になるような値を取るように処理を行う」というものである。

　まず簡単な度数に関する分割表を考える。 $r\times c$ 行列 $F=(f_{ij})_{r\times c}$ で表されるデータ行列について、その各要素を総度数 $n$ で割ったデータを

$\begin{aligned} \{P\}_{r\times c}&=(p_{ij}),\\ p_{ij}&=\displaystyle{\frac{f_{ij}}{n}}, i=1,2,\cdots,r,j=1,2,\cdots,c \end{aligned}$

とおく。

データ行列 $F$ のイメージ

	$x_1$	$x_2$	$\cdots$	$x_j$	$\cdots$	$x_c$	合計
個体 $1$	$f_{11}$	$f_{12}$	$\cdots$	$f_{1j}$	$\cdots$	$f_{1c}$	$f_{1\cdot}$
個体 $2$	$f_{21}$	$f_{22}$	$\cdots$	$f_{2j}$	$\cdots$	$f_{2c}$	$f_{2\cdot}$
$\vdots$	$\vdots$	$\vdots$	$\cdots$	$\vdots$	$\cdots$	$\vdots$	$\vdots$
個体 $i$	$f_{i1}$	$f_{i2}$	$\cdots$	$f_{ij}$	$\cdots$	$f_{ic}$	$f_{i\cdot}$
$\vdots$	$\vdots$	$\vdots$	$\cdots$	$\vdots$	$\cdots$	$\vdots$	$\vdots$
個体 $r$	$f_{r1}$	$f_{r2}$	$\cdots$	$f_{rj}$	$\cdots$	$f_{rc}$	$f_{r\cdot}$
合計	$f_{\cdot1}$	$f_{\cdot2}$	$\cdots$	$f_{\cdot j}$	$\cdots$	$f_{\cdot c}$	$f_{\cdot\cdot}$

　分割表の問題では、通常カイ二乗統計量を用いる。カイ二乗統計量の各セルの値は

$\begin{aligned} \chi_{ij}^2&=\displaystyle{\frac{\left(f_{ij}-\displaystyle{\frac{f_{i\cdot}f_{\cdot j}}{n}}\right)^2}{\displaystyle{\frac{f_{i\cdot}f_{\cdot j}}{n}}}},\\ \chi_{ij}&=\sqrt{n}\displaystyle{\frac{f_{ij}-\displaystyle{\frac{f_{i\cdot}f_{\cdot j}}{n}}}{\sqrt{f_{i\cdot}f_{\cdot j}}}}=\sqrt{n}\displaystyle{\frac{p_{ij}-p_{i\cdot}p_{\cdot j}}{\sqrt{p_{i\cdot}p_{\cdot j}}}} \end{aligned}$

で与えられる。対応分析はデータ行列 $F$ または $P$ を次の式で変換したデータの固有値問題に帰着する。

$\begin{aligned} z_{ij}=\displaystyle{\frac{f_{ij}-\displaystyle{\frac{f_{i\cdot}f_{\cdot j}}{n}}}{\sqrt{f_{i\cdot}f_{\cdot j}}}}=\displaystyle{\frac{p_{ij}-p_{i\cdot}p_{\cdot j}}{\sqrt{p_{i\cdot}p_{\cdot j}}}} \end{aligned}$

　行列 $Z=(z_{ij})_{r\times c}$ を考えたときに分割表の列の効果は $Q=Z^{\prime}Z$ 、行の効果は $P=ZZ^{\prime}$ の固有ベクトル $(U,V)$ をそれぞれ $\displaystyle{\frac{1}{\sqrt{p_{\cdot j}}}},\displaystyle{\frac{1}{\sqrt{p_{i\cdot}}}}$ で規格化した

$\begin{aligned} D_c^{-\frac{1}{2}}U,D_r^{-\frac{1}{2}}L,\ D_c^{-\frac{1}{2}}=\mathrm{diag}(p_{\cdot 1},\cdots,p_{\cdot c}),\ D_r^{-\frac{1}{2}}=\mathrm{diag}(p_{1\cdot},\cdots,p_{r\cdot}) \end{aligned}$

を用いる。 $Q=Z^{\prime}Z$ の固有値が $\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_k,k=\mathrm{rank}(Q)\leq\min\{r,c\}$ である場合、

$\begin{aligned} \chi^2=\displaystyle{\sum_{i=1}^{r}\sum_{j=1}^{c}\displaystyle{\frac{\left(f_{ij}-\displaystyle{\frac{f_{i\cdot}f_{\cdot j}}{n}}\right)^2}{\displaystyle{\frac{f_{i\cdot}f_{\cdot j}}{n}}}}}=n\displaystyle{\sum_{i=1}^{k}\lambda_i} \end{aligned}$

が成り立つ。
　対応分析は分散をカイ二乗統計量＝ $\chi^2$ 距離で計算することでその独自の特徴が現われる。

7.2　Rのスクリプトと実行結果

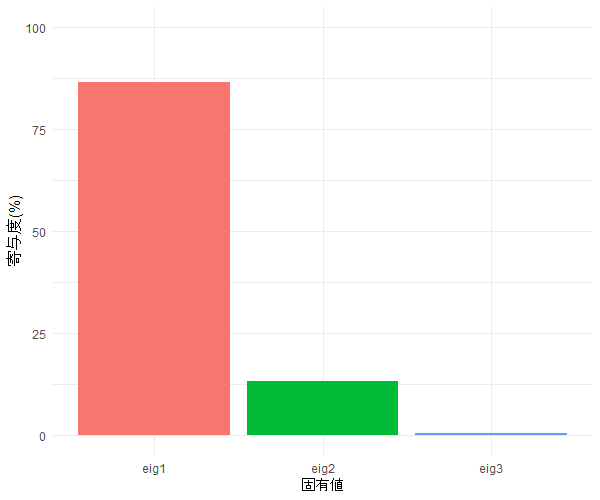
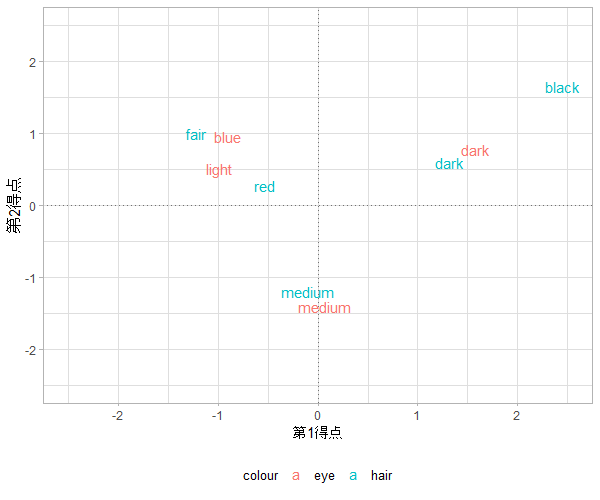
library(MASS)
library(ggplot2)

# データ
data(caith) # 英国居住者の目の色と髪の色に関する集計結果

# データを見てみる
caith

# 対応分析を実施
corres_anl <- corresp(x = caith,nf = min(nrow(caith),ncol(caith)) - 1)
summary(corres_anl)

# 正準相関
caith_eig <- corres_anl$cor^2 # 固有値
round(x = caith_eig,digits = 3)
df_contributions <- data.frame(vars = c("eig1","eig2","eig3"),cnt = round(100 * caith_eig / sum(caith_eig),2))

g <- ggplot(df_contributions,aes(x = vars, y = cnt, fill = vars)) + geom_bar(stat = "identity")
g <- g + theme_minimal() + theme(plot.title = element_text(hjust = 0.5),legend.position = "none",
                                 legend.title=element_text(size = 7),
                                 legend.text=element_text(size = 7))
g <- g + xlab("固有値") + ylab("寄与度(%)")
g <- g + ylim(c(0,100))
plot(g)

# 得点のバイプロット：第1得点、第2得点で殆どを説明できるので、2次元
df_rscore <- corres_anl$rscore
df_cscore <- corres_anl$cscore

df_rscore <- data.frame(names = row.names(df_rscore),
                        colour = rep("eye",nrow(df_rscore)),
                        x = df_rscore[,1],
                        y = df_rscore[,2])
df_cscore <- data.frame(names = row.names(df_cscore),
                        colour = rep("hair",nrow(df_cscore)),
                        x = df_cscore[,1],
                        y = df_cscore[,2])
df_data <- rbind(df_rscore,df_cscore)

# 見やすいように軸
num_max <- max(abs(df_data[,"x"]),abs(df_data[,"y"]))
vc_lim <- c(-round(num_max,1),round(num_max,1))

# 得点のプロット
g2 <- ggplot(df_data,aes(x = x, y = y,label = names, color = colour)) + geom_text()
g2 <- g2 + theme_light() + theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom",
                                 legend.title=element_text(size = 10),
                                 legend.text=element_text(size = 10))
g2 <- g2 + xlab("第1得点") + ylab("第2得点")
g2 <- g2 + xlim(vc_lim) + ylim(vc_lim)
g2 <- g2 + geom_vline(xintercept = 0,linetype = 3,size = 0.5, alpha = 0.7)
g2 <- g2 + geom_hline(yintercept = 0,linetype = 3,size = 0.5, alpha = 0.7)
plot(g2)

caithに適用した結果(左：寄与度、右：第1得点・第2得点のプロット)

補足　スペック情報

エディション	Windows 10 Home
バージョン	20H2
プロセッサ	Intel(R) Core(TM) i5-1035G4 CPU @ 1.10GHz 1.50 GHz
実装 RAM	8.00 GB
システムの種類	64 ビットオペレーティングシステム、x64 ベースプロセッサ
R　バージョン	3.6.3 (2020-02-29)
RStudio　バージョン	1.2.5033

次回

power-of-awareness.com

*1:Sten-Erik Clausen[著]/藤本一男[訳]「対応分析入門原理から応用まで解説◆Rで検算しながら理解する」(オーム社)P.51参照。

前回

7. 対応分析

7.1 対応分析の基本的な考え方

7.2 Rのスクリプトと実行結果

補足 スペック情報

次回

7.　対応分析

7.1　対応分析の基本的な考え方

7.2　Rのスクリプトと実行結果

補足　スペック情報