統計的機械学習の数理100問（14/20） - 「大人の教養・知識・気付き」を伸ばすブログ

　いい加減時代の潮流に乗ろうということで機械学習を学びたいと思う。またRはともかくとしてPythonは未経験であるため、丁度良い書籍として

統計的機械学習の数理100問 with R (with R) (機械学習の数理100問シリーズ)

作者:讓, 鈴木
共立出版

Amazon

統計的機械学習の数理100問 with Python (機械学習の数理100問シリーズ)

作者:讓, 鈴木
共立出版

Amazon

を用いることにする。

前回
5.　正則化
次回

前回

power-of-awareness.com

5.　正則化

標本数 $n$ が変数の数[etx:p]よりも小さい場合、最小二乗法など通常の手段は用いることができない。このときに $\mathrm{Lasso}$ または $\mathrm{Ridge}$ を用いる。

線形回帰において最小化する目的関数に係数の値が大きくならなくするための正則化項を加える。この正則化項を $\mathcal{L}^1$ -ノルムの定数 $\lambda$ 倍にしたものを $\mathrm{Lasso}$ 、 $\mathcal{L}^2$ -ノルムの定数 $\lambda$ 倍にしたものを $\mathrm{Ridge}$ という。

$\mathrm{Lasso}$ では $\lambda$ が大きくなるにつれて係数の推定値が $0$ になる場合が出てきて、 $\lambda\rightarrow\infty$ ではすべての係数の推定値が $0$ になる。このためモデル選択も担う。

　以下、線形回帰を考えるが、一般性を失うことなく切片項 $\beta_0=0$ とし、標本数を $n$ 、変数の数を $p$ として $\boldsymbol{X}\in\mathbb{R}^{n\times p}$ とする。

5.1　Ridge

　行列 ${}^{t}\boldsymbol{X}\boldsymbol{X}$ が特異ではないとも、その行列式が小さい場合、信頼区間が大きくなるなど推定値の信頼性が下がる。そこで定数 $\lambda\geq0$ を用いて

$\begin{aligned} L=\displaystyle{\frac{1}{n}\|\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta}\|^2}+\lambda\|\boldsymbol{\beta}\|_2^2 \end{aligned}$

を最小化することで母数(ベクトル) $\boldsymbol{\beta}$ を推定する*1。これを $\mathrm{Ridge}$ という。
　目的関数 $L$ を $\boldsymbol{\beta}$ で微分すると

$\begin{aligned} \displaystyle{\frac{\partial L}{\partial\boldsymbol{\beta}}}=-\displaystyle{\frac{2}{n}{}^{t}\boldsymbol{X}\left(\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta}\right)+2\lambda\boldsymbol{\beta}} \end{aligned}$

を得るから、 ${}^{t}\boldsymbol{X}\boldsymbol{X}+n\lambda I$ が正則ならば、

$\begin{aligned} &\left(\displaystyle{\frac{2}{n}}{}^{t}\boldsymbol{X}\boldsymbol{X}+2\lambda I\right)\boldsymbol{\beta}=\displaystyle{\frac{2}{n}}{}^{t}\boldsymbol{X}\boldsymbol{Y},\\ \Leftrightarrow&\boldsymbol{\beta}=\left({}^{t}\boldsymbol{X}\boldsymbol{X}+n\lambda I\right)^{-1}\boldsymbol{X}\boldsymbol{Y} \end{aligned}$

が得られる。
　もし $\lambda\gt0$ ならば ${}^{t}\boldsymbol{X}\boldsymbol{X}$ が非負定値であることからその固有値 $p_1,\cdots,p_p$ はすべて非負である。したがって $t\in\mathbb{R}$ に対して

$\begin{aligned} &\mathrm{det}\left({}^{t}\boldsymbol{X}\boldsymbol{X}+n\lambda I-tI\right)=0\\ \Leftrightarrow&t=\mu_1-n\lambda,\cdots,\mu_p+n\lambda\gt0 \end{aligned}$

と、すべての固有値は正である。このため ${}^{t}\boldsymbol{X}\boldsymbol{X}+n\lambda I$ は正則であることが保証される。これは $n,p$ の大小に依存しない。もし $n\lt p$ ならば ${}^{t}\boldsymbol{X}\boldsymbol{X}$ は階数が $n$ 未満で特異である。したがって
　

$\begin{aligned} \lambda\gt\Leftrightarrow {}^{t}\boldsymbol{X}\boldsymbol{X}+n\lambda Iは正則 \end{aligned}$

である。

5.2　劣微分

　 $f(x)=x^2+x+2|x|$ のように絶対値が入ることで微分可能でない点をもつ関数にも微分をできるように概念を拡張できれば、最適化をより柔軟に適用し得る。そこで微分の概念を拡張する。
　前提として $f$ が凸関数であることを仮定する。

劣微分　凸関数 $f:\mathbb{R}\rightarrow\mathbb{R}$ および $x_0\in\mathbb{R}$ が ${}^{\forall}x\in\mathbb{R}$ について

$\begin{aligned} f(x)\geq f(x_0)+z(x-x_0) \end{aligned}$

を満たすような $z\in\mathbb{R}$ の集合を $f$ の $x=x_0$ における劣微分という。

　 $f$ の微分可能な点においては対応する劣微分の値は微分の値と一致する。

5.3　Lasso

　定数 $\lambda\geq0$ を用いて

$\begin{aligned} L=\displaystyle{\frac{1}{2n}\|\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta}\|^2}+\lambda\|\boldsymbol{\beta}\|^2 \end{aligned}$

を最小化することで母数(ベクトル) $\boldsymbol{\beta}$ を推定する方法を $\mathrm{Lasso}$ という。
　 $\mathrm{Lasso}$ の解析には劣微分を用いる。簡単のため、

$\begin{aligned} \displaystyle{\frac{1}{n}\sum_{i=1}^{n}x_{i,j}x_{i,k}}=\begin{cases} 1,&j=k,\\ 0,&j\neq k \end{cases} \end{aligned}$

を仮定し、

$\begin{aligned} s_j:=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}x_{i,j}y_i} \end{aligned}$

とおく。
　このとき $L$ の $\beta_j$ に関する劣微分 *2を求めれば、 $|\beta_j|$ の $\beta_j=0$ での劣微分が $[-1,1]$ であるから、

$\begin{aligned} \displaystyle{\frac{\partial L}{\partial\beta_j }}&=\begin{cases} \displaystyle{-\frac{1}{n}\sum_{i=1}^{n}x_{i,j}\left(y_i-\sum_{k=1}^{p}x_{i,k}\beta_k\right)}+\lambda,&\beta_j\gt0,\\ \displaystyle{-\frac{1}{n}\sum_{i=1}^{n}x_{i,j}\left(y_i-\sum_{k=1}^{p}x_{i,k}\beta_k\right)}-\lambda,&\beta_j\lt0,\\ \displaystyle{-\frac{1}{n}\sum_{i=1}^{n}x_{i,j}\left(y_i-\sum_{k=1}^{p}x_{i,k}\beta_k\right)}+\lambda a,&\beta_j=0,{}^{\forall}a\in[-1,1] \end{cases}\\ &=\begin{cases} \ -s_j+\beta_j+\lambda,&\beta_j\gt0,\\ \ -s_j+\beta_j-\lambda,&\beta_j\lt0,\\ \ -s_j+\beta_j+\lambda a,&\beta_j=0,{}^{\forall}a\in[-1,1] \end{cases} \end{aligned}$

である。したがって

$\begin{aligned} \beta_j=\begin{cases} s_j-\lambda,&s_j\gt\lambda,\\ s_j+\lambda,&s_j\lt-\lambda,\\ 0,&-\lambda\leq s_j\leq\lambda \end{cases} \end{aligned}$

が得られる。
　もし規格化の仮定が満たされない場合は、

において、 $\beta_k,k\neq j$ を固定して $\beta_j$ を更新する。これを $j=1,\cdots,p$ まで何度も繰り返して収束させる。そして各段階で $\beta_j$ を更新する際に $y_i$ をその残差 $r_{i,j}=y_i-\displaystyle{\sum_{k\neq j}x_{i,k}\beta_k}$ で置き換える。また

$\begin{aligned} \begin{cases} \displaystyle{-\frac{1}{n}\sum_{i=1}^{n}x_{i,j}(r_{i,j}-x_{i,j}\beta_j)}+\lambda,&\beta_j\gt0,\\ \displaystyle{-\frac{1}{n}\sum_{i=1}^{n}x_{i,j}(r_{i,j}-x_{i,j}\beta_j)}-\lambda,&\beta_j\lt0,\\ \displaystyle{-\frac{1}{n}\sum_{i=1}^{n}x_{i,j}(r_{i,j}-x_{i,j}\beta_j)}+\lambda a,&\beta_j=0,{}^{\forall}a\in[-1,1] \end{cases} \end{aligned}$

において $s_j=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}r_{i,j}x_{i,j}}$ として、 $\beta_j=S_{\lambda}(s_j)$ を更新する。

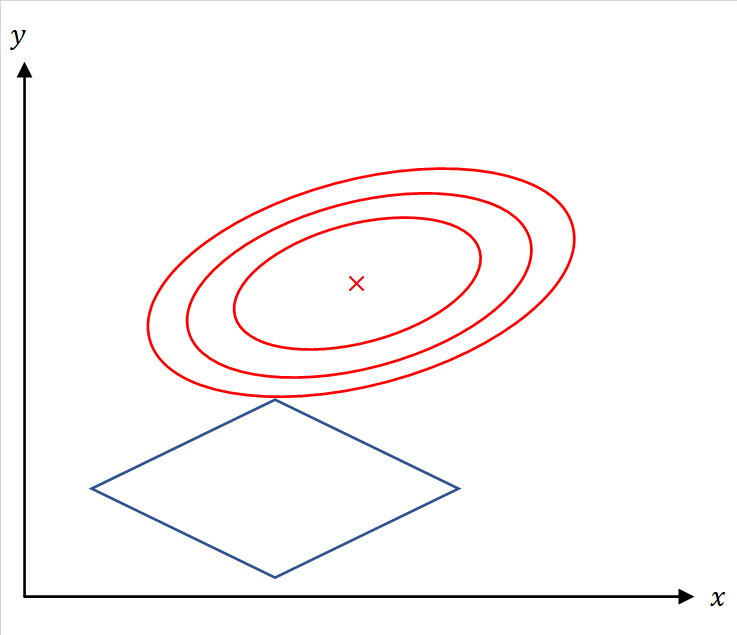
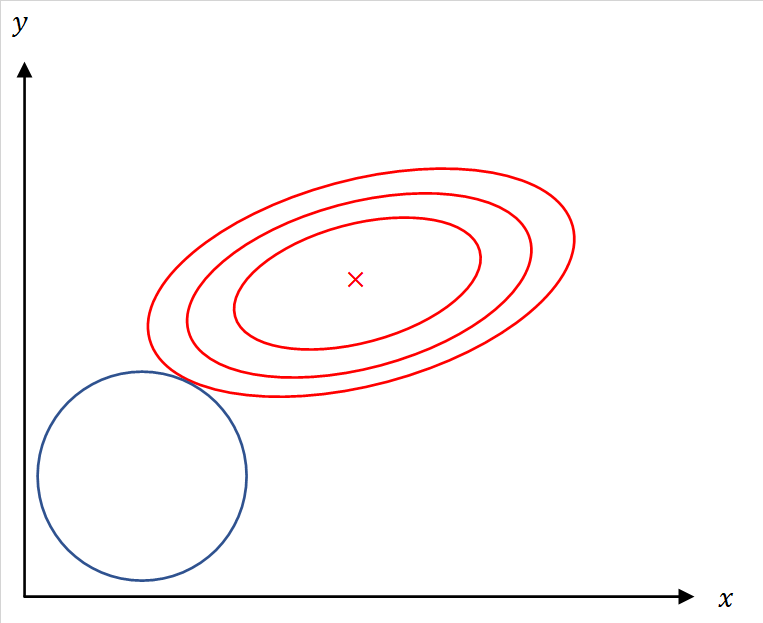
5.4　RidgeとLassoの比較

　 $\mathrm{Ridge}$ および $\mathrm{Lasso}$ はいずれも $\lambda$ が大きくなるにつれて係数の絶対値は減少し $0$ に近づいていく。 $\mathrm{Lasso}$ は $\lambda$ が一定値以上になると係数値が $0$ となり、そのタイミングが変数ごとに相違するために変数選択に用いることができる。このように $\mathrm{Lasso}$ は変数選択に用いることができる。
　簡単のため $p=2$ とすれば、この最適化問題は、中心が $(\hat{\beta}_1,\hat{\beta}_2)$ であるような

$\begin{aligned} \displaystyle{\frac{1}{n}\sum_{i=1}^{n}x_{i,j}x_{i,k}}=\begin{cases} 1,&j=k,\\ 0,&j\neq k \end{cases} \end{aligned}$

の値が等しい点の集合(楕円)と正則化項( $\mathcal{L}^1$ 正則化は $|\beta_1|+|\beta_2|\leq C,$ $\mathcal{L}^2$ 正則化は $\beta_1^2+\beta_2^2\leq C$ )との交点を求める問題に等しい。

LassoおよびRidgeの幾何学的イメージ(左:Lasso/右:Ridge)

5.5　λの設定方法

　 $\lambda$ はクロスバリデーションを適用して決定するのが多い。 $R$ の場合、 $\mathrm{glmnet}$ パッケージを用いると便利である。

###############
### λの設定 ###
###############

library("glmnet")

df <- read.table(file = "C:/Users/Julie/Downloads/crime.txt",header = F,sep = ",")

X <- as.matrix(df[,3:ncol(df)])
y <- df[,1]

cv_fit <- cv.glmnet(X,y) # クロスバリデーションによるλ設定

plot(cv_fit)


lambda_min <- cv_fit$lambda.min

fit <- glmnet(X, y, lambda = lambda_min)
fit$beta

5.6　Rでのシミュレーション

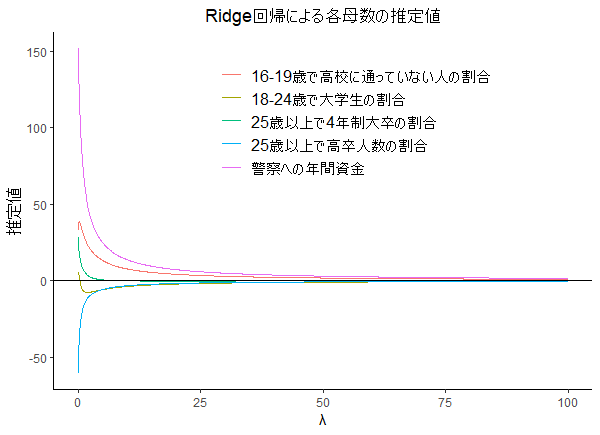
5.6.1　Ridge

#################
### Ridge回帰 ###
#################

library("ggplot2")

# Ridge
ridge <- function(X, y, lambda = 0){
  X <- as.matrix(X)
  X <- scale(X) # 規格化
  
  p <- ncol(X) # 変数の数
  n <- length(y) # 標本数
  
  X_bar <- array(dim = p)
  
  for(i in 1:p){
    X_bar[i] <- mean(X[,i])
    X[,i] <- X[,i] - X_bar[i]
  }
  
  y_bar <- mean(y)
  y <- y - y_bar
  
  beta <- drop(solve(t(X) %*% X + n* lambda * diag(p)) %*% t(X) %*% y)
  beta_0 <- y_bar - sum(X_bar * beta)
  
  return(list(beta = beta, beta_0 = beta_0))
}


# シミュレーション
vc_names <- c("警察への年間資金","25歳以上で高卒人数の割合","16-19歳で高校に通っていない人の割合",
              "18-24歳で大学生の割合","25歳以上で4年制大卒の割合")

df <- read.table(file = "(ファイルパス)",header = F,sep = ",")

X <- df[,3:ncol(df)]
y <- df[,1]

p <- ncol(X)

lambda_seq <- seq(0, 100, 0.1)
coef_seq <- lambda_seq

df_betas <- data.frame(matrix(NA,nrow = p, ncol = length(lambda_seq)))
colnames(df_betas) <- 1:ncol(df_betas)

# Ridge推定
for(lambda in lambda_seq){
  df_betas[,which(lambda_seq==lambda)] <- ridge(X,y,lambda)$beta
}

df_betas_graph <- NULL

for(i in 1:nrow(df_betas)){
  df_betas_graph <- rbind(df_betas_graph,
                          data.frame(lambda = lambda_seq,
                                     var = vc_names[i],
                                     estimate = unlist(df_betas[i,]))
  )
}

# 図示
g <- ggplot(df_betas_graph,aes(x = lambda,y = estimate, group = var, color = var)) + geom_line()
g <- g + xlab("λ") + ylab("推定値")+ labs(title = "Ridge回帰による各母数の推定値",color = "")
g <- g + theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                                 legend.position = c(1, 1),
                                 legend.justification = c(1, 1),
                                 legend.title=element_text(size = 12),
                                 legend.text=element_text(size = 12))
g <- g + geom_hline(yintercept = 0, linetype = 1)
plot(g)

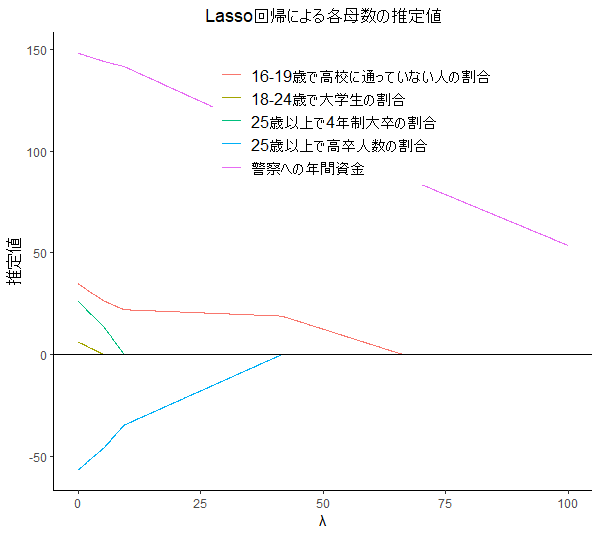
5.6.2　Lasso

#################
### Lasso回帰 ###
#################
soft_th <- function(lambda,x){
  return(sign(x) * pmax(abs(x) - lambda,0))
}

lasso <- function(X, y, lambda = 0){
  X <- as.matrix(X)
  X <- scale(X)
  p <- ncol(X)
  n <- length(y)
  X_bar <- array(dim = p)
  
  for(j in 1:p){
    X_bar[j] <- mean(X[,j])
    X[,j] <- X[,j] - X_bar[j]
  }
  
  y_bar <- mean(y)
  y <- y - y_bar
  eps <- 1
  beta <- array(0, dim = p)
  beta_old <- array(0, dim = p)
  
  while(eps > 0.0001){
    for(j in 1:p){
      r <- y - X[,-j]%*%beta[-j]
      beta[j] <- soft_th(lambda, sum(r * X[,j])/n)
    }
    
    eps <- max(abs(beta - beta_old))
    beta_old <- beta
  }
  beta_0 <- y_bar - sum(X_bar * beta)
  return(list(beta = beta, beta_0 = beta_0))
}

###
vc_names <- c("警察への年間資金","25歳以上で高卒人数の割合","16-19歳で高校に通っていない人の割合",
              "18-24歳で大学生の割合","25歳以上で4年制大卒の割合")

df <- read.table(file = "(ファイルパス)",header = F,sep = ",")

X <- df[,3:ncol(df)]
y <- df[,1]

p <- ncol(X)

lambda_seq <- seq(0, 100, 0.1)
coef_seq <- lambda_seq

df_betas <- data.frame(matrix(NA,nrow = p, ncol = length(lambda_seq)))
colnames(df_betas) <- 1:ncol(df_betas)

# Lasso推定
for(lambda in lambda_seq){
  df_betas[,which(lambda_seq==lambda)] <- lasso(X,y,lambda)$beta
}

df_betas_graph <- NULL

for(i in 1:nrow(df_betas)){
  df_betas_graph <- rbind(df_betas_graph,
                          data.frame(lambda = lambda_seq,
                                     var = vc_names[i],
                                     estimate = unlist(df_betas[i,]))
  )
}

# 図示
g <- ggplot(df_betas_graph,aes(x = lambda,y = estimate, group = var, color = var)) + geom_line()
g <- g + xlab("λ") + ylab("推定値")+ labs(title = "Lasso回帰による各母数の推定値",color = "")
g <- g + theme_classic() + theme(plot.title = element_text(hjust = 0.5),
                                 legend.position = c(1, 1),
                                 legend.justification = c(1, 1),
                                 legend.title=element_text(size = 12),
                                 legend.text=element_text(size = 12))
g <- g + geom_hline(yintercept = 0, linetype = 1)
plot(g)

5.7　Pythonによるシミュレーション

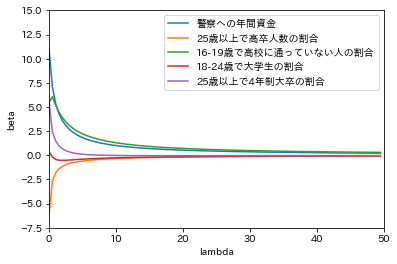
5.7.1　Ridge

import numpy as np
import copy
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib

def ridge(x,y, lam = 0):
    X = copy.copy(x)
    n, p = X.shape
    X_bar = np.zeros(p)
    s = np.zeros(p)
    for j in range(p):
        X_bar[j] = np.mean(X[:,j])
    for j in range(p):
        s[j] = np.std(X[:,j])
        X[:,j] = (X[:, j] - X_bar[j])/s[j]
    y_bar = np.mean(y)
    y = y - y_bar
    
    beta = np.linalg.inv(X.T@X + n * lam * np.eye(p))@X.T@y
    
    for j in range(p):
        beta[j] = beta[j] / s[j]
    beta_0 = y_bar - X_bar.T@beta
    return {'beta': beta, 'beta_0': beta_0}

# テストデータ
df = np.loadtxt("C:/Users/Julie/Downloads/crime.txt", delimiter = ",")
X = df[:,[i for i in range(2,7)]]
p = X.shape[1]
y = df[:,0]
lambda_seq = np.arange(0,50,0.5)
plt.xlim(0,50)
plt.ylim(-7.5,15)
plt.xlabel("lambda")
plt.ylabel("beta")
labels = ["警察への年間資金","25歳以上で高卒人数の割合","16-19歳で高校に通っていない人の割合",
          "18-24歳で大学生の割合","25歳以上で4年制大卒の割合"]

for j in range(p):
    coef_seq = []
    for l in lambda_seq:
        coef_seq.append(ridge(X,y,l)['beta'][j])
    plt.plot(lambda_seq, coef_seq, label = "{}".format(labels[j]))
plt.legend(loc = "upper right")

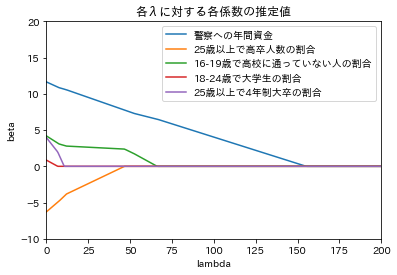
5.7.2　Lasso

#############
### Lasso ###
#############
import numpy as np
import copy

def soft_th(lam, x):
    return np.sign(x) * np.maximum(np.abs(x) - lam, 0)

def lasso(x,y,lam = 0):
    X = copy.copy(x)
    n, p = X.shape
    X_bar = np.zeros(p)
    s = np.zeros(p)
    
    for j in range(p):
        X_bar[j] = np.mean(X[:,j])
    for j in range(p):
        s[j] = np.std(X[:,j])
        X[:,j] = (X[:,j]-X_bar[j])/s[j]
    y_bar = np.mean(y)
    y = y - y_bar
    eps = 1
    
    beta = np.zeros(p)
    beta_old = np.zeros(p)
    
    while eps > 0.0001:
        for j in range(p):
            idx = list(set(range(p)) - {j})
            r = y - X[:,idx]@beta[idx]
            beta[j] = soft_th(lam,r.T@X[:,j]/n)
        eps = np.max(np.abs(beta - beta_old))
        beta_old = beta
    for j in range(p):
        beta[j] = beta[j]/s[j]
    beta_0 = y_bar - X_bar.T@beta
    return {'beta':beta, 'beta_0':beta_0}

# テストデータ
df = np.loadtxt("C:/Users/Julie/Downloads/crime.txt", delimiter = ",")
X = df[:,[i for i in range(2,7,1)]]
p = X.shape[1]
y = df[:,0]
lasso(X,y,20)

lambda_seq = np.arange(0,200,0.5)
plt.xlim(0,200)
plt.ylim(-10,20)
plt.xlabel("lambda")
plt.ylabel("beta")
labels = ["警察への年間資金","25歳以上で高卒人数の割合","16-19歳で高校に通っていない人の割合",
          "18-24歳で大学生の割合","25歳以上で4年制大卒の割合"]

for j in range(p):
    coef_seq = []
    for l in lambda_seq:
        coef_seq.append(lasso(X,y,l)['beta'][j])
    plt.plot(lambda_seq, coef_seq, label = "{}".format(labels[j]))
plt.legend(loc = "upper right")
plt.title("各λに対する各係数の推定値")

#####
from sklearn.linear_model import Lasso
from sklearn.linear_model import LassoCV

Las = Lasso(alpha = 20)
Las.fit(X,y)
Las.coef_

# alphasに指定した値をグリッドサーチする
Lcv = LassoCV(alphas = np.arange(0.1, 30, 0.1), cv = 10)
Lcv.fit(X,y)
Lcv.alpha_
Lcv.coef_

次回

power-of-awareness.com

*1: $\boldsymbol{x}=(x_1,\cdots,x_n)$ に対して、 $\mathcal{L}^1$ -ノルム $\|\boldsymbol{x}\|$ および $\mathcal{L}^2$ -ノルム $\|\boldsymbol{x}\|_2$ は $\|\boldsymbol{x}\|=\sqrt{\displaystyle{\sum_{i=1}^{n}|x_i|}},$ $\|\boldsymbol{x}\|_2=\sqrt{\displaystyle{\sum_{i=1}^{n}x_i^2}}$ で定義される。

*2:記号としては普通の微分と同じ書き方をする。

前回

5. 正則化

5.1 Ridge

5.2 劣微分

5.3 Lasso

5.4 RidgeとLassoの比較

5.5 λの設定方法

5.6 Rでのシミュレーション

5.6.1 Ridge

5.6.2 Lasso

5.7 Pythonによるシミュレーション

5.7.1 Ridge

5.7.2 Lasso

次回