今回やりたいこと
確率試行のシミュレーションをJuliaで扱ってみる。
を参照する。
1. Juliaでの確率分布の扱い
各種の確率分布が持つ性質を理解するには主に3つの方法がある:
- 確率分布から変数をサンプリングする。
- 確率分布の形状をグラフにする。
- 確率分布の統計量を計算する。
Juliaで確率分布を取り扱うにはを用いるのが一般的である。
1.1 Bernoulli分布
using Distributions using PyPlot # グラフの諸設定を行う関数 function set_options(ax, xlabel, ylabel, title; grid = true, gridy = false, legend = false) ax.set_xlabel(xlabel) ax.set_ylabel(ylabel) ax.set_title(title) if grid if gridy ax.grid(axis = "y") else ax.grid() end end legend && ax.legend() end ####################################### ### Bernoulli分布をシミュレートする ### ####################################### d = Bernoulli(0.3) # 分布を作成 # ここからサンプリングする x = rand(d) println(x) # Bernoulli分布からの標本はBool型で与えられる println(Int(x)) # Bool型を整数型に変換する X = rand(d, 1000) X' # 確率を試算 println("******************************") println(pdf(d,1)) println(pdf(d,0)) println(pdf(d,-1)) println("******************************") # 確率質量関数を作成 fig, ax = subplots() ax.bar([0,1], pdf.(d, [0,1])) set_options(ax,"x", "Probs", "Bernoulli Distribution",gridy = true)

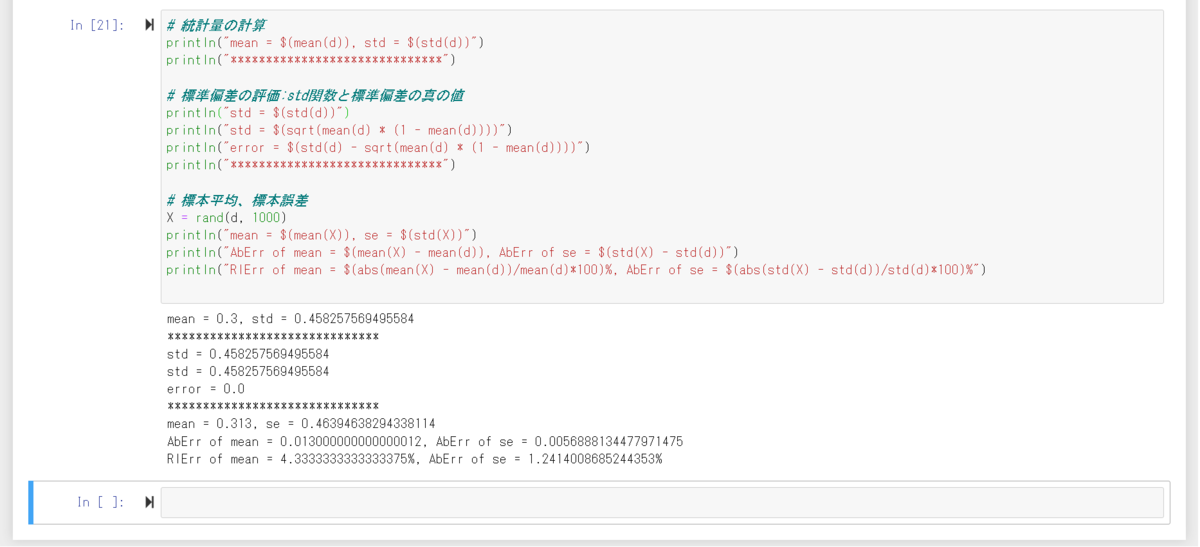
# 統計量の計算 println("mean = $(mean(d)), std = $(std(d))") println("******************************") # 標準偏差の評価:std関数と標準偏差の真の値 println("std = $(std(d))") println("std = $(sqrt(mean(d) * (1 - mean(d))))") println("error = $(std(d) - sqrt(mean(d) * (1 - mean(d))))") println("******************************") # 標本平均、標本誤差 X = rand(d, 1000) println("mean = $(mean(X)), se = $(std(X))") println("AbErr of mean = $(mean(X) - mean(d)), AbErr of se = $(std(X) - std(d))") println("RlErr of mean = $(abs(mean(X) - mean(d))/mean(d)*100)%, AbErr of se = $(abs(std(X) - std(d))/std(d)*100)%")
1.2 二項分布
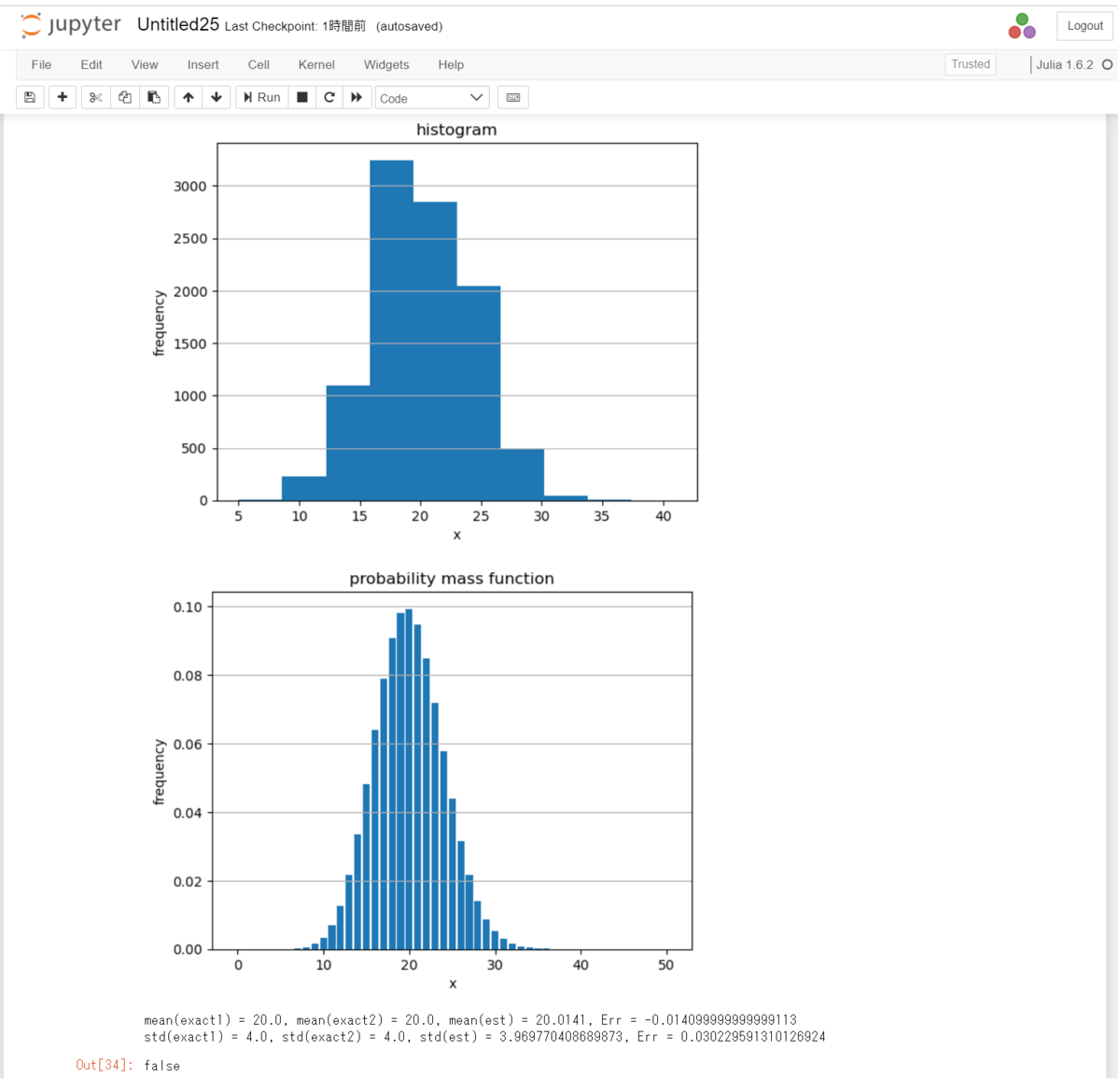
################################## ### 二項分布をシミュレートする ### ################################## n = 100 p = 0.2 # 分布の設定 d = Binomial(n, p) X = rand(d, 10000) fig, ax = subplots() ax.hist(X) set_options(ax,"x", "frequency", "histogram",gridy = true) # 統計量の計算 println("mean(exact1) = $(mean(d)), mean(exact2) = $(n * p), mean(est) = $(mean(X)), Err = $(mean(d) - mean(X))") println("std(exact1) = $(std(d)), std(exact2) = $(sqrt(n * p * (1 - p))), std(est) = $(std(X)), Err = $(std(d) - std(X))") # 確率質量関数 xs = range(0, 50, length = 51) fig, ax = subplots() ax.bar(xs, pdf.(d, xs)) set_options(ax, "x", "frequency", "probability mass function", gridy = true)
1.3 多項分布
# 多項分布をシミュレートする M = 10 d = Multinomial(M, [0.5, 0.3, 0.2]) X = rand(d, 1000) println(X) mean(X, dims = 2) mean(d) cov(X, dims = 2) cov(d) abs.(cov(X, dims = 2) - cov(d)) # 確率質量関数 xs = 0:M fig, ax = subplots() cs = ax.imshow([pdf(d, [x1, x2, M - (x1 + x2)]) for x1 in xs, x2 in xs]', origin = "lower") fig.colorbar(cs) ax.set_xlabel("x1"), ax_set_ylabel("x2") set_options(ax, "x1", "x2", "", grid = false)

