Juliaを使ってみる(05/22)：確率試行のシミュレーション

今回やりたいこと

　確率試行のシミュレーションをJuliaで扱ってみる。

Juliaで作って学ぶベイズ統計学 (KS情報科学専門書)

を参照する。

前回

power-of-awareness.com

1.　確率的試行のシミュレーション

1.1　Bernoulli乱数

　まずは簡単なBernoulli乱数を発生させてみる。

using Distributions

# 母数が0.5のBernoulli分布を導入
bern = Bernoulli(0.5)

# Bernoulli乱数を10個生成
X = rand(bern, 10)
print(X)

# 母数を0.9にしてみる
bern = Bernoulli(0.9)

X = rand(bern, 10)
print(X)

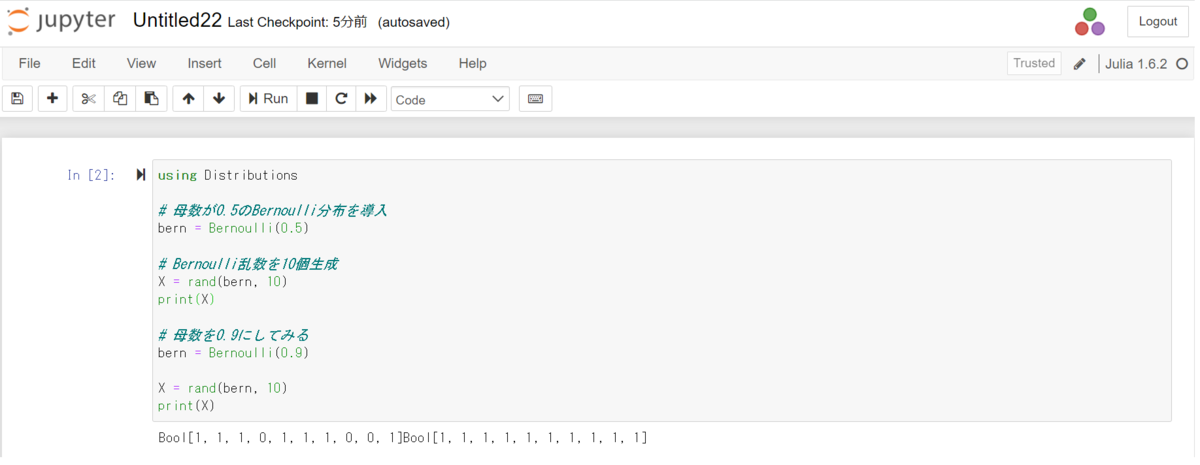
1.2　くじ引きのモデル化

using Distributions

##################################
### くじ引きをモデル化してみる ###
##################################

### 赤玉および青玉の入っている袋AまたはBから玉を取り出す試行をモデル化する

# 母数が0.9のBernoulli分布を導入
bern = Bernoulli(0.9)

# 関数を定義
bag(x::Bool) = x == 1 ? "A" : "B"    # 関数：引数xが1ならば"A"をそうでなければ"B"を返す
ball(y::Bool) = y == 1 ? "赤" : "青" # 関数：引数yが1ならば"赤"をそうでなければ"青"を返す

X = bag.(rand(bern, 30))

# 袋の中から赤玉または青玉を抜き出す試行
function sample()
    # 一方を引く確率は1/2
    x = bag(rand(Bernoulli(1//2))) # // はRational型を表す演算子
    
    # 袋がAならば赤玉が出る確率は1/5
    # 袋がBならば赤玉が出る確率は3/5
    mu = x == "A" ? 1//5 : 3//5      # 関数:袋が"A"ならば赤玉が出る確率として1/5, "B"ならば赤玉が出る確率は3/5
    
    # 玉の抽出
    y = ball(rand(Bernoulli(mu)))
    
    x, mu, y
end

for _ in 1:30
    x, mu, y = sample()
    println("袋: $(x), 玉: $(y)")
end

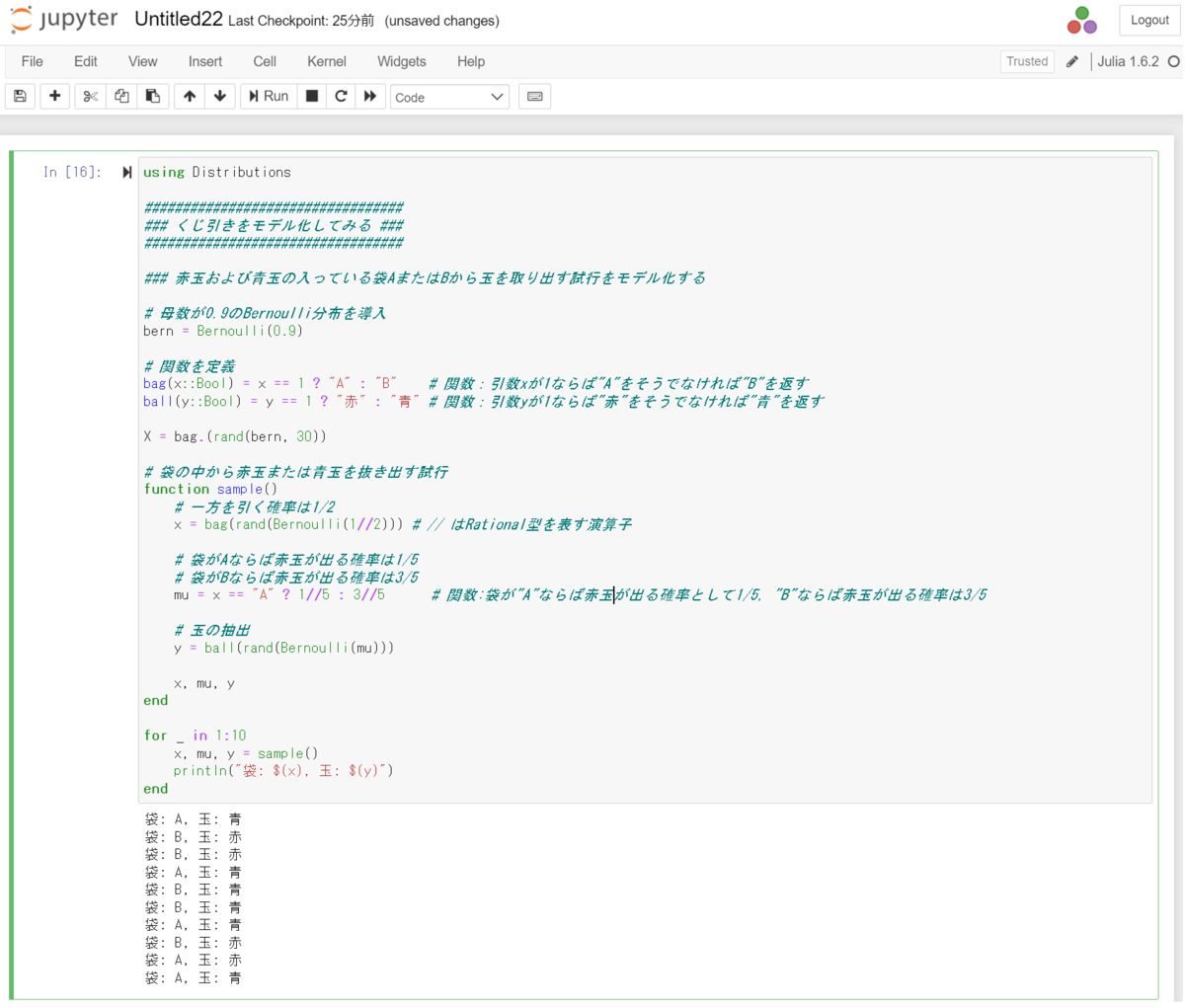
1.3　周辺確率のシミュレーション

　袋から取った玉が赤玉である確率は

である。また袋の選択は五分五分、すなわち

である。は、理論的には

である。
　シミュレーション上は全試行数のうち発生させた試行結果のうちなものの割合を計算すればよい。

##########################
### 周辺確率を計算する ###
##########################

# P(y = "赤")を計算する
maxiter = 1000000
result = []

for _ in 1:maxiter
    x, mu, y = sample()
    push!(result, y)
end

mean(result .== "赤")
# 0.399749

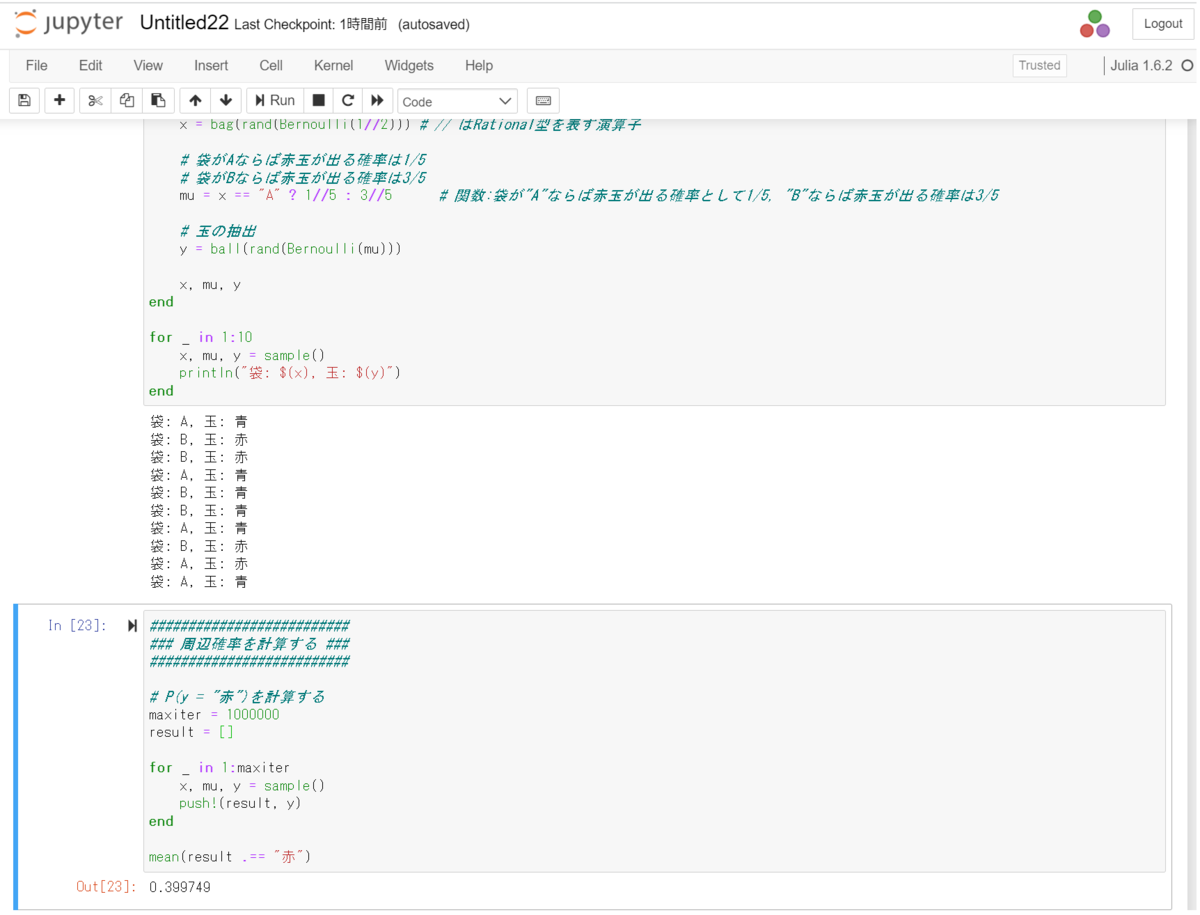
1.4　ポイント

• コンピュータによる繰り返しのシミュレーションによって確率計算が近似的に可能である。
• 計算量を増やす程計算結果として得られる確率は理論的な厳密値に近づいていく。
• 高次元の問題ほど計算が難しく計算量を増やさないとなかなか正解に近づかない。
• 与えられた統計モデルの構造・性質に適した計算手法が作れれば近似精度の向上や計算量の低減が期待できる。

次回

power-of-awareness.com