今回やりたいこと
最適化をJuliaで扱ってみる。
を参照する。
1. 大域最適化と局所最適化
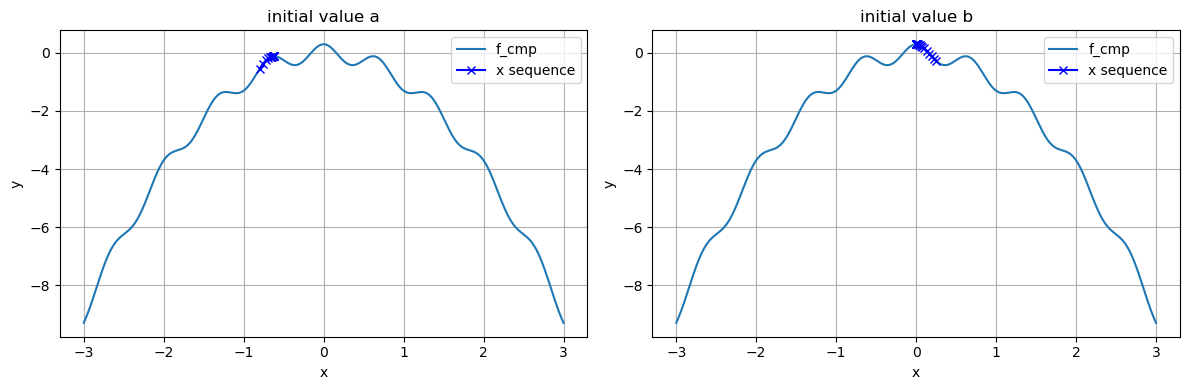
局所最適化に陥っていないかをチェックするため、普通さまざまな初期値を用いて適当な推定値を検討する(機械学習ではこれをハイパーパラメータチューニングという。)。
######################## ### 局所最適解の検討 ### ######################## f_cmp(x) = 0.3*cos(3pi*x) -x^2 # 最適化に向けたパラメータ設定 maxiter = 500 eta = 0.01 # 初期値a x_init_a = -0.8 x_seq_a = gradient_method_1dim(f_cmp, x_init_a, eta, maxiter) f_seq_a = f_cmp.(x_seq_a) # 初期値b x_init_b = 0.25 x_seq_b = gradient_method_1dim(f_cmp, x_init_b, eta, maxiter) f_seq_b = f_cmp.(x_seq_b) # 目的関数の値をステップごとにプロット fig,axes = subplots(2, 1, figsize = (8,4)) axes[1].plot(f_seq_a) axes[1].set_xlabel("iteration"), axes[1].set_ylabel("f") axes[1].set_title("f") axes[2].grid() axes[2].plot(f_seq_b) axes[2].set_xlabel("iteration"), axes[2].set_ylabel("f") axes[2].set_title("f") axes[2].grid() tight_layout() # 関数を可視化する範囲 xs = range(-3, 3, length = 500) # 最適化の過程 fig, axes = subplots(1, 2, figsize = (12,4)) axes[1].plot(xs, f_cmp.(xs), label = "f_cmp") axes[1].plot(x_seq_a, f_cmp.(x_seq_a),color = "b", marker = "x", label = "x sequence") axes[1].set_xlabel("x"), axes[1].set_ylabel("y") axes[1].grid() axes[1].set_title("initial value a") axes[1].legend() axes[2].plot(xs, f_cmp.(xs), label = "f_cmp") axes[2].plot(x_seq_b, f_cmp.(x_seq_b),color = "b", marker = "x", label = "x sequence") axes[2].set_xlabel("x"), axes[2].set_ylabel("y") axes[2].grid() axes[2].set_title("initial value b") axes[2].legend() tight_layout()
2. 最適化によるカーブ・フィッティング
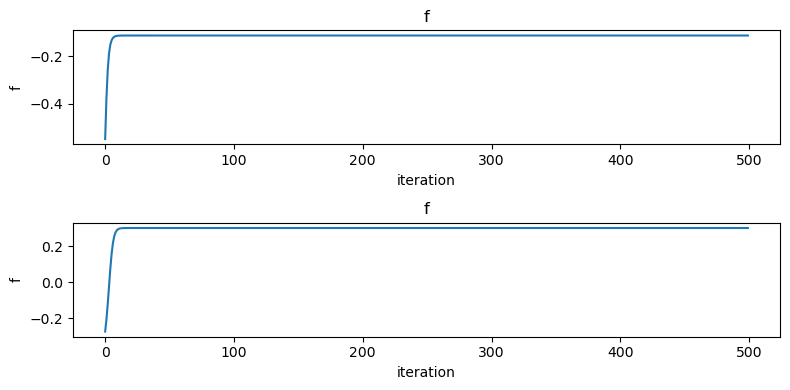
# 適当な切片、係数パラメータを設定 w = [12.0, 10.0] # 予測に用いる関数 f(x) = w[1]*x + w[2] # 関数を可視化する範囲 xs = range(0, 5, length = 100) # データと予測関数の可視化 fig,ax = subplots() ax.plot(xs, f.(xs), label = "function") ax.scatter(X_obs, Y_obs, label = "data") ax.set_xlabel("X"), ax.set_ylabel("Y") ax.grid() ax.legend() # 誤差関数の定義 E(w) = sum([(Y_obs[n] - (w[1] * X_obs[n] + w[2]))^2 for n in 1:length(X_obs)]) # 最適化するパラメータの初期値 w_init = [0.0, 0.0] # 最適化計算の回数 maxiter = 500 # 学習率 eta = 0.01 # 最適化の実行: 最大化アルゴリズムであるから-E[w]を目的関数とする F(w) = -E(w) w_seq = gradient_method(F, w_init, eta, maxiter) f_seq = [F(w_seq[:,i]) for i in 1:maxiter] w1, w2 = w_seq[:,end] println("w_1 = $(w1), w_2 = $(w2)") fig,ax = subplots(figsize = (8,4)) ax.plot(f_seq) ax.set_xlabel("iteration"), ax.set_ylabel("f") ax.grid() # 予測に用いる1次関数 f(x) = w1 * x + w2 # 関数を可視化する範囲 xs = range(0, 5, length = 100) # データと予測関数のプロット fig,ax = subplots() ax.plot(xs, f.(xs), label = "f(x)") ax.scatter(X_obs, Y_obs, label = "data") ax.set_xlabel("x"), ax.set_ylabel("y") ax.grid() ax.legend() ######################################## ### 参考に解析的に計算した結果と比較 ### ######################################## function linear_fit(Y,X) N = length(Y) w1 = sum((Y.-mean(Y)).*X) / sum((X .- mean(X)).*X) w2 = mean(Y) -w1 * mean(X) w1, w2 end w1, w2 = linear_fit(Y_obs, X_obs) println("w_1 = $(w1), w_2 = $(w2)") println("w_1 = $(w_seq[1,end]), w_2 = $(w_seq[2,end])")
2. 数値積分
2.1. 1次元の場合
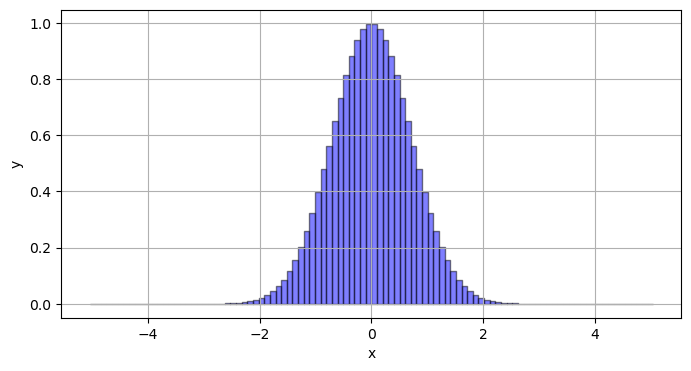
################ ### 積分計算 ### ################ # Gauss積分を数値計算する function approx_integration(x_range, f) Delta = x_range[2] - x_range[1] sum([f(x) * Delta for x in x_range]), Delta end # 近似対象:厳密解はsqrt(pi) f(x) = exp(- x^2) # 等間隔の配列を用意 x_range = range(-5, 5, length = 100) approx, Delta = approx_integration(x_range, f) # 近似値(approx)と厳密解(exact)の比較 println("approx = $(approx)") println("exact = $(sqrt(pi))") # 関数と近似結果の可視化 fig, ax = subplots(figsize = (8, 4)) xs = range(-5, -5, length = 1000) ax.plot(xs, f.(xs), "r-") for x in x_range ax.fill_between([x - Delta * 0.5, x + Delta * 0.5], [f(x), f(x)], [0, 0], facecolor = "b", edgecolor = "k", alpha = 0.5) end ax.set_xlabel("x"), ax.set_ylabel("y") ax.grid()
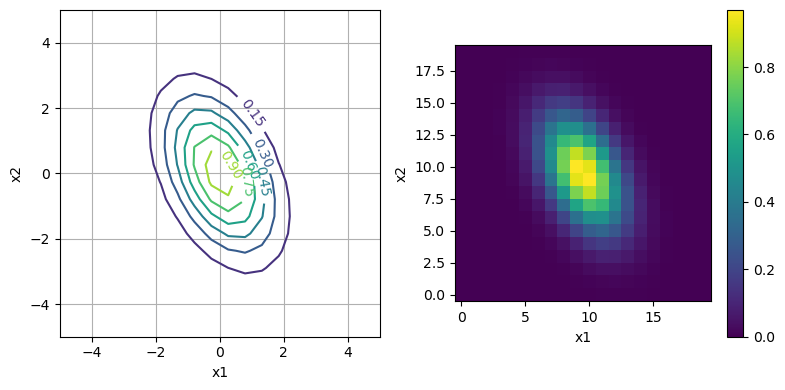
2.2. 多次元の場合
############################ ### 多変数関数の数値積分 ### ############################ D = 2 # ベクトルの成分数 A = [0.5 0.3 0.3 1.0] f2(x) = exp(-0.5 * x' * A * x) # 20x20の区画に分割 L = 20 xs1 = range(-5, 5, length = L) xs2 = range(-5, 5, length = L) fig,axes = subplots(1, 2, figsize = (8, 4)) # 等高線図で可視化 cs = axes[1].contour(repeat(xs1, 1, L), repeat(xs2', L ,1), [f2([x1, x2]) for x1 in xs1, x2 in xs2]') axes[1].clabel(cs) axes[1].grid() axes[1].set_xlabel("x1"), axes[1].set_ylabel("x2") # 色表示 cs = axes[2].imshow([f2([x1, x2]) for x1 in xs1, x2 in xs2], origin = "lower") fig.colorbar(cs) axes[2].set_xlabel("x1"), axes[2].set_ylabel("x2") tight_layout() # 厳密解と比較 # det 関数を用いるべく using LinearAlgebra function approx_integration_2dim(x_range, f) Delta = x_range[2] - x_range[1] sum([f([x1, x2]) * Delta^2 for x1 in x_range, x2 in x_range]), Delta end L = 1000 x_range = range(-5, 5, length = L) approx, Delta = approx_integration_2dim(x_range, f2) println("approx = $(approx)") println("exact = $(sqrt((2pi)^D/det(A)))")