いい加減時代の潮流に乗ろうということで機械学習を学びたいと思う。またRはともかくとしてPythonは未経験であるため、丁度良い書籍として
を用いることにする。
1. 線形回帰
1.7. 決定係数と共線性の検出
以降、
とする。
観測ベクトルに対して
を定義する。に比して
が小さければそのモデルのデータへの適合度が高いと言える。
これらの間には
が成り立つ。ここでであり、
の最も左の列はすべて
である。またすべての成分が
であるようなベクトルおよびそれの定数倍のベクトルも固有値
の固有ベクトルになり、
が成立する。したがって
も成り立つ。
次にベクトルの両辺で大きさの二乗を取ることで
が成り立つ。したがってである。
さらにと
が独立であることも示すことができる。実際
である。そしてに注意すれば
である。ともに正規分布に従うから、したがって両者は独立である。
指標
を決定係数という。単回帰()のときには決定係数は
の二乗に等しい。この意味で決定係数は説明変数と目的変数の相関の大きさを表していると考えられる。実際、および
より
が成り立つ。したがって
および
より
を得る。
また調整済み決定係数という、分子のと分母の
をそれぞれ自由度で割ったものに置き換えた
が用いられることもある。これはが大きくなればなるほど普通の決定係数が大きくなることを踏まえ、変数が大きくなると決定係数が小さくなるような罰則を課した決定係数に定義し直したものである。
決定係数は、説明変数によって目的変数がどれだけ説明できているかを表す。他方で説明変数同士に冗長なものが無いかを測る尺度としてがある。
番目の説明変数の
は
である。ここでは目的変数として
の第
列を、説明変数としてそれ以外の変数を用いたときの重回帰における決定係数である。
はその説明変数の他の変数に対する共線性を検出するものである。
1.7.1 決定係数のシミュレーション結果(R)
########################## ### 決定係数を定義する ### ########################## # 決定係数を与える関数 R2 <- function(vc_x,vc_y){ vc_y_hat <- lm(formula(vc_y~vc_x))$fitted.values # y_hat vc_y_bar <- mean(vc_y) # y_bar # TSS, RSSを定義 nm_RSS <- sum((vc_y - vc_y_hat)^2) nm_TSS <- sum((vc_y - vc_y_bar)^2) return(1-nm_RSS/nm_TSS) } # 調整済み決定係数 R2_adj <- function(vc_x,vc_y){ vc_y_hat <- lm(formula(vc_y~vc_x))$fitted.values # y_hat vc_y_bar <- mean(vc_y) # y_bar # TSS, RSSを定義 nm_RSS <- sum((vc_y - vc_y_hat)^2) nm_TSS <- sum((vc_y - vc_y_bar)^2) # 自由度を調整する nm_TSS <- nm_TSS/(nrow(vc_x)-1) nm_RSS <- nm_RSS/(nrow(vc_x)-ncol(vc_x)-1) # 返り値 return(1-nm_RSS/nm_TSS) } # テストデータを作成 nm_sim <- 10000 # シミュレーション数 nm_n <- 500 # 標本数 nm_m <- 1 # 説明変数の数 # テスト結果を格納 df_result_1 <- data.frame(matrix(nrow = 3, ncol = nm_sim)) rownames(df_result_1) <- c("R^2","rho^2","AE") colnames(df_result_1) <- 1:nm_sim for(i in 1:nm_sim){ set.seed(i) vc_x <- matrix(rnorm(nm_n * nm_m), ncol = nm_m) vc_y <- rnorm(nm_n) # 決定係数を計算 df_result_1[,i] <- c(R2(vc_x,vc_y), as.numeric(cor(vc_x,vc_y)^2), R2(vc_x,vc_y) - as.numeric(cor(vc_x,vc_y)^2)) } ret <- c(apply(df_result_1,1,mean),apply(df_result_1,1,sd)) # 説明変数を増やすとどうなるか調べてみる nm_max_var <- 500 # 説明変数の数の上限 vc_result <- c() vc_result_adj <- c() for(nm_m in 1:nm_max_var){ vc_x <- matrix(rnorm(nm_n * nm_m), ncol = nm_m) vc_y <- rnorm(nm_n) # 決定係数を計算 vc_result <- c(vc_result,R2(vc_x,vc_y)) vc_result_adj <- c(vc_result_adj,R2_adj(vc_x,vc_y)) }
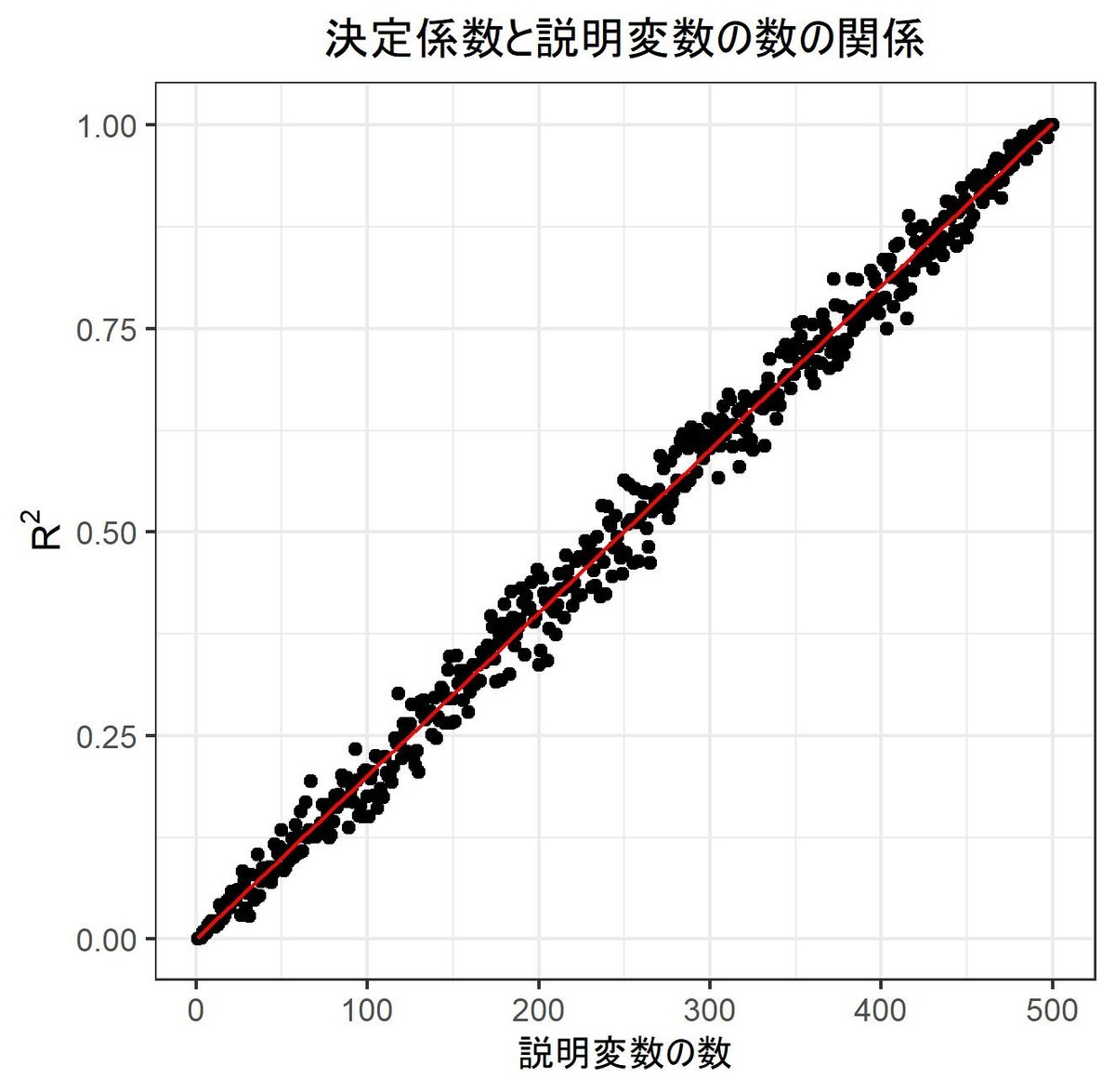
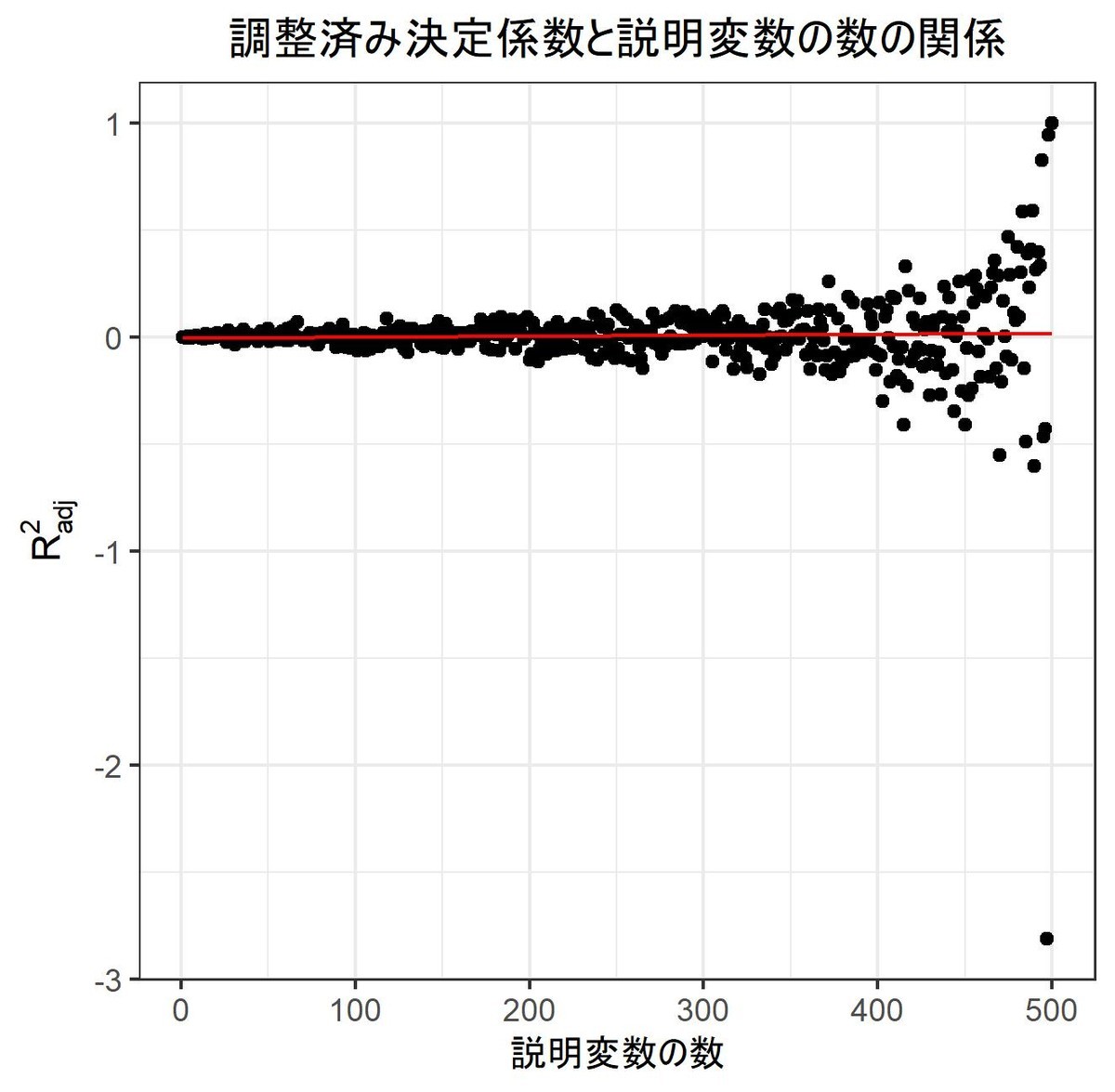
テスト結果
 |
 |
1.7.2 決定係数のシミュレーション結果(Python)
import numpy as np # 決定係数R^2を定義する def R2(x,y): n = x.shape[0] xx = np.insert(x, 0, 1, axis = 1) beta = np.linalg.inv(xx.T@xx)@xx.T@y y_hat = xx@beta y_bar = np.mean(y) RSS = np.linalg.norm(y - y_hat)**2 TSS = np.linalg.norm(y - y_bar)**2 return 1 - RSS/TSS # シミュレーションを実施 n = 300 m = 1 x = np.random.randn(n,m) y = np.random.randn(n) # 決定係数 print(R2(x,y)) # 相関係数の二乗 xx = x.reshape(n) print(np.corrcoef(xx,y)[0,1]**2) # 絶対誤差 print(R2(x,y) - np.corrcoef(xx,y)[0,1]**2)
1.7.3 VIFのシミュレーション(R)
##################### ### VIFを計算する ### ##################### R2 <- function(vc_x,vc_y){ vc_y_hat <- lm(formula(vc_y~vc_x))$fitted.values # y_hat vc_y_bar <- mean(vc_y) # y_bar # RSS, TSSを定義 nm_RSS <- sum((vc_y - vc_y_hat)^2) nm_TSS <- sum((vc_y - vc_y_bar)^2) return(1-nm_RSS/nm_TSS) } VIF <- function(vc_x){ p <- ncol(vc_x) vc_values <- array(dim = p) for(j in 1:p){ vc_values[j] <- 1/(1 - R2(vc_x[,-j],vc_x[,j])) } return(vc_values) } library("MASS") x <- as.matrix(Boston) VIF(x)
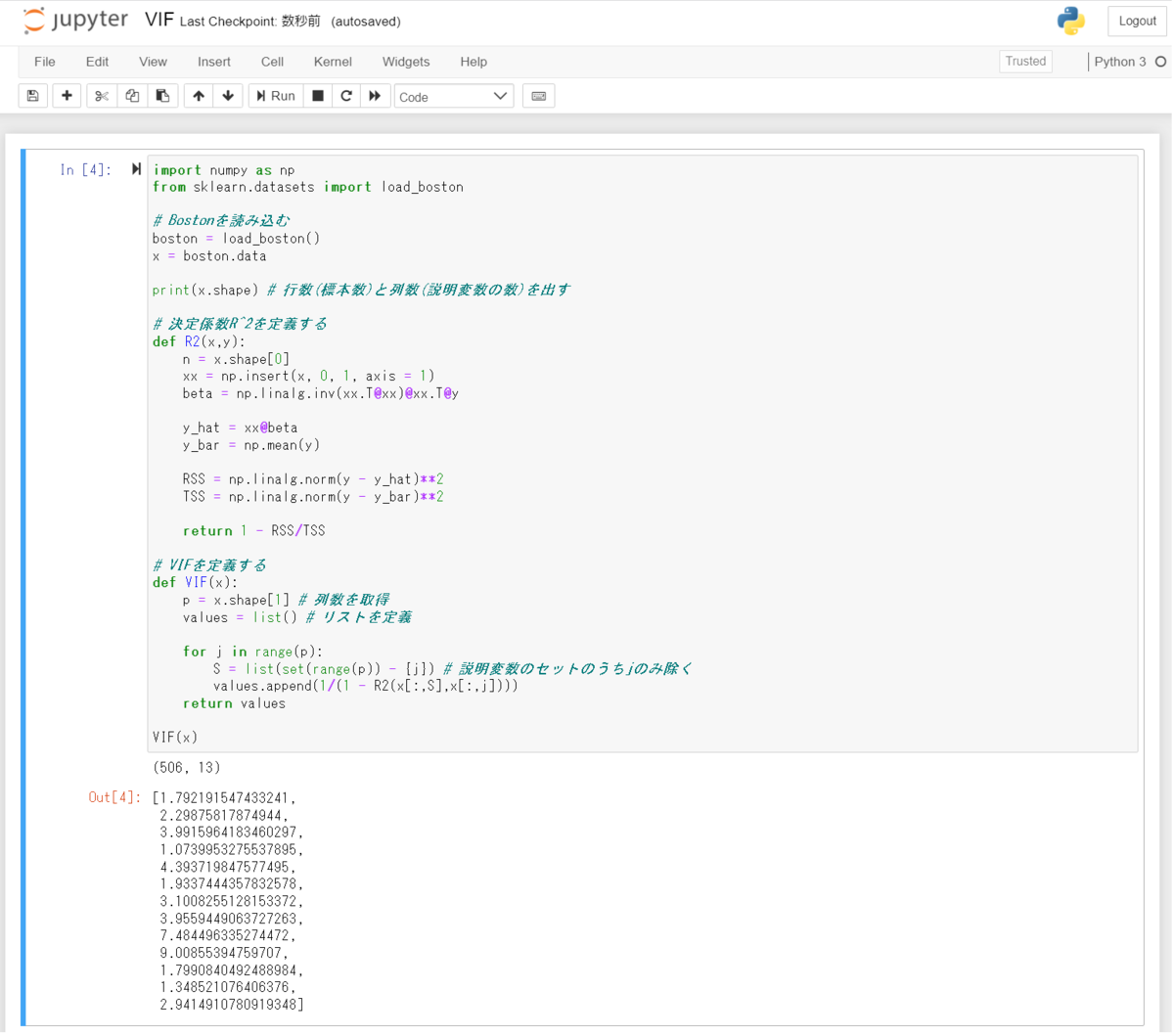
1.7.4 VIFのシミュレーション(Python)
import numpy as np from sklearn.datasets import load_boston # Bostonを読み込む boston = load_boston() x = boston.data print(x.shape) # 行数(標本数)と列数(説明変数の数)を出す # 決定係数R^2を定義する def R2(x,y): n = x.shape[0] xx = np.insert(x, 0, 1, axis = 1) beta = np.linalg.inv(xx.T@xx)@xx.T@y y_hat = xx@beta y_bar = np.mean(y) RSS = np.linalg.norm(y - y_hat)**2 TSS = np.linalg.norm(y - y_bar)**2 return 1 - RSS/TSS # VIFを定義する def VIF(x): p = x.shape[1] # 列数を取得 values = list() # リストを定義 for j in range(p): S = list(set(range(p)) - {j}) # 説明変数のセットのうちjのみ除く values.append(1/(1 - R2(x[:,S],x[:,j]))) return values VIF(x)