を参照していく。
5. データの探索
5.3 探索のためのデータ構造
ソートされた配列に対するデータ探索は、配列のまま行うとデータの挿入や全体の並び替えに時間がかかる。そこで配列ではなく木構造で保持することで探索と挿入を柔軟に行うことができる。
5.3.1 木構造
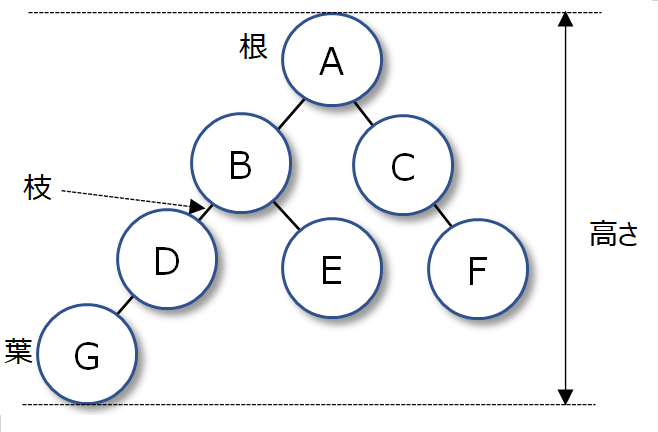 |
木はノードおよび枝からなる。最も上位になるノードを根といい、最も下位のノードを葉という。あるノードの下にあるノードをそのノードの子コードという。根からあるノードまでの距離を深さという。たとえば上図のDの深さは2である。根から葉までの深さを高さという。ノードにはいくつも子コードがあっても問題ない。特に全ノードの子コードが高々2個である場合、二分木という。
5.3.2 二分探索木
二分木を用いたデータ構造の表現を考える。各ノードに値を保持した二分木を作る。以下のように親ノードの値が子ノードよりも大きく、より左側にある値は右側の値よりも小さいという値の配置を満たす二分木を二分探索木という。
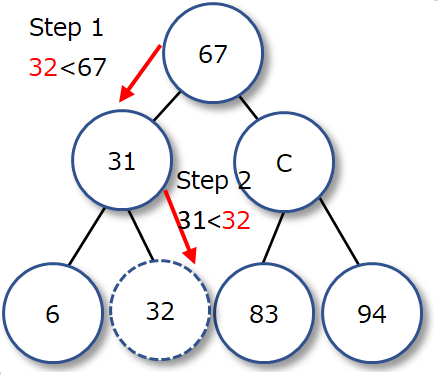 |
二分探索木によるデータの挿入を考える。まず根から始める。根に格納された値と挿入する値を比較する。もし挿入値が格納値よりも小さければ、根の値よりも値の小さい方の子ノードへ移り、そうでなればより大きい方の子ノードへ移る。次に移った子ノードの値と挿入値を比較する。これを延々と繰り返し、葉の直前のノードにおいて比較を行った結果として子ノードが無かったならば、挿入値を新たな子ノードとする。これによりデータ挿入ができる。
二分探索木を用いた場合の計算量を考える。要素の個数をとするとき、計算の各ステップは要素の比較であり、最悪の場合で気の高さに相当する
回の比較を行うから
である。二分探索木の高さ
と要素数
の間には
が成り立つから、計算量を
を用いて書き換えることで
を得る。これに対してソート済のような配列を対応させた、ノードが一直線に並ぶ木をつくると高さが
になり探索に掛かる計算量も
になる。
Pythonで実装させると以下のとおりになる:
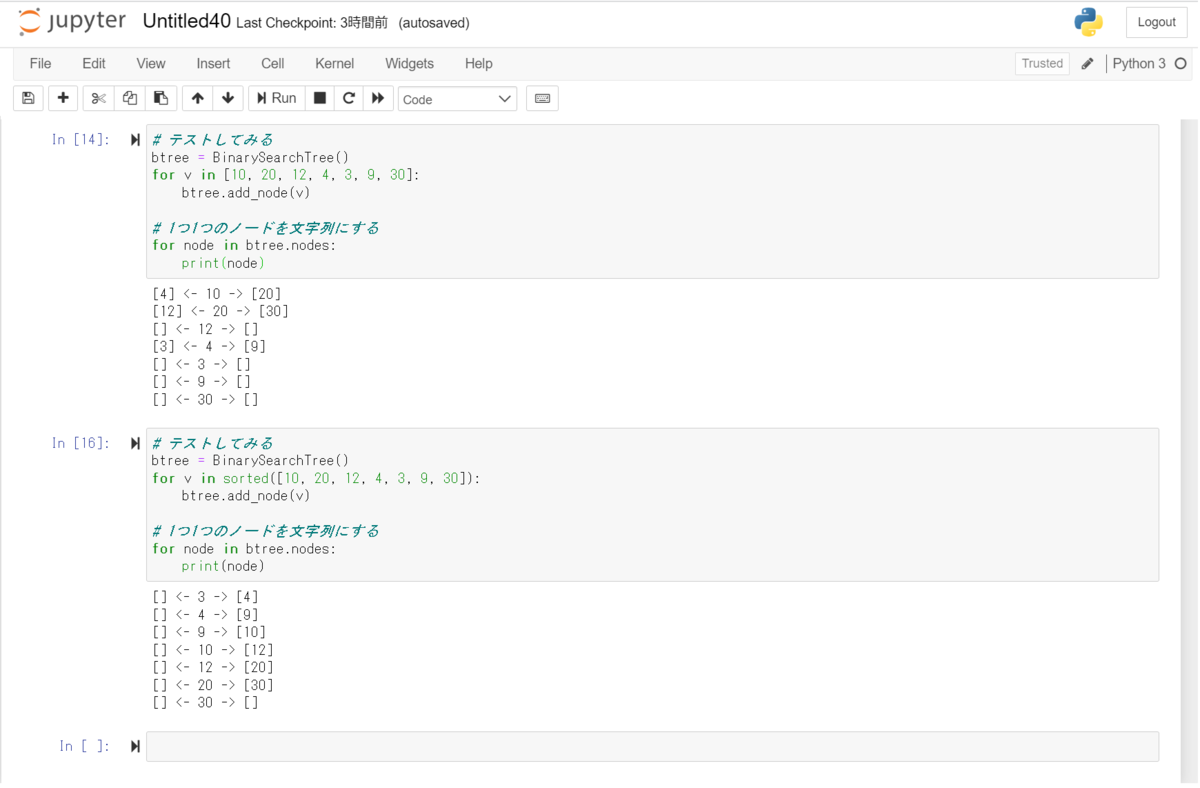
class Node: def __init__(self, value): self.value = value self.left = None self.right = None def __str__(self): left = f'[{self.left.value}]' if self.left else '[]' right = f'[{self.right.value}]' if self.right else '[]' return f'{left} <- {self.value} -> {right}' class BinarySearchTree: def __init__(self): self.nodes = [] def add_node(self, value): node = Node(value) if self.nodes: # 自分の親ノードを探す parent, direction = self.find_parent(value) if direction == 'left': parent.left = node else: parent.right = node # この木のノードとして格納 self.nodes.append(node) def find_parent(self, value): node = self.nodes[0] # nodeがNoneになるまでループさせる while node: p = node # 戻り値の候補として保存しておく if p.value == value: raise ValueError('The value already included is not accepted.') if p.value > value: direction = 'left' node = p.left else: direction = 'right' node = p.right return p, direction # テストしてみる btree = BinarySearchTree() for v in [10, 20, 12, 4, 3, 9, 30]: btree.add_node(v) # 1つ1つのノードを文字列にする for node in btree.nodes: print(node)
 |
5.3.2 木のバランス
二分探索木を用いたデータの探索ないし新たな値の挿入がの計算量で出来るのは1ステップの計算を終えるたびに探索対象のサイズが半分になることに起因していた。そのため二分探索木の形が左右にバランスよく作られている必要がある(このような木を均衡木という。)。
