を参照していく。
前回
8. 問題の難しさ
8.1 計算に掛かるコスト
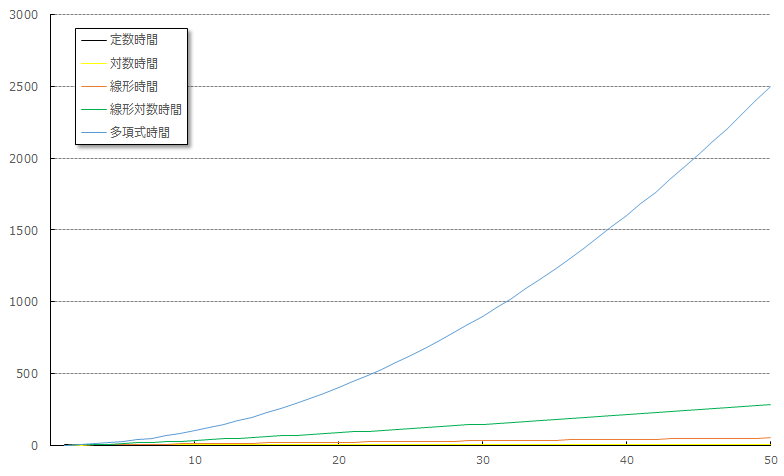
8.1.1 計算時間の変化
| 1. 定数時間 | 要素の数に寄らずに一定時間しかかからない計算量 | |
|---|---|---|
| 2. 対数時間 | ソートされた配列内の目的値を二分探索で探索する際などで掛かる計算量 | |
| 3. 線形時間 | 要素数の定数倍のステップ数を必要とする計算量 | |
| 4. 線形対数時間 | 線形時間と対数時間の積だけ掛かる計算量 | |
| 5. 多項式時間 | 要素数の多項式で表される計算量。 |
8.1.4 メモリに関するコスト
アルゴリズムの実行に際して必要となるメモリを空間複雑性という。一般に計算の複雑性を考える場合、時間と空間(メモリ)の双方を考える必要がある。
のリストはそのサイズを任意に変更できるため、
言語よりはメモリを気にしなくともよいが、大規模なプログラムや速度を求められる場合にはこうした要素を考慮しなければならない。
8.2 難しさの分類
8.2.1 コンピュータのモデル
プログラムを実行して問題を解く現代のコンピュータはチューリング機械()と呼ばれる数学的なモデルを基盤としている。ここでは詳述しないが、プログラムを実行し、分岐がある場合はいずれか1つの道筋を選んで計算を続ける機械を指す。
多項式時間で解けるアルゴリズムを持たない問題を難しい問題()と呼ぶことにする。チューリング機械を拡張して計算途中にある分岐を1回の実行ですべて計算できる理論的なものを非決定的チューリング機械と呼ぶ*2
8.2.2 PとNP
配列のソートやグラフの最短距離を求める問題は、多項式時間で解くことができる。こうした多項式時間で解ける問題をクラスというこれに対して普通のコンピュータでは多項式時間で解けないものの、非決定的チューリング機械では多項式時間で解ける問題をクラス
という。
問題がクラスであるためには判定問題である必要がある。すなわちその問いに対する解答が
または
であるようなものでなければならない。
8.2.3 3SAT
クラスである例として
を考える。
または
を保持する変数がいくつかあるとする。またそれらの否定を考え、これらをまとめてリテラルと呼ぶこととする。リテラルを複数並べて論理和でつなげたものを節と呼ぶ。この節をいくつか並べて論理積で繋げたもののうち、全体で
となる変数の組み合わせが存在するかを判定する問題を
という。
############ ### kSAT ### ############ import random random.seed(8) class kSAT: @classmethod def generate(cls, k, var_num, clause_num): """変数の数(var_num)と節の数(clause_num)からkSAT問題を作る""" ksat = cls() var_list = list(range(var_num)) # 問題の本体を格納するための変数 res = [] while len(res) < clause_num: clause = [] # 高々k個の変数が含まれる clause_size = random.randint(1, k) for i in random.sample(var_list, clause_size): # 1ならばnotで変数を否定する prefix = random.choice((0, 1)) clause.append((prefix, i)) # 同一の節を判定できるように変数の添え字でソート clause.sort(key = lambda x: x[1]) if clause not in res: res.append(clause) # kSATのインスタンスに格納 ksat.body = res return ksat def test(self, var_list): """受け取ったvar_listのTrue, Falseを用いて論理式を評価する""" res = [] for clause in self.body: clause_data =[not var_list[i] if p else var_list[i] for p,i in clause] res.append(any(clause_data)) return all(res) def __str__(self): res = [] for clause in self.body: clause_str = [f'¬x{i}' if p else f'x{i}' for p,i in clause] res.append('(' + '∧'.join(clause_str) + ')') return '∧'.join(res) ##### ksat = kSAT.generate(3, 4, 3) print(ksat) ##### while True: cand = random.choices([True, False], k=4) if ksat.test(cand): print(cand) break
