を参照していく。
前回
7. 問題を解くための技術
ナップサック問題を3通りの方法で解いてみる。
7.1 ナップサック問題
出張や旅行で、異なる重量のお土産を重量制限ギリギリまでなるべく多く*1収めるためにどれをどれだけ収納するかを解く問題をナップサック問題という。
7.1.1 ナップサック問題の概要
重量に制限(上限)があるナップサックが1つある。他方で個の品物があり、それぞれの品物には重さと値段がある(いずれも正の整数とする。)。品物にはラベル(名前か番号)を付けて区別する。これらの品物をナップサックに詰めるときに、重量制限を守りつつ、ナップサック内にある品物の価値が最大になるような組み合わせを求めたい。これがナップサック問題である。ここでは各品物は1単位を入れるか入れないかの2択だとする*2。
以下ではすべての品物の重さと値段が異なるものとする。
まずはテスト用に品物リストを乱数で生成する。各品物の重さ上限はkg、品物の個数は
個、価値の上限は
万円とする。
################################## ### 品物リストを乱数で作成する ### ################################## from collections import namedtuple import random random.seed(7)# 乱数シード # クラスを作成: Item = namedtuple('Item', ('name', 'weight', 'price')) # 品物の個数 num = 20 # 品物を保持するリスト item_list = [] max_weight = 5 # 重さの上限値:乱数で発生させるため # 品物の個数よりも大きな数値にする max_price = 50 # 値段の候補リストを作り、シャッフルする price_list = list(range(1, max_price + 1)) random.shuffle(price_list) # 無作為に品物を作る。名前は番号 for i in range(num): w = random.randint(1, max_weight) item = Item(i, w, price_list.pop()) item_list.append(item) item_list
また今後のためにナップサックを表現するクラスを定義しておく。
######################## ### 各種クラスを定義 ### ######################## class Knapsack: def __init__(self, size): # このナップサックが保持できる最大の重さ self.size = size # 現在の重さ self.weight = 0 # 入っている品物の価値の総和 self.value = 0 # 保持するItemの配列 self.items = [] def append(self, item): """ このナップサックにItemを追加する """ if not self.has_room_for(item): raise ValueError('この品物は入れられません。重量オーバーです。') self.items.append(item) self.weight += item.weight self.value += item.price def has_room_for(self, item): """ 引数に取った品物を入れる余裕があるかを真偽値で返す """ return self.size >= self.weight + item.weight def __str__(self): val = '重さ {} kg / 価値 {} 万円'.format(self.weight, self.value) return val
7.1.2 貪欲法
解き方としても最も単純な貪欲法()を考える。これは同じ重さならばより価値があるものを持って帰るだろうと考え、値段を重さで割った値*3で品物を降順に並べ替え、その値が高いものから順にすべての品物についてナップサックに入るかどうかを試す。
def greedy(items, size_limit): # 単位重さ当たりの値段で品物を並び替える sorted_item_list = sorted(items, key = lambda x: x.price/x.weight, reverse = True) my_knapsack = Knapsack(size_limit) for v in sorted_item_list: # 入る余地があるならば品物を入れる try: my_knapsack.append(v) except ValueError: continue return my_knapsack knap_g = greedy(item_list, 40) print(knap_g)
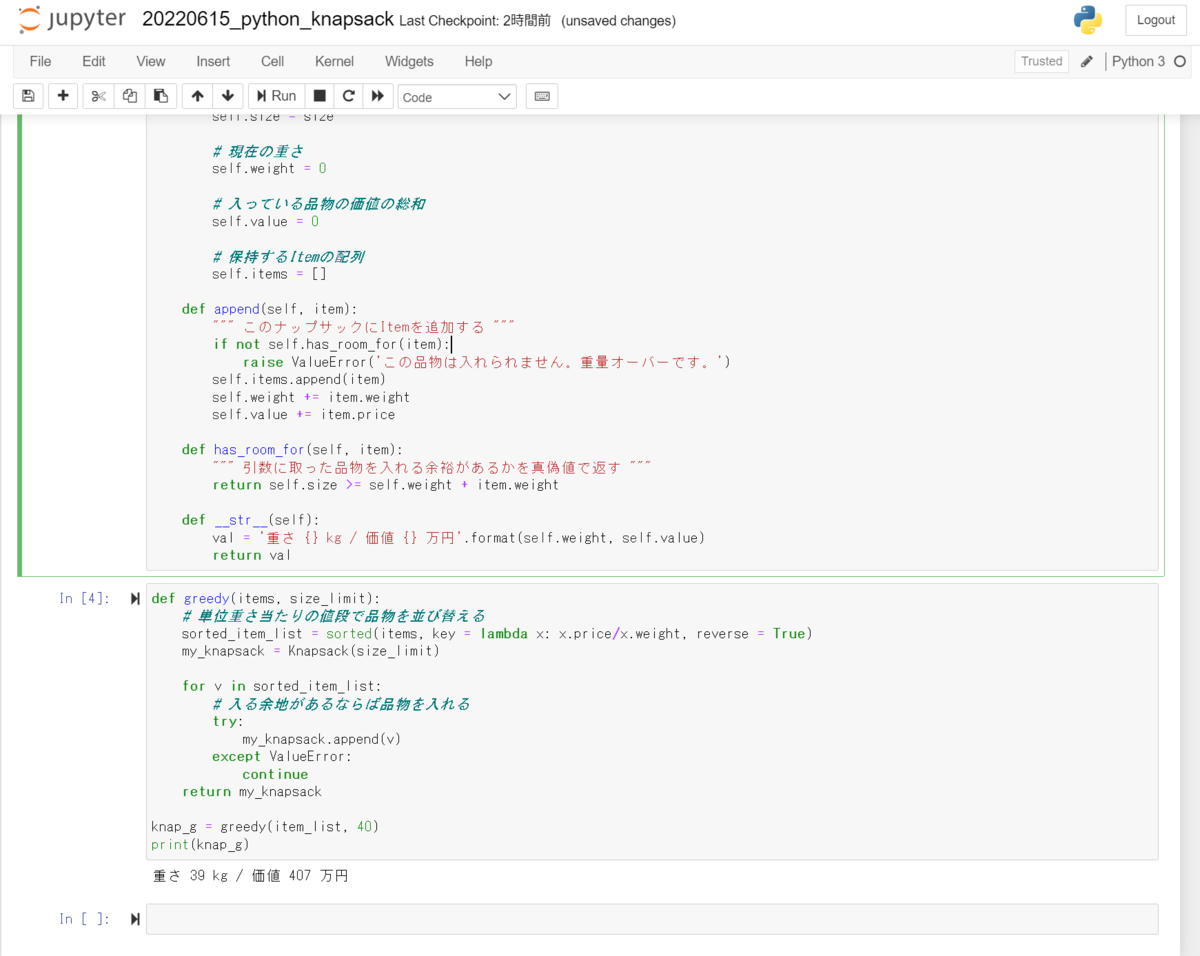 |
7.1.3 総当たり
品物は全部で個あり、各品物は入るか否かの2択であるから、ナップサックへの詰め方は
通りある。これをすべて調べる。そのうちナップサックの重量を超えているものを除外する。残った品物の組み合わせのうち最も価値のあるものが最適な解になる。これを
-
アルゴリズムという。
import itertools def brute_force(items, size_limit): # 答えの候補 candidate = None for pattern in itertools.product((0,1), repeat = len(items)): my_box = [] for i, val in enumerate(pattern): if val: my_box.append(item_list[i]) w = sum([item.weight for item in my_box]) # ナップサックの重量制限を守れないならば、ループの次へ if w > size_limit: continue # 総額を計算しこれまでの最高を上回るのであれば、候補として残す value = sum([item.price for item in my_box]) if candidate is None or value > candidate.value: knapsack = Knapsack(size_limit) for v in my_box: knapsack.append(v) candidate = knapsack return candidate knap_bf = brute_force(item_list, 40) print(knap_bf)
