統計的機械学習の数理100問（15/20） - 「大人の教養・知識・気付き」を伸ばすブログ

　いい加減時代の潮流に乗ろうということで機械学習を学びたいと思う。またRはともかくとしてPythonは未経験であるため、丁度良い書籍として

統計的機械学習の数理100問 with R (with R) (機械学習の数理100問シリーズ)

作者:讓, 鈴木
共立出版

Amazon

統計的機械学習の数理100問 with Python (機械学習の数理100問シリーズ)

作者:讓, 鈴木
共立出版

Amazon

を用いることにする。

前回
6.　非線形回帰
次回

前回

power-of-awareness.com

6.　非線形回帰

説明変数と目的変数の関係が非線形の場合を検討する。

スプライン回帰を考える。

6.1　多項式回帰

　標本 $X_1,Y_1),\cdots,(X_n,Y_n)\in\mathbb{R}^2$ を多項式に当てはめることを検討する。最小二乗法と同様に

$\begin{aligned} \displaystyle{\sum_{i=1}^{n}\{Y_i-(\beta_0+\beta_1X_i+\cdots+\beta_p X_i^p)\}^2} \end{aligned}$

を最小にするような係数 $\beta_0,\beta_1,\cdots,\beta_p$ を求めるものとする。
　これは通常の重回帰モデルにおいて各説明変数を冪乗に置き換えたものに他ならないから、

$\begin{aligned} X=\begin{bmatrix} 1&X_1&\cdots&X_1^p\\ \vdots&\vdots&\ddots&\vdots\\ 1&X_n&\cdots&X_n^p \end{bmatrix} \end{aligned}$

とおけば、 ${}^{t}XX$ が正則ならば、 $\hat{\boldsymbol{\beta}}=({}^{t}XX)^{-1}{}^{t}X\boldsymbol{Y}$ が解となる。ここで $\boldsymbol{Y}={}^{t}(Y_1,\cdots,Y_p)$ とおいた。

6.2　スプライン回帰

　次数が高々 $3$ 次*1であるような $x$ に関する多項式関数 $f,g$ が、ある点 $x_{*}\in\mathbb{R}$ で二次微分までがすべて等しいとき、

$\begin{aligned} f(x)&=\displaystyle{\sum_{j=0}^{3}\beta_j(x-x_{*})^j},&\\ &&\Rightarrow \beta_j=\gamma_j,j=0,1,2\\ g(x)&=\displaystyle{\sum_{j=0}^{3}\gamma_j(x-x_{*})^j}& \end{aligned}$

が成立する。
　これを踏まえて、定義域を複数の期間に分割し各期間に適当な3次関数(曲線)を当てはめる回帰手法をスプライン回帰という。すなわち区間を $[\alpha_0,\alpha_1]\times[\alpha_1,\alpha_2]\times\cdots$ $\times[\alpha_{k},\alpha_{k+1}]$ と分割し、

$\begin{aligned} f(x)&=\begin{cases} \beta_1+\beta_2 x+\beta_3 x^2+\beta_4 x^3,&\alpha_0\leq x\leq \alpha_1,\\ \beta_1+\beta_2 x+\beta_3 x^2+\beta_4 x^3+\beta_5(x-\alpha_1)^3,&\alpha_1\leq x\leq \alpha_2,\\ \beta_1+\beta_2 x+\beta_3 x^2+\beta_4 x^3+\beta_5(x-\alpha_1)^3+\beta_6(x-\alpha_2)^3,&\alpha_2\leq x\leq \alpha_3,\\ \vdots&\vdots\\ \beta_1+\beta_2 x+\beta_3 x^2+\beta_4 x^3+\beta_5(x-\alpha_1)^3+&\\ \beta_6(x-\alpha_2)^3+\cdots+\beta_{k+4}(x-\alpha_k)^3,&\alpha_k\leq x\leq \alpha_{k+1} \end{cases}\\ &=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\displaystyle{\sum_{i=1}^{k}\beta_{i+3}(\max\{x-\alpha_i,0\})^3} \end{aligned}$

とおく。
　係数 $\beta_1,\cdots,\beta_{k+4}$ はこれまでと同様の手順で推定できる。観測標本 $(x_1,y_1),\cdots,(x_n,y_n)$ が与えられているとき、

$\begin{aligned} X=\begin{bmatrix} 1 &x_1 &x_1^2 &x_1^3&(\max\{x_1-\alpha_1,0\})^3&\cdots&(\max\{x_1-\alpha_k,0\})^3\\ 1 &x_2 &x_n^2 &x_2^3&(\max\{x_2-\alpha_1,0\})^3&\cdots&(\max\{x_2-\alpha_k,0\})^3\\ \vdots&\vdots&\vdots&\vdots&\vdots &\vdots&\vdots\\ 1 &x_n &x_n^2 &x_n^3&(\max\{x_n-\alpha_1,0\})^3&\cdots&(\max\{x_n-\alpha_k,0\})^3 \end{bmatrix} \end{aligned}$

とするとき、平均二乗誤差

$\begin{aligned} \displaystyle{\sum_{i=1}^{n} \left[y_i-\left\{\beta_1+\left(\sum_{j=2}^{4}\beta_j x_i^{j}\right)+\sum_{l=1}^{k}(\max\{x_i-\alpha_l,0\})^3\beta_{l+4}\right\}\right]}^2 \end{aligned}$

が最小になるような $\boldsymbol{\beta}={}^{t}(\beta_1,\cdots,\beta_{k+4})$ を求めればよい。 $X$ の階数が $k+4$ であれば ${}^{t}XX$ は正則であり、 $\hat{\boldsymbol{\beta}}=({}^{t}XX)^{-1}{}^{t}X\boldsymbol{y}$ で求まる。

6.3　自然なスプライン関数への回帰

　自然なスプライン関数は $\alpha_1\leq x\leq \alpha_k$ の $k-1$ 個に分割された区間で2次曲線、両端 $x\leq\alpha_1,\alpha_k\leq x$ で直線に回帰するスプライン関数の変種である。

$\begin{aligned} f(x)=\begin{cases} \beta_1+\beta_2 x,&\alpha_0\leq x\leq \alpha_1\\ \beta_1+\beta_2 x+\beta_3(x-\alpha_1)^3,&\alpha_0\leq x\leq \alpha_1\\ \vdots\\ \beta_1+\beta_2 x+\beta_3(x-\alpha_1)^3+\cdots+\beta_k(x-\alpha_{k-2})^3,&\alpha_0\leq x\leq \alpha_1\\ \beta_1+\beta_2 x+\beta_3(x-\alpha_1)^3+\cdots+\beta_k(x-\alpha_{k-2})^3+\beta_{k+1}(x-\alpha_{k-1})^3,&\alpha_0\leq x\leq \alpha_1 \end{cases} \end{aligned}$

の $x=\alpha_k$ における2回微分が $0$ であるから、 $\displaystyle{6\sum_{j=3}^{k+1}\beta_j(\alpha_k-\alpha_{j-2}) }=0$ が成立するから、

$\begin{aligned} \beta_{k+1}=-\displaystyle{\sum_{j=3}^{k}\frac{\alpha_k-\alpha_{j-2}}{\alpha_k-\alpha_{k-1}}\beta_j} \end{aligned}$

を得る。これにより直線部分も一意に求まる。したがって関数 $f$ は $\beta_1,\cdots,\beta_k$ を指定すれば定まる。

自然スプラインの推定量　関数 $f(x)$ は $k$ 個の多項式 $h_1(x)=1,h_2(x)=x,$ $h_{j+2}(x)=d_j(x)-d_{k-1}(x),$ $j=1,\cdots,k-2$ を基底に持ち、各 $\beta_1,\cdots,\beta_k$ に対して

$\begin{aligned} \gamma_1&=\beta_1,\gamma_2=\beta_2,\gamma_3=(\alpha_k-\alpha_1)\beta_3,\\ \gamma_i&=(\alpha_k-\alpha_{i-2})\beta_i,\gamma_k=(\alpha_k-\alpha_{k-2})\beta_k \end{aligned}$

と対応付けると、 $f(x)=\displaystyle{\sum_{j=1}^{k}\gamma_j h_j(x)}$ とできる。ただし

$\begin{aligned} d_j(x)=\displaystyle{\frac{(\max\{x-\alpha_j,0\})^3-(\max\{x-\alpha_k,0\})^3}{\alpha_k-\alpha_j}},j=1,\cdots,k-1 \end{aligned}$

とおいた。

( $\because$ 　まず

$\begin{aligned} \beta_{k+1}=-\displaystyle{\sum_{j=3}^{k}\frac{\alpha_k-\alpha_{j-2}}{\alpha_k-\alpha_{k-1}}\beta_j} \end{aligned}$

は $\gamma_{k+1}=(\alpha_k-\alpha_{k-1})\beta_{k+1}$ とおけば

$\begin{aligned} \gamma_{k+1}=-\displaystyle{\sum_{j=3}^{k}\gamma_j} \end{aligned}$

と書き換えることができる。
　 $x\leq\alpha_k$ について、

$\begin{aligned} \displaystyle{\sum_{j=3}^{k+1}\gamma_j\frac{(\max\{x-\alpha_{j-2}\})^3}{\alpha_k-\alpha_{j-2}}}&=\displaystyle{\sum_{j=3}^{k}\gamma_j\frac{(\max\{x-\alpha_{j-2}\})^3}{\alpha_k-\alpha_{j-2}}}-\displaystyle{\sum_{j=3}^{k}\gamma_j\frac{(\max\{x-\alpha_{k-1}\})^3}{\alpha_k-\alpha_{k-1}}}\\ &=\displaystyle{\sum_{j=3}^{k}\gamma_j\left\{\frac{(\max\{x-\alpha_{j-2}\})^3}{\alpha_k-\alpha_{j-2}}-\frac{(\max\{x-\alpha_{k-1}\})^3}{\alpha_k-\alpha_{k-1}}\right\}}\\ &=\displaystyle{\sum_{j=3}^{k}\gamma_j(d_{j-2}(x)-d_{k-1}(x))} \end{aligned}$

が成り立つから、

$\begin{aligned} f(x)&=\beta_1+\beta_2x+\displaystyle{\sum_{j=3}^{k+1}\beta_j(x-\alpha_{j-2})^3}\\ &=\gamma_1+\gamma_2x+\displaystyle{\sum_{j=3}^{k+1}\gamma_j\frac{(\max\{x-\alpha_{j-2}\})^3}{\alpha_k-\alpha_{j-2}}}\\ &=\gamma_1+\gamma_2x+\displaystyle{\sum_{j=3}^{k}\gamma_j(d_{j-2}(x)-d_{k-1}(x))}\\ &=\displaystyle{\sum_{j=1}^{k}\gamma_jh_j(x)} \end{aligned}$

が得られる。
　他方で $x\geq\alpha_k$ では $j=1,\cdots,k-2$ について

$\begin{aligned} h_{j+2}(x)=&\displaystyle{\frac{(x-\alpha_j)^3-(x-\alpha_k)^3}{\alpha_k-\alpha_j}}-\displaystyle{\frac{(x-\alpha_{k-1})^3-(x-\alpha_k)^3}{\alpha_k-\alpha_{k-1}}}\\ =&\displaystyle{\frac{-3(\alpha_j-\alpha_k)x^2+3(\alpha_j^2-\alpha_k^2)x-(\alpha_j^3-\alpha_k^3)}{\alpha_k-\alpha_j}}\\ &-\displaystyle{\frac{-3(\alpha_{k-1}-\alpha_k)x^2+3(\alpha_{k-1}^2-\alpha_k^2)x+(\alpha_{k-1}^3-\alpha_k^3)}{\alpha_k-\alpha_{k-1}}}\\ =&3x^2-3(\alpha_j+\alpha_k)x+(\alpha_j^2+\alpha_j\alpha_k+\alpha_k^2)\\ &-\{3x^2-3(\alpha_{k-1}+\alpha_k)x+(\alpha_{k-1}^2+\alpha_{k-1}\alpha_k+\alpha_k^2)\}\\ =&3x(\alpha_{k-1}-\alpha_j)+\{(\alpha_j^2+\alpha_j\alpha_k+\alpha_k^2)-(\alpha_{k-1}^2+\alpha_{k-1}\alpha_k+\alpha_k^2)\}\\ =&3x(\alpha_{k-1}-\alpha_j)+(\alpha_j^2-\alpha_{k-1}^2+(\alpha_j-\alpha_{k-1})\alpha_k)\\ =&(\alpha_{k-1}-\alpha_j)(3x-\alpha_j-\alpha_{k-1}-\alpha_k) \end{aligned}$

を得る。したがって $f(x)=\displaystyle{\sum_{j=1}^{k}\gamma_jh_j(x)},$ $f^{\prime}(x)=\displaystyle{\sum_{j=1}^{k}\gamma_jh_j^{\prime}(x)}$ に $x=\alpha_k$ を代入することで

$\begin{aligned} f(\alpha_k)&=\gamma_1+\gamma_2\alpha_k+\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_{k-1}-\alpha_{j-2})(2\alpha_k-\alpha_{j-2}-\alpha_{k-1})},\\ f^{\prime}(\alpha_k)&=\gamma_2+3\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_{k-1}-\alpha_{j-2})} \end{aligned}$

を得る。
　さらに $\gamma_1+\gamma_2x+\displaystyle{\sum_{j=3}^{k+1}\gamma_j\frac{(\max\{x-\alpha_{j-2}\})^3}{\alpha_k-\alpha_{j-2}}}$ を用いて、

$\begin{aligned} f(\alpha_k)&=\gamma_1+\gamma_2\alpha_k+\displaystyle{\sum_{j=3}^{k}\gamma_j\frac{(\alpha_k-\alpha_{j-2})^3}{\alpha_k-\alpha_{j-2}} }\\ &=\gamma_1+\gamma_2\alpha_k+\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_k-\alpha_{k-1})^2}\\ &=\gamma_1+\gamma_2\alpha_k+\displaystyle{\sum_{j=3}^{k}(\alpha_k-\alpha_{j-2})^2 }-\displaystyle{\sum_{j=3}^{k}(\alpha_k-\alpha_{k-1})^2 }\\ &=\gamma_1+\gamma_2\alpha_k+\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_{k-1}-\alpha_{j-2})(2\alpha_k-\alpha_{j-2}-\alpha_{k-1}) }\\ f^{\prime}(\alpha_k)&=\gamma_2+3\displaystyle{\sum_{j=3}^{k+1}\gamma_j\frac{(\alpha_k-\alpha_{j-2})^2}{\alpha_k-\alpha_{j-2}} }\\ &=\gamma_2+3\displaystyle{\sum_{j=3}^{k+1}\gamma_j(\alpha_k-\alpha_{j-2})}\\ &=\gamma_2+3\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_k-\alpha_{j-2})}-3\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_k-\alpha_{k-1})}\\ &=\gamma_2+3\displaystyle{\sum_{j=3}^{k}\gamma_j(\alpha_{k-1}-\alpha_{j-2})} \end{aligned}$

を得る。以上から命題が示された。　 $\blacksquare$ )

6.4　シミュレーション

6.4.1　Rによるシミュレーション例

#################
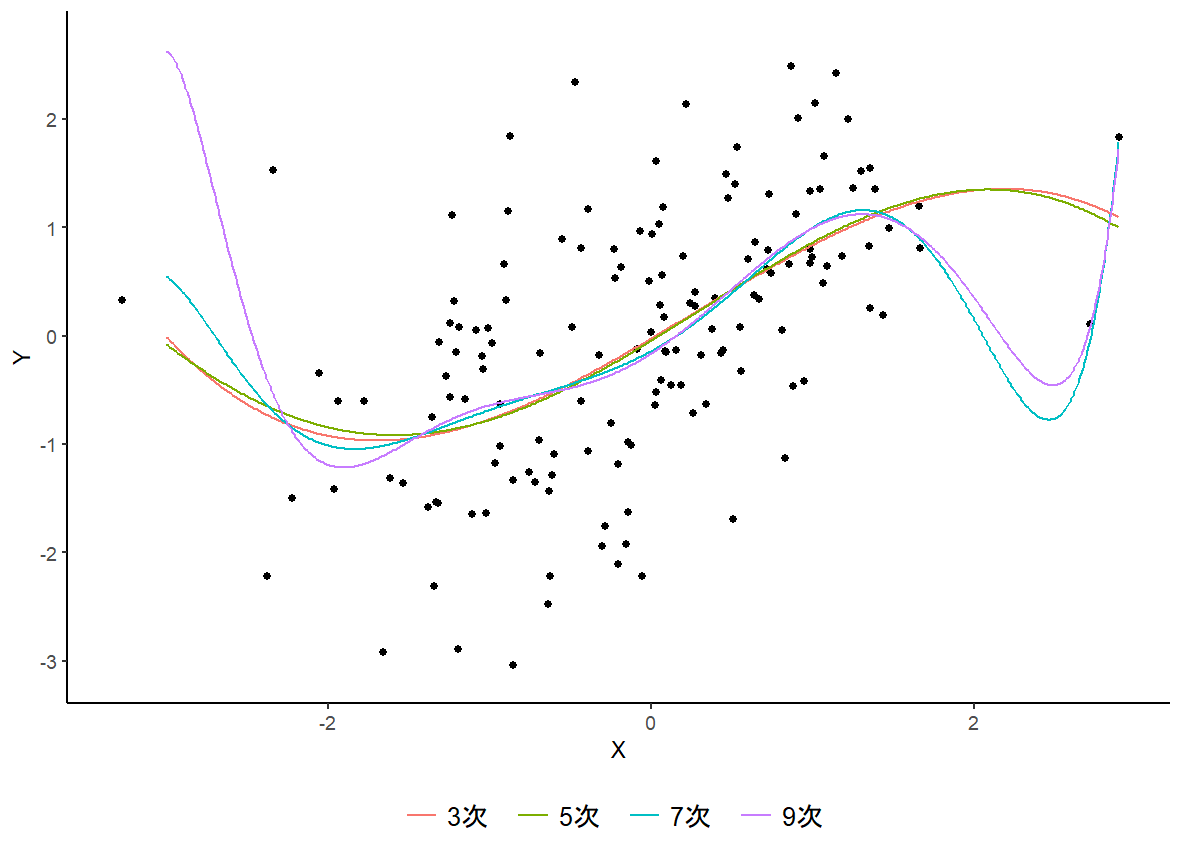
### 多項式回帰###
#################

# y=sin(x)+εでテストデータを生成

library("ggplot2")

n <- 150

# テストデータの生成
vc_x <- rnorm(n = n,mean = 0,sd = 1)
vc_y <- sin(x = vc_x) + rnorm(n = n,mean = 0,sd = 1)

# 次数データ
vc_p_set <- seq(3,9,2)
m <- length(vc_p_set)

# 次数を変えながら推定
for(i in 1:m){
  p <- vc_p_set[i]
  mt_x <- rep(1,n)
  
  for(j in 1:p){
    mt_x <- cbind(mt_x, vc_x^j)
  }
  
  # 母数の推定
  beta <- drop(solve(t(mt_x) %*% mt_x) %*% t(mt_x) %*% vc_y)

  # モデルによる予測値と比較する
  vc_x2 <- seq(-3,3,0.01)
  mt_x <- rep(1,length(vc_x2))
  
  for(j in 1:p){
    mt_x <- cbind(mt_x, vc_x2^j)
  }
  
  vc_y_pred <- as.vector(beta %*% t(mt_x))
  
  if(i==1){
    df_data <- data.frame(matrix(nrow = length(vc_y_pred), ncol = m + 1))
    colnames(df_data) <- c("x",paste0(vc_p_set,"次"))
    df_data[,1] <- vc_x2
    df_data[,2] <- vc_y_pred
  }else{
    df_data[,i+1] <- vc_y_pred
  }
}

df_data_graph <- data.frame(x = df_data[,1],
                            var = rep(colnames(df_data)[2],nrow(df_data)),
                            y = df_data[,2])

for(i in 3:ncol(df_data)){
  df_data_graph <- rbind(df_data_graph,data.frame(x = df_data[,1],
                                                  var = rep(colnames(df_data)[i],nrow(df_data)),
                                                  y = df_data[,i]))
}

df_data_org <- data.frame(x = vc_x, y = vc_y)


vc_x_lim <- c(min(vc_x)-0.05,max(vc_x)+0.05)
vc_x_lim <- round(vc_x_lim,digits = 1)

vc_y_lim <- c(min(c(df_data_org[,"y"],df_data_graph[(df_data_graph[,1]>=vc_x_lim[1])&(df_data_graph[,1]<=vc_x_lim[2]),3]))-0.05,
              max(c(df_data_org[,"y"],df_data_graph[(df_data_graph[,1]>=vc_x_lim[1])&(df_data_graph[,1]<=vc_x_lim[2]),3]))+0.05)
vc_y_lim <- round(vc_y_lim,digits = 1)




g <- ggplot(df_data_org,aes(x=x,y=y)) + geom_point()
g <- g + geom_line(data = df_data_graph,mapping = aes(x = x, y = y, color = var))
g <- g + xlab(label = "X") + ylab(label = "Y")
g <- g + labs(color = "")
g <- g + scale_x_continuous(limits = vc_x_lim)
g <- g + scale_y_continuous(limits = vc_y_lim)
g <- g + theme_classic() + theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom",
                                   legend.title=element_text(size = 7),
                                   legend.text=element_text(size = 12),
                                   legend.background = element_blank())
plot(g)

##################
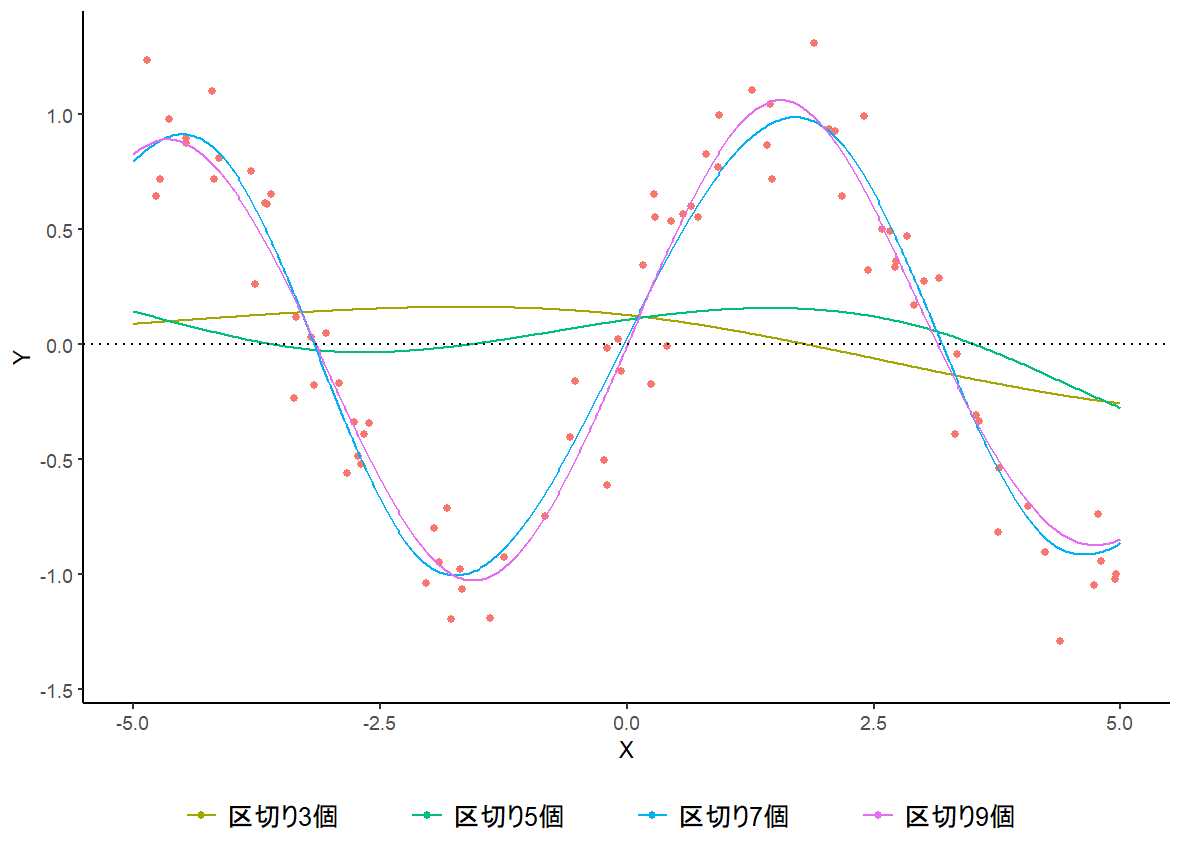
### スプライン ###
##################
n <- 150

vc_x <- rnorm(n) * 2 * pi
vc_y <- sin(vc_x) + 0.2 * rnorm(n)

# 区切り点の属性
vc_p_set <- seq(3,9,2)

for (k in 1:length(vc_p_set)){
  p <- vc_p_set[k]
  vc_knots <- seq(-2 * pi, 2 * pi, length = p)
  X <- matrix(nrow = n, ncol = p + 4)
  
  for (i in 1:n) {
    X[i, 1] <- 1
    X[i, 2] <- vc_x[i]
    X[i, 3] <- vc_x[i] ^ 2
    X[i, 4] <- vc_x[i] ^ 3
    for (j in 1:p){
      X[i, j + 4] <- max((vc_x[i] - vc_knots[j]) ^ 3, 0)
    }
  }
  
  vc_beta <- solve(t(X) %*% X) %*% t(X) %*% vc_y  # betaの推定
  
  f <- function(x) {
    S <- vc_beta[1] + vc_beta[2] * x + vc_beta[3] * x ^ 2 + vc_beta[4] * x ^ 3
    for (j in 1:p)
      S <- S + vc_beta[j + 4] * max((x - vc_knots[j]) ^ 3, 0)
    return(S)
  }  # 関数fを得る
  
  vc_x_seq <- seq(-5, 5, 0.02)

  if(k==1){
    df_spline <- data.frame(x = vc_x_seq,
                            col = paste0("区切り",vc_p_set[k],"個"),
                            y = as.vector(apply(data.frame(vc_x_seq),c(1,2),f)))
  }else{
    df_spline <- rbind(df_spline,data.frame(x = vc_x_seq,
                                            col = paste0("区切り",vc_p_set[k],"個"),
                                            y = as.vector(apply(data.frame(vc_x_seq),c(1,2),f))))
  }
}


df_test <- data.frame(x = vc_x,
                      col = "テストデータ",
                      y = vc_y)

g2 <- ggplot(data = df_test,mapping = aes(x = x, y = y, color = col)) + geom_point()
g2 <- g2 + geom_line(data = df_spline,mapping = aes(x = x, y = y, color = col))
g2 <- g2 + xlab(label = "X") + ylab(label = "Y")
g2 <- g2 + labs(color = "")
g2 <- g2 + scale_color_discrete(breaks = unique(df_spline$col))
g2 <- g2 + scale_x_continuous(limits = vc_x_seq[c(1,length(vc_x_seq))])
g2 <- g2 + theme_classic() + theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom",
                                 legend.title=element_text(size = 7),
                                 legend.text=element_text(size = 12),
                                 legend.background = element_blank())
g2 <- g2 + geom_hline(yintercept = 0, linetype = 3)

plot(g2)

6.4.2　Pythonによるシミュレーション例

##################
### 多項式回帰 ###
##################


import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib
import scipy
from scipy import stats
from numpy.random import randn
import copy

##########################
### テストデータの生成 ###
##########################
n = 100
x = randn(n)
y = np.sin(x) + randn(n)
m = 3
p_set = [3,5,7]
col_set = ['red','blue','green']


# 多項式の値を計算
def calc_polynomial(beta ,u):
    S = 0
    for j in range(len(beta)):
        S = S + beta[j] * u ** j
    return S

# グラフ化
plt.scatter(x, y, s = 20, c = 'black') # テストデータの描画
plt.ylim(-3, 3)
x_seq = np.arange(-3, 3, 0.1)

# 多項式を描画
for i in range(m):
    p = p_set[i] # 次数の設定
    
    X = np.ones([n,1])
    
    for j in range(1, p + 1):
        xx = np.array(x**j).reshape((n,1))
        X = np.hstack((X,xx))

    beta = np.linalg.inv(X.T @ X) @ X.T @ y
        
    def polynomial(u):
        return calc_polynomial(beta, u)
    plt.plot(x_seq, polynomial(x_seq), c = col_set[i], label = "p={}".format(p))
plt.legend(loc = 'lower left')

######################
### スプライン回帰 ###
######################

### テストデータの生成
n = 100
x = randn(n) * 2 * np.pi
y = np.sin(x) + randn(n)
col_set = ['red','blue','green']
K_set = [5,7,9]


plt.scatter(x, y, c = 'black', s = 10)
plt.xlim(-5,5)

for k in range(len(K_set)):
    K = K_set[k]
    knots = np.linspace(-2 * np.pi, 2 * np.pi, K)
    X = np.zeros((n, K + 4))
    
    # 行列Xの生成
    for i in range(n):
        X[i,0] = 1
        X[i,1] = x[i]
        X[i,2] = x[i] ** 2
        X[i,3] = x[i] ** 3
        for j in range(K):
            X[i, j + 4] = np.maximum((x[i] - knots[j])**3,0)
    beta = np.linalg.inv(X.T @ X) @ X.T @ y
    
    def calc_spline(x):
        S = beta[0] + beta[1] * x + beta[2] * x ** 2 + beta[3] * x ** 3
        for j in range(K):
            S=S+beta[j+4]*np.maximum((x-knots[j])**3,0)
        return S
    
    u_seq = np.arange(-5, 5, 0.02)
    v_seq = []
    for u in u_seq:
        v_seq.append(calc_spline(u))
    plt.plot(u_seq, v_seq, c = col_set[k], label = 'K={}'.format(K))
plt.legend()

次回

power-of-awareness.com

*1:実際には4次以上でも問題は無いものの、発散していくことから3次が丁度よい。

前回

6. 非線形回帰

6.1 多項式回帰

6.2 スプライン回帰

6.3 自然なスプライン関数への回帰

6.4 シミュレーション

6.4.1 Rによるシミュレーション例

6.4.2 Pythonによるシミュレーション例

次回